朴素贝叶斯代码实现python

Posted 2021-12-09 ZhangJiQun.

条件概率

 

朴素贝叶斯代码实现python 

​​​​​​机器学习之朴素贝叶斯算法详解_平原的博客-CSDN博客_朴素贝叶斯算法

一、 朴素贝叶斯
1、概率基础知识：
条件概率是指事件A在另外一个事件B已经发生条件下的发生概率。 条件概率表示为： P(A|B)， 读作“在B条件下A的概率”。
若只有两个事件A， B， 那么：
P ( A B ) = P ( A ∣ B ) P ( B ) = P ( B ∣ A ) P ( A ) P(AB) = P(A|B)P(B)=P(B|A)P(A)
P(AB)=P(A∣B)P(B)=P(B∣A)P(A)

P ( A ∣ B ) = P ( A B ) P ( B ) P(A|B) = \\frac{P(AB)}{P(B)}
P(A∣B)= 
P(B)
P(AB)
​    
 

那么：
P ( A ∣ B ) = P ( B ∣ A ) ∗ P ( A ) P ( B ) P(A|B) = \\frac{P(B|A)*P(A)}{P(B)}
P(A∣B)= 
P(B)
P(B∣A)∗P(A)
​    
 

全概率公式： 表示若事件A1，A2，…，An构成一个完备事件组且都有正概率，则对任意一个事件B都有公式成立。

P ( B ) = P ( A 1 B ) + P ( A 2 B ) + . . . + P ( A n B ) = ∑ P ( A i B ) = ∑ P ( B ∣ A i ) ∗ P ( A i )
P(B)=P(A1B)+P(A2B)+...+P(AnB)=∑P(AiB)=∑P(B|Ai)∗P(Ai)
P(B)=P(A1B)+P(A2B)+...+P(AnB)=∑P(AiB)=∑P(B|Ai)∗P(Ai)
P(B)
​    
  
=P(A 
1
​    
 B)+P(A 
2
​    
 B)+...+P(A 
n
​    
 B)
=∑P(A 
i
​    
 B)
=∑P(B∣A 
i
​    
 )∗P(A 
i
​    
 )
​    
 

贝叶斯公式是将全概率公式带入到条件概率公式当中， 对于事件Ak和事件B有：
P ( A k ∣ B ) = P ( B ∣ A k ) ∗ P ( A k ) ∑ P ( B ∣ A i ) ∗ P ( A i ) P(A_k|B)=\\frac{P(B|A_k)*P(A_k)}{\\sum{}P(B|A_i)*P(A_i)}
P(A 
k
​    
 ∣B)= 
∑P(B∣A 
i
​    
 )∗P(A 
i
​    
 )
P(B∣A 
k
​    
 )∗P(A 
k
​    
 )
​    
 

对于P ( A k ∣ B ) P(A_k|B)P(A 
k
​    
 ∣B)来说， 分母 ∑ P ( B ∣ A i ) ∗ P ( A i ) ∑P(B|A_i)*P(A_i)∑P(B∣A 
i
​    
 )∗P(A 
i
​    
 ) 为一个固定值， 因为我们只需要比较P ( A k ∣ B ) P(A_k|B)P(A 
k
​    
 ∣B)的大小，
所以可以将分母固定值去掉， 并不会影响结果。 因此， 可以得到下面公式：
P ( A k ∣ B ) = P ( A k ) ∗ P ( B ∣ A k ) P(A_k|B)=P(A_k)*P(B|A_k)
P(A 
k
​    
 ∣B)=P(A 
k
​    
 )∗P(B∣A 
k
​    
 )

$P(A_k) $先验概率， P ( A k ∣ B ) P(A_k|B)P(A 
k
​    
 ∣B) 后验概率， P ( B ∣ A k ) P(B|A_k)P(B∣A 
k
​    
 ) 似然函数
先验*似然=后验

 

 

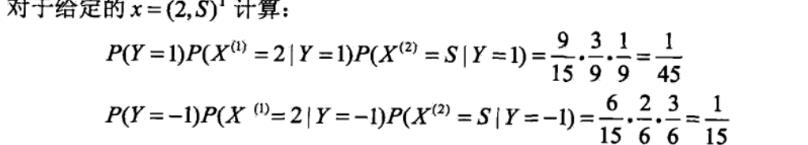
②三个阶段：
第一阶段——准备阶段， 根据具体情况确定特征属性， 对每个特征属性进行适当划分， 然后由人工对一部分待分类项进行分类，形成训练样本集合。这一阶段的输入是所有待分类数据，输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段， 其质量对整个过程将有重要影响，分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。

第二阶段——分类器训练阶段， 这个阶段的任务就是生成分类器，主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计， 并将结果记录。 其输入是特征属性和训练样本，输出是分类器。这一阶段是机械性阶段， 根据前面讨论的公式可以由程序自动计算完成。

第三阶段——应用阶段。 这个阶段的任务是使用分类器对待分类项进行分类， 其输入是分类器
和待分类项， 输出是待分类项与类别的映射关系。这一阶段也是机械性阶段， 由程序完成。

#coding:utf-8
# 极大似然估计  朴素贝叶斯算法
import pandas as pd
import numpy as np

class NaiveBayes(object):
    def getTrainSet(self):
        dataSet = pd.read_csv('naivebayes_data.csv')
        dataSetNP = np.array(dataSet)  #将数据由dataframe类型转换为数组类型
        trainData = dataSetNP[:,0:dataSetNP.shape[1]-1]   #训练数据x1,x2
        labels = dataSetNP[:,dataSetNP.shape[1]-1]        #训练数据所对应的所属类型Y
        return trainData, labels

    def classify(self, trainData, labels, features):
        #求labels中每个label的先验概率
        labels = list(labels)    #转换为list类型
        labels = list(labels)    #转换为list类型
        P_y = {}       #存入label的概率
        for label in labels:
            P_y[label] = labels.count(label)/float(len(labels))   # p = count(y) / count(Y)

        #求label与feature同时发生的概率
        P_xy = {}
        for y in P_y.keys():
            y_index = [i for i, label in enumerate(labels) if label == y]  # labels中出现y值的所有数值的下标索引
            for j in range(len(features)):      # features[0] 在trainData[:,0]中出现的值的所有下标索引
                x_index = [i for i, feature in enumerate(trainData[:,j]) if feature == features[j]]
                xy_count = len(set(x_index) & set(y_index))   # set(x_index)&set(y_index)列出两个表相同的元素
                pkey = str(features[j]) + '*' + str(y)
                P_xy[pkey] = xy_count / float(len(labels))

        #求条件概率
        P = {}
        for y in P_y.keys():
            for x in features:
                pkey = str(x) + '|' + str(y)
                P[pkey] = P_xy[str(x)+'*'+str(y)] / float(P_y[y])    #P[X1/Y] = P[X1Y]/P[Y]

        #求[2,'S']所属类别
        F = {}   #[2,'S']属于各个类别的概率
        for y in P_y:
            F[y] = P_y[y]
            for x in features:
                F[y] = F[y]*P[str(x)+'|'+str(y)]     #P[y/X] = P[X/y]*P[y]/P[X]，分母相等，比较分子即可，所以有F=P[X/y]*P[y]=P[x1/Y]*P[x2/Y]*P[y]

        features_label = max(F, key=F.get)  #概率最大值对应的类别
        return features_label


if __name__ == '__main__':
    nb = NaiveBayes()
    # 训练数据
    trainData, labels = nb.getTrainSet()
    # x1,x2
    features = [2,'S']
    # 该特征应属于哪一类
    result = nb.classify(trainData, labels, features)
    print (features,'属于',result)