实现二：BP算法实践|机器学习

Posted 桃陉

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了实现二：BP算法实践|机器学习相关的知识，希望对你有一定的参考价值。

目录

实验内容：实现BP算法类，并使用两个数据集进行测试。

BP算法（分步）

BP算法主要由前向传递和后向传递两个部分构成。

首先定义BPNetWork类：

初始化函数init，生成四个基本变量（权重+偏置）：

    '''初始化函数init'''
    def __init__(self,):
        '''
        w1、w2分别为输入层到隐藏层、隐藏层到输出层的权重；b1、b2分别为输入层到隐藏层、隐藏层到输出层的偏置；全部初始化为None
        '''
        self.w1 = None
        self.b1 = None
        self.w2 = None
        self.b2 = None

接下来就是BP算法的激活函数，还是选择使用sigmoid函数（S型函数）进行激活：

    '''激励函数sigmoid'''
    def sigmoid(self,X,):
        '''
        input:
            X(mat):转化前的值
        output：
            return(float):转化后的值
        '''
        return 1.0/(1+np.exp(-X))

激励函数sigmoid函数的导函数dsigmoid函数：

    '''激励函数sigmoid的导函数'''
    def dsigmoid(self,X):
        '''
        input:
            X(mat):转化前的值
        output：
            return(float):转化后的值
        '''
        m,n = np.shape(X)
        out = np.mat(np.zeros((m,n)))
        for i in range(m):
            for j in range(n):
                out[i,j] = self.sigmoid(X[i,j])*(1-self.sigmoid(X[i,j]))
        return out

接下来是前向传输的两步操作：输入层到隐藏层的计算、隐藏层到输出层的计算；

对于输入层到隐藏层的计算分为两步，第一步是输入矩阵与权重矩阵相乘，所得结果再加上该层对应的偏置值；第二步是使用sigmoid激励函数进行激励：

    '''隐藏层的hidden_in函数'''
    def hidden_in(self,X,):
        '''
        input:
            X(mat):输入层的输入矩阵
        output:
            return(mat):得到激励前的结果
        '''
        X = np.mat(X)
        m = np.shape(X)[0]
        hidden_input = X*self.w1
        for i in range(m):
            hidden_input[i,] += self.b1
        return hidden_input
    
    '''计算hidden_out结果'''
    def hidden_out(self,hidden_input):
        '''
        input:
            hidden_input(mat):激励前的mat
        output:
            return(mat):激励后的mat
        '''
        hidden_output = self.sigmoid(hidden_input)
        return hidden_output

对于隐藏层到输出层的计算分为两步，第一步是隐藏层的输出矩阵与权重矩阵相乘，所得结果再加上该层对应的偏置值；第二步是使用sigmoid激励函数进行激励：

    '''输出层的output_in函数'''
    def output_in(self,hidden_output,):
        '''
        input:
            hidden_output(mat):隐藏层的输出结果矩阵
        output:
            return(mat):输出层的输入矩阵
        '''
        hidden_output = np.mat(hidden_output)
        m = np.shape(hidden_output)[0]
        output_in = hidden_output*self.w2
        for i in range(m):
            output_in[i,] += self.b2
        return output_in
    
    '''计算output_out函数'''
    def output_out(self,output_in,):
         '''
        input:
            output_input(mat):输出层的输入结果矩阵
        output:
            return(mat):输出层的输出矩阵
        '''
        output_out = self.sigmoid(output_in)
        return output_out

总的前向传播函数forward为：

 '''前向传播函数forward'''
    def forward(self,X,):
        hidden_input = self.hidden_in(X)
        hidden_output = self.hidden_out(hidden_input)
        predict_in = self.output_in(hidden_output)
        predict_out = self.output_out(predict_in)
        return hidden_input,hidden_output,predict_in,predict_out

接下来是逆向传输调整权重以及偏置的fit函数（注意由于权重的取值为[-1,1]，所以进行如下操作生成随机的[-1,1]之间的数，之后再通过逆向传播进行优化权重）：

'''调整权重以及偏置的fit函数'''
    def fit(self,X,y,hiddens,outputs,lr=0.01,epochs=100):
        m,n = np.shape(X)
        
        self.w1 = np.mat(np.random.random((n,hiddens))*2-1)
        self.b1 = np.mat(np.zeros((1,hiddens)))
        self.w2 = np.mat(np.random.random((hiddens,outputs))*2-1)
        self.b2 = np.mat(np.zeros((1,outputs)))
        
        for epoch in range(epochs):
#             print("训练轮次：",epoch)
            hidden_input,hidden_output,predict_in,predict_out = self.forward(X)
            
            #反向传播
            #隐藏层到输出层之间的残差
            delta_output = -np.multiply((y-predict_out),self.dsigmoid(predict_in))
            #输入层到隐藏层之间的残差
            delta_hidden = np.multiply((delta_output*self.w2.T),self.dsigmoid(hidden_input))
            #更新权重与偏置，即梯度下降
            self.w2 = self.w2 -lr*(hidden_output.T*delta_output)#更新w1
            self.b2 = self.b2 - lr*np.sum(delta_output,axis=0)*(1.0/m)#更新b1
            self.w1 = self.w1 -lr*(X.T*delta_hidden)#更新w2
            self.b1 = self.b1 - lr*np.sum(delta_hidden,axis=0)*(1.0/m)#更新b0

最后是判断测试集准确率的预测函数predict:

'''预测函数predict'''
    def predict(self,x_test,):
        x_test = np.mat(x_test)
        hidden_input,hidden_output,predict_in,predict_out = self.forward(x_test)
        output = np.array(self.sigmoid(predict_out))
        return output

源代码（全部）

import numpy as np
from math import sqrt

class BPNetWork(object):
    
    '''初始化函数init'''
    def __init__(self,):
        '''
        w1、w2分别为输入层到隐藏层、隐藏层到输出层的权重；b1、b2分别为输入层到隐藏层、隐藏层到输出层的偏置；全部初始化为None
        '''
        self.w1 = None
        self.b1 = None
        self.w2 = None
        self.b2 = None
        
    '''激励函数sigmoid'''
    def sigmoid(self,X,):
        '''
        input:
            X(mat):转化前的值
        output：
            return(float):转化后的值
        '''
        return 1.0/(1+np.exp(-X))
    
    '''激励函数sigmoid的导函数'''
    def dsigmoid(self,X):
        '''
        input:
            X(mat):转化前的值
        output：
            return(float):转化后的值
        '''
        m,n = np.shape(X)
        out = np.mat(np.zeros((m,n)))
        for i in range(m):
            for j in range(n):
                out[i,j] = self.sigmoid(X[i,j])*(1-self.sigmoid(X[i,j]))
        return out
    
    '''隐藏层的输入函数'''
    def hidden_in(self,X,):
        X = np.mat(X)
        m = np.shape(X)[0]
        hidden_input = X*self.w1
        for i in range(m):
            hidden_input[i,] += self.b1
        return hidden_input
    
    '''隐藏层的输出函数'''
    def hidden_out(self,hidden_input,):
        hidden_output = self.sigmoid(hidden_input)
        return hidden_output
    
    '''输出层的输入函数'''
    def output_in(self,hidden_output,):
        hidden_output = np.mat(hidden_output)
        m = np.shape(hidden_output)[0]
        output_in = hidden_output*self.w2
        for i in range(m):
            output_in[i,] += self.b2
        return output_in
    
    '''输出层的输出函数'''
    def output_out(self,output_in):
        output_out = self.sigmoid(output_in)
        return output_out
    
    '''前向传播函数forward'''
    def forward(self,X,):
        hidden_input = self.hidden_in(X)
        hidden_output = self.hidden_out(hidden_input)
        predict_in = self.output_in(hidden_output)
        predict_out = self.output_out(predict_in)
        return hidden_input,hidden_output,predict_in,predict_out

    '''调整权重以及偏置的fit函数'''
    def fit(self,X,y,hiddens,outputs,lr=0.01,epochs=100):
        m,n = np.shape(X)
        
        self.w1 = np.mat(np.random.random((n,hiddens))*2-1)
        self.b1 = np.mat(np.zeros((1,hiddens)))
        self.w2 = np.mat(np.random.random((hiddens,outputs))*2-1)
        self.b2 = np.mat(np.zeros((1,outputs)))
        
        for epoch in range(epochs):
#             print("训练轮次：",epoch)
            hidden_input,hidden_output,predict_in,predict_out = self.forward(X)
            
            #反向传播
            #隐藏层到输出层之间的残差
            delta_output = -np.multiply((y-predict_out),self.dsigmoid(predict_in))
            #输入层到隐藏层之间的残差
            delta_hidden = np.multiply((delta_output*self.w2.T),self.dsigmoid(hidden_input))
            #更新权重与偏置，即梯度下降
            self.w2 = self.w2 -lr*(hidden_output.T*delta_output)#更新w1
            self.b2 = self.b2 - lr*np.sum(delta_output,axis=0)*(1.0/m)#更新b1
            self.w1 = self.w1 -lr*(X.T*delta_hidden)#更新w2
            self.b1 = self.b1 - lr*np.sum(delta_hidden,axis=0)*(1.0/m)#更新b0
        
    '''预测函数predict'''
    def predict(self,x_test,):
        x_test = np.mat(x_test)
        hidden_input,hidden_output,predict_in,predict_out = self.forward(x_test)
        output = np.array(self.sigmoid(predict_out))
        return output

测试数据集一（鸢尾花集）

首先我们导入鸢尾花数据集：

#导入数据集iris
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'class']  #特征属性
dataset = pandas.read_csv(url, names=names) #读取csv数据

我们可以看到数据集如下图所示：

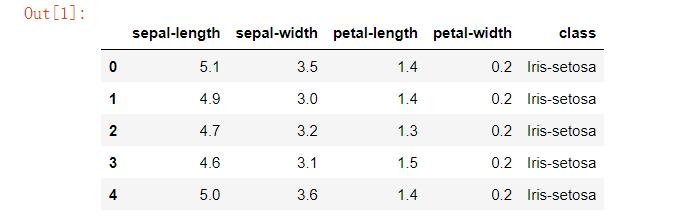
该数据集一共有150条数据，前四列为鸢尾花的特征属性，最后一列class为鸢尾花的标签，一共有三种Iris-setosa、Iris-versicolor、Iris-virginica，为了方便进行接下来的处理，我们需要分别把它们定义为0、1、2：

X = dataset.iloc[:,:-1].values  #取出特征属性
y = dataset.iloc[:,-1].values  #取出标签值

#转化标签为0、1、2
for i in range(len(y)):
    if y[i]=='Iris-setosa':
        y[i]=0
    elif y[i]=='Iris-versicolor':
        y[i]=1
    elif y[i]=='Iris-virginica':
        y[i]=2

但是注意到此时取出的标签y是1×150的行向量，为了运算我们需要把它转换为150×1的列向量。由于标签值为离散的0、1、2，为了处理的更加准确我们使用独热编码模型对标签值y进行独热编码，使其结果可以取连续的数，并转化为ndarry模型：

y = y.reshape(len(y),1)#改变y的形状
ohe = OneHotEncoder()#建立独热编码模型
y = ohe.fit_transform(y).toarray()#对标签值y进行独热编码，并转换为ndarray格式

接下来我们需要划分数据集为训练集和测试集，这里直接使用train_test_split方法进行处理，比例取4:1（即120条训练数据、30条测试数据）：

#划分训练集与测试集，参数test_size设为0.2，random_state设为666
x_train,x_test,y_train,y_test = train_test_split(X,y,test_size = 0.2,random_state = 666)

接下来就是最重要的一步，我们取BPNetWork类的实例bpNet，然后对其进行训练，取隐藏层结点为100个，输出层结点三个，学习率为0.01，最大迭代次数取200。训练结束后将测试集特征放入predict预测函数中得到结果，注意要将独热编码转换为原来的编码，然后预测数据与真实的测试数据结果进行对比得出模型训练准确率：

#模型实例，并训练
bpNet = BPNetWork()
bpNet.fit(x_train,y_train,100,3,0.01,200)

ypredict= bpNet.predict(x_test)
y_test = np.argmax(y_test,axis =1)
print("真实结果",y_test) #输出真实结果
p = np.argmax(ypredict,axis =1)#找到概率值最大的那个位置
print("预测结果",p)  #输出预测结果
acc = np.mean(p==y_test)
print('准确率为%.4f'%acc)

结果如下图所示：

迭代次数少的话会影响准确率，可以自行增加训练次数！

源代码（全部）

import pandas
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder

#导入数据集iris
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'class']
dataset = pandas.read_csv(url, names=names) #读取csv数据
dataset.head()
X = dataset.iloc[:,:-1].values
y = dataset.iloc[:,-1].values

for i in range(len(y)):
    if y[i]=='Iris-setosa':
        y[i]=0
    elif y[i]=='Iris-versicolor':
        y[i]=1
    elif y[i]=='Iris-virginica':
        y[i]=2

y = y.reshape(len(y),1)#改变y的形状
ohe = OneHotEncoder()#建立独热编码模型
y = ohe.fit_transform(y).toarray()#对标签值y进行独热编码，并转换为ndarray格式


#划分训练集与测试集，参数test_size设为0.2，random_state设为666
x_train,x_test,y_train,y_test = train_test_split(X,y,test_size = 0.2,random_state = 666)

bpNet = BPNetWork()
bpNet.fit(x_train,y_train,100,3,0.01,200)

ypredict= bpNet.predict(x_test)

y_test = np.argmax(y_test,axis =1)
print("真实结果",y_test)
p = np.argmax(ypredict,axis =1)#找到概率值最大的那个位置
print("预测结果",p)
acc = np.mean(p==y_test)
print('准确率为%.4f'%acc)

测试数据集二（手写数字集）

手写数据集的训练过程与鸢尾花集的训练过程叫基本相似，这里主要介绍它们之间不同的一些点。

手写数据集的获取过程：

# 加载手写数字数据集
digits = datasets.load_digits()
# 创建特征矩阵
feature = digits.data
# 创建目标向量
target = digits.target

该数据集的特征属性比较多，输出第一条数据的特征属性如下：

而它的目的是判断这些数据指向的是哪个数字，所以标签值就是0~9是个数字。

由于该数据集数据较多，我们这里只取了前200条进行处理，训练集与测试集的比例仍取4：1。

训练结果如下图所示：

源代码（全部）

from sklearn import datasets

# 加载手写数字数据集
digits = datasets机器学习——深度神经网络实践（FCNCNNBP）


 机器学习基础使用python实现BP算法


 吴恩达机器学习作业——BP神经网络--Python实现


 简单易学的机器学习算法——神经网络之BP神经网络


 基于matlab智能优化与机器学习结合算法数据预测清单


 数学建模MATLAB应用实战系列（106）-机器学习算法：BP神经网络（附MATLAB代码）