[海军国际项目办公室]CSP 2020
Posted StaroForgin
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[海军国际项目办公室]CSP 2020相关的知识,希望对你有一定的参考价值。
CSP 2020
题目概述

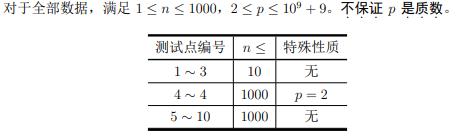
题解
为什么会有人取这么奇怪的题目名。
首先,我们可以通过 打表 简单推理发现一个性质,在较大的
n
n
n下,我们真正答案的长度与
n
3
n^3
n3所能构成的最短的字符串的长度相近。
事实上也很好证明,因为我们是将
n
3
n^3
n3分解得到第
n
4
n^4
n4小的数,最短的字符串可能由于刚好挤满,所以不能排到
n
4
n^4
n4,但如果刚好比最短的字符串长度大一,就完完全全可以排到第
n
4
n^4
n4小的数了。
所以我们可以先判断一下我们答案的字符串长度,只可能是
⌈
n
3
9
⌉
\\lceil\\frac{n^3}{9}\\rceil
⌈9n3⌉或者
⌈
n
3
9
⌉
+
1
\\lceil\\frac{n^3}{9}\\rceil+1
⌈9n3⌉+1。
而由于我们的长度与最短长度非常接近,所以事实上我们的该字符串中绝大部分位置都是
9
9
9。
我们记我们的答案字符串为
a
a
a,事实上
∑
(
9
−
a
)
⩽
14
\\sum (9-a)\\leqslant 14
∑(9−a)⩽14,也就是说我们从一个全是
9
9
9的串中,减去不超过
13
13
13个
1
0
x
10^x
10x就可以得到我们的答案。
我们可以用二分的方法,找到我们那即为需要减,将其减去。
但如果要二分的话,我们相当于要知道比我们在
x
x
x这位减一个
1
1
1要小的方法的数量。
显然,如果要比这样减小,那肯定是在
x
x
x这位前面减了一个
1
1
1,方法数很容易求出。
我们记
g
(
x
,
y
)
g(x,y)
g(x,y)表示在一个长度为
y
y
y的全是
9
9
9的串中,选出
y
y
y个
1
1
1减的方法数。
前面的方案可以有
g
g
g差分得出,我们只需要从随便选中减去一个大于
x
x
x都不选的方法即可,也就是
g
(
n
,
y
)
−
g
(
x
,
y
)
g(n,y)-g(x,y)
g(n,y)−g(x,y)。
但我们的
g
g
g函数又可以怎么求呢?
其实这东西的求法应该很容易联想到我们的斯特林反演,但是我们在每一位上都不能选择超过
9
9
9个,所以还得改改,我们记
d
p
i
,
j
dp_{i,j}
dpi,j就是在一个长度为
i
i
i的全是
9
9
9的串中,每一位至少被选择一个,总共选择
j
j
j个的方法数。
容易得到
d
p
dp
dp转移式,
d
p
i
,
j
=
∑
k
=
1
min
(
9
,
j
)
d
p
i
−
1
,
j
−
k
dp_{i,j}=\\sum_{k=1}^{\\min(9,j)dp_{i-1,j-k}}
dpi,j=∑k=1min(9,j)dpi−1,j−k。
显然,我们可以知道,
g
(
x
,
y
)
=
∑
i
=
0
min
(
x
,
y
)
(
x
i
)
d
p
i
,
y
g(x,y)=\\sum_{i=0}^{\\min(x,y)}\\binom{x}{i}dp_{i,y}
g(x,y)=i=0∑min(x,y)(ix)dpi,y接下来,我们只需要在原数中找到那些为我们要减去,枚举它们要减去多少位就可以了。
实际上真正需要减去的位上的数量也是比较少的。
我们对于
[
5
,
n
]
[5,n]
[5,n]中每个数都这样跑一次就行了,较小的
[
1
,
4
]
[1,4]
[1,4]部分可以打表。
时间复杂度
O
(
n
l
o
g
n
)
O\\left(nlog\\,n\\right)
O(nlogn),但常数可能不太小。
不过跑得还是很快,只要
111
m
s
111ms
111ms。
源码
#include<bits/stdc++.h>
using namespace std;
#define MAXN 1005
#define lowbit(x) (x&-x)
#define reg register
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
typedef long long LL;
typedef unsigned long long uLL;
const int INF=0x3f3f3f3f;
const int mo=998244353;
const int inv2=499122177;
const double jzm=0.997;
const int zero=10000;
const int orG=3,invG=332748118;
const LL lim=1e18+1LL;
const double Pi=acos(-1.0);
const double eps=1e-5;
typedef pair<LL,int> pii;
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){
_T f=1;x=0;char s=getchar();
while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}
while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
x*=f;
}
template<typename _T>
void print(_T x){if(x<0){x=(~x)+1;putchar('-');}if(x>9)print(x/10);putchar(x%10+'0');}
int gcd(int a,int b){return !b?a:gcd(b,a%b);}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,LL s,int p){int t=1;while(s){if(s&1LL)t=1ll*a*t%p;a=1ll*a*a%p;s>>=1LL;}return t;}
LL n,p,dp[20][20],pw9[40];
LL mul(LL x,LL y){return (x&&lim/x<y)?lim:min(x*y,lim);}
LL C(int x,int y){
LL res=1;
for(int i=x;i>x-y&&res!=lim;i--)res=mul(res,1ll*i);
if(res==lim)return res;
for(int i=1;i<=y;i++)res/=1ll*i;
return res;
}
LL work(int x,int y){
LL res=0,sum=1;
for(int i=0;i<=min(x,y)&&res!=lim;i++){
res=min(res+mul(sum,dp[y][i]),lim);
sum=mul(sum,x-i);sum/=1ll*(i+1);
}
return res;
}
LL sakura(int len,int num,LL sum,int up){
if(!num)return 0;
for(int i=min(up,num);i>0;i--){
LL tmp=work(len-1,num-i);
if(sum<=tmp)return add(1ll*i*qkpow(10,len-1,p)%p,sakura(len-1,num-i,sum,9),p);
sum-=tmp;
}
LL all=work(len-1,num);int l=1,r=len-1;
while(l<r){
int mid=l+r>>1;LL tmp=all-work(mid,num);
if(tmp<sum)r=mid;else l=mid+1;
}
LL tmp=all-work(l,num);
return add(qkpow(10,l-1,p),sakura(l,num-1,sum-tmp,8),p);
}
signed main(){
freopen("number.in","r",stdin);
freopen("number.out","w",stdout);
read(n