1356. 回文质数难度: 中 / 数学

Posted 2021-12-09 辉小歌

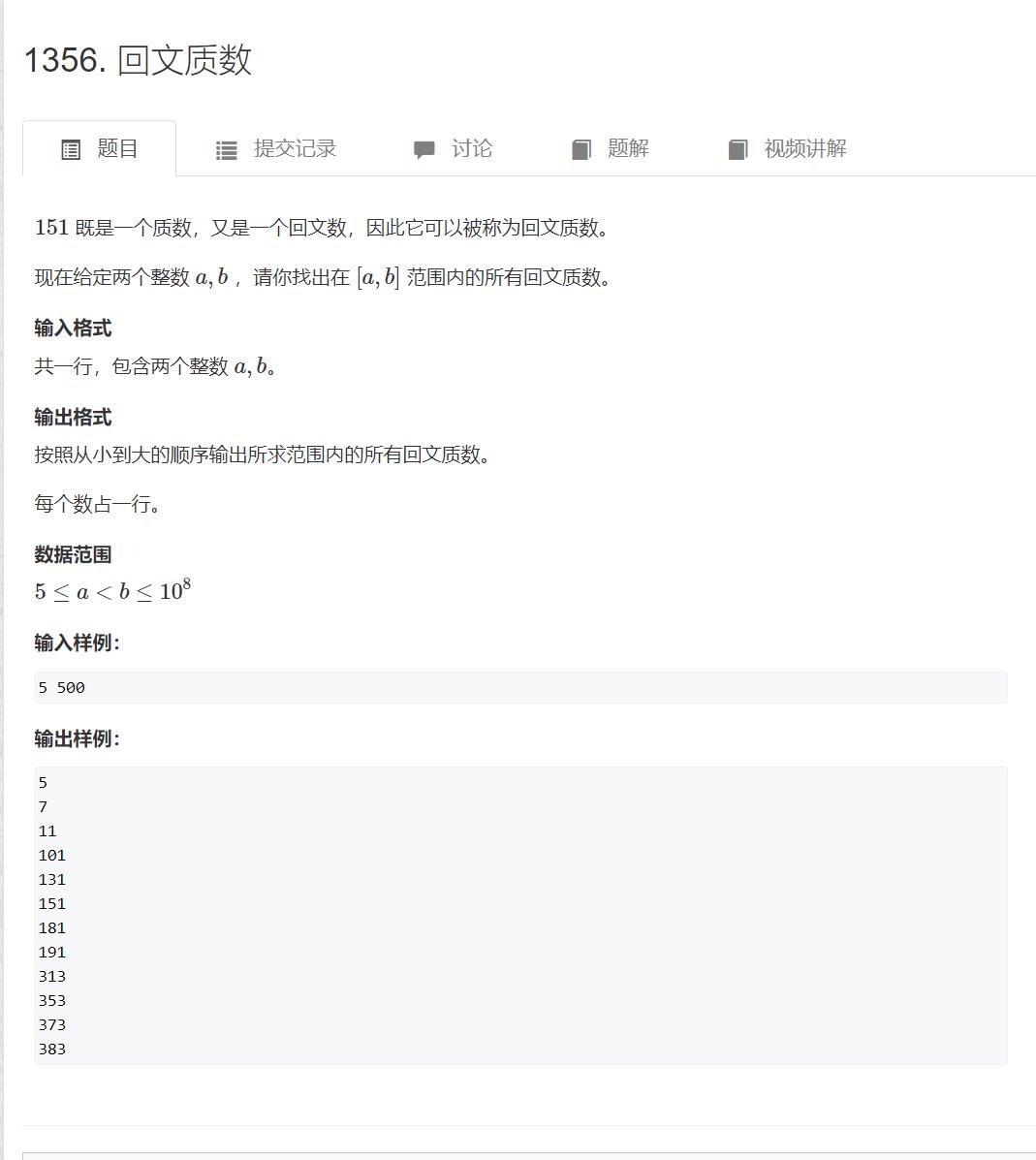
https://www.acwing.com/problem/content/description/1358/
数据范围很大我们需要优化。
首先要了解的知识点:

• 9/3 的倍数：各位数字之和能被3整除
• 2/5的倍数: 个位数字能被2/5整除
• 4的倍数: 后两位能被4整除
• 8的倍数: 后三位能被8整除
• 11 的倍数: 奇数位的和 和 偶数位的和的差能被11整除

我们这里就用到了11的倍数的性质。首先1e8一定是一个合数直接排除。
我们看1000,0000 - 9999,9999 我们知道的是一个回文串左右对称，故奇数位的和 和 偶数位的和的差==0 一定能被11整除 即一定是11的倍数。
故我们只需考虑[5,1e7)内的质数即可。

#include<bits/stdc++.h>
using namespace std;
const int N=1e7+10;
int prime[N],st[N],cnt;
void init()
{
    int n=1e7; 
    for(int i=2;i<=n;i++)
    {
        if(!st[i]) prime[cnt++]=i;
        for(int j=0;prime[j]<=n/i;j++)
        {
            st[i*prime[j]]=1;
            if(i%prime[j]==0) break;
        }
    }
}
bool check(int x)
{
    string a=to_string(x);
    string b=a;
    reverse(b.begin(),b.end());
    return a==b;
}
int main(void)
{
    init();
    int st,ed; cin>>st>>ed;
    for(int i=0;i<cnt;i++)
    {
        if(prime[i]>=st&&prime[i]<=ed)
        {
            if(check(prime[i])) printf("%d\\n",prime[i]);
        }
        else if(prime[i]>ed) break;
    }
    return 0;
}