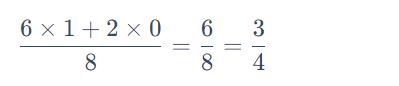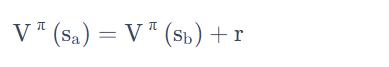DQN笔记:MC & TD
Posted UQI-LIUWJ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了DQN笔记:MC & TD相关的知识,希望对你有一定的参考价值。
1 前言
传统的强化学习算法会使用表格的形式存储状态值函数 V(s)或状态动作值函数 Q(s,a),但是这样的方法存在很大的局限性。【强化学习笔记:Q-learning_UQI-LIUWJ的博客-CSDN博客】
现实中的强化学习任务所面临的状态空间往往是连续的,存在无穷多个状态,在这种情况下,就不能再使用表格对值函数进行存储。
在 Q-learning 中,我们使用表格来存储每个状态 s 下采取动作 a 获得的奖励,即状态-动作值函数 Q(s,a)。然而,这种方法在状态量巨大甚至是连续的任务中,会遇到维度灾难问题,往往是不可行的。因此,DQN 采用了价值函数近似的表示方法。
为了在连续的状态和动作空间中计算值函数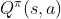 ,我们可以用一个函数
,我们可以用一个函数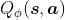 来表示近似计算,称为
来表示近似计算,称为价值函数近似(Value Function Approximation)。
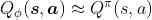
其中
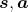 分别是状态 s 和动作 a 的向量表示,
分别是状态 s 和动作 a 的向量表示,- 函数
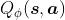 通常是一个参数为 ϕ 的函数,比如
通常是一个参数为 ϕ 的函数,比如神经网络,输出为一个实数,称为Q 网络(Q-network)。 - 模型中,也可以不使用Q(s,a),使用V(s)也可以
2 衡量价值函数
怎么衡量这个状态价值函数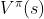 呢?有两种不同的做法:MC-based 的方法和 TD-based 的方法。
呢?有两种不同的做法:MC-based 的方法和 TD-based 的方法。
整体上和Q-learning 的类似
强化学习笔记:Q-learning_UQI-LIUWJ的博客-CSDN博客
强化学习笔记:Q-learning :temporal difference 方法_UQI-LIUWJ的博客-CSDN博客
2.1 MC
Monte-Carlo(MC)-based的方法就是去跟环境做互动,估计对于某一个策略,看到各个状态的时候的累计奖励。
但是实际上,我们不可能把所有的状态通通都扫过,但是没有关系。 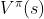 是一个网络。对一个网络来说,就算输入状态是从来都没有看过的,它也可以想办法估测一个值。
是一个网络。对一个网络来说,就算输入状态是从来都没有看过的,它也可以想办法估测一个值。
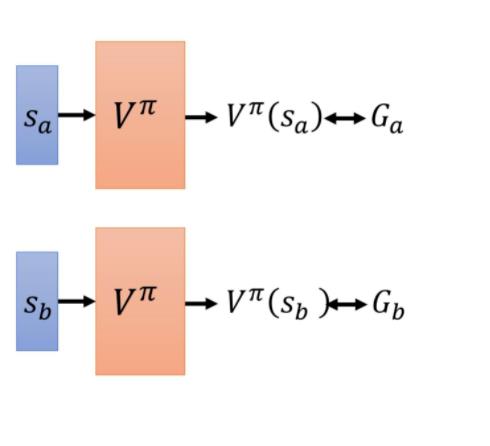
怎么训练这个网络呢?因为如果在状态sa,接下来的累积奖励就是Ga(采样中episode出现sa的取平均)。也就是说,对这个价值函数来说,如果输入是状态 sa,正确的输出应该是Ga。如果输入状态 sb,正确的输出应该是值Gb。
所以在训练的时候, 它就是一个 回归问题。网络的输出就是一个值,你希望在输入sa 的时候,输出的值跟 Ga 越近越好,输入sb 的时候,输出的值跟Gb 越近越好。接下来把网络训练下去,就结束了。这是 MC-based 的方法。
2.2 TD(temporal difference 时序差分)
在 MC-based 的方法中,每次我们都要算累积奖励,也就是从某一个状态sa 一直玩到游戏结束的时候,得到的所有奖励的总和。
所以要使用 MC-based 的方法,你必须至少把这个游戏玩到结束。但有些游戏非常长,你要玩到游戏结束才能够更新网络,花的时间太长了,因此我们会采用 TD-based 的方法。
TD-based 的方法不需要把游戏玩到底,只要在游戏的某一个情况,某一个状态 的时候,采取动作
的时候,采取动作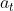 得到奖励
得到奖励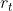 ,跳到状态
,跳到状态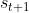 ,就可以使用 TD 的方法。
,就可以使用 TD 的方法。
TD基于以下这个式子:
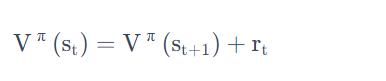
假设我们现在用的是某一个策略 π,在状态 ,它会采取动作
,它会采取动作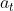 ,给我们奖励
,给我们奖励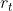 ,接下来进入
,接下来进入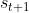 。状态
。状态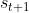 的值跟状态
的值跟状态 的值,它们的中间差了一项
的值,它们的中间差了一项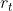 。你把
。你把 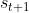 得到的值加上得到的奖励
得到的值加上得到的奖励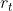 就会等于
就会等于 得到的值。
得到的值。
有了这个式子以后,你在训练的时候,你并不是直接去估测 V,而是希望你得到的结果 V 可以满足这个式子。
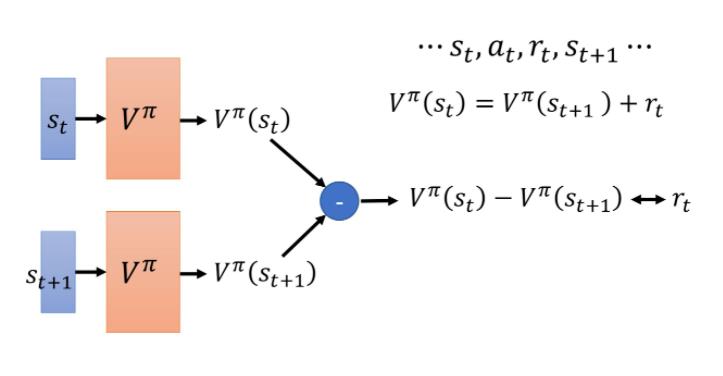
也就是说我们会是这样训练的,我们把 丢到网络里面,因为
丢到网络里面,因为 丢到网络里面会得到
丢到网络里面会得到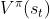 ,把
,把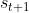 丢到你的值网络里面会得到
丢到你的值网络里面会得到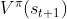 ,这个式子告诉我们,
,这个式子告诉我们,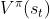 减
减 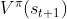 的值应该是
的值应该是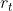 。
。
然后希望它们两个相减的 loss 跟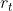 越接近,以这个作为目标函数训练下去,更新 V 的参数,你就可以把 V 函数学习出来。
越接近,以这个作为目标函数训练下去,更新 V 的参数,你就可以把 V 函数学习出来。
3 MC和TD的区别
MC 最大的问题就是方差很大。因为我们在玩游戏的时候,它本身是有随机性的。所以你可以把 Ga 看成一个随机变量。因为你每次同样走到sa 的时候,最后你得到的路径episode是不一样的,因而得到的Ga也是不一样的。(每一次得到 Ga 的差别其实会很大)
如果用 TD 的话,你是要去最小化这样的一个式子:
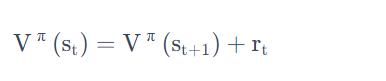
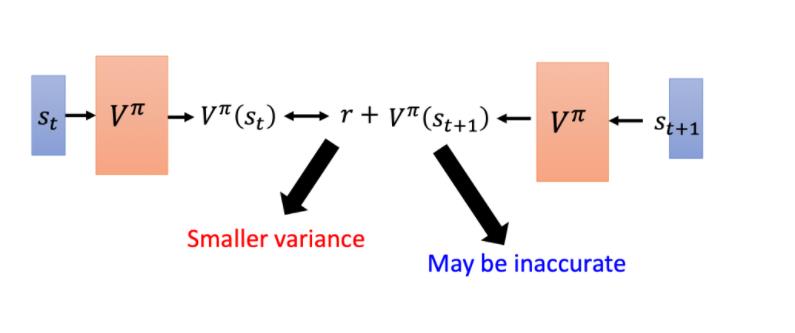
在这中间会有随机性的是 r。因为计算你在 st 采取同一个动作,你得到的奖励也不一定是一样的,所以 r 是一个随机变量。[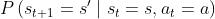 ,同一个状态同一个action,有不同概率进图不同的后续状态]
,同一个状态同一个action,有不同概率进图不同的后续状态]
但这个随机变量的方差会比 Ga 还要小,因为 Ga 是很多 r 合起来,这边只是某一个 r 而已。
但是这边你会遇到的一个问题是你这个 V 不一定估得准。假设你的这个 V 估得是不准的,那你使用这个式子学习出来的结果,其实也会是不准的。
所以 MC 跟 TD 各有优劣。今天 TD 的方法是比较常见的,MC 的方法是比较少用的。
4 举例说明MC和TD的区别

有一个策略π 跟环境互动了8 次,得到了8 次结果。
我们先计算 sb 的值。 状态 sb 在 8 场游戏里面都有经历过,其中有 6 场得到奖励 1,有 2 场得到奖励 0。所以如果你是要算期望值的话,就算看到状态sb 以后得到的奖励,一直到游戏结束的时候得到的累积奖励期望值是 3/4,计算过程如下式所示:
那Sa的奖励怎么计算呢?
假如用 MC 的话,你会发现这个sa 就出现一次,看到sa 这个状态,接下来累积奖励就是 0,所以 sa 期望奖励就是 0。
但 TD 在计算的时候,它要更新下面这个式子:
因为我们在状态 a 得到奖励 r=0 以后,跳到状态sb。
所以状态 sa 的奖励会等于状态sb 的奖励加上在状态 sa 跳到状态 sb 的时候可能得到的奖励 r。
而这个得到的奖励 r 的值是 0,sb 期望奖励是 3/4,那 sa 的奖励应该是 3/4。
用 MC 跟 TD 估出来的结果很有可能是不一样的。也就是说,就算观察到一样的训练数据,它最后估出来的结果也不一定是一样的。为什么会这样呢?换句话说,哪一个结果比较对呢?其实就都对。
在第一个轨迹, sa 得到奖励 0 以后,再跳到 sb 也得到奖励 0。这边有两个可能:
-
一个可能是: sa 是一个标志性的状态,只要看到 sa 以后,sb 就会拿不到奖励,sa 可能影响了sb。如果是用 MC 的算法的话,它会把sa 影响 sb 这件事考虑进去。所以看到sa 以后,接下来 sb 就得不到奖励,所以s_a期望的奖励是 0。
-
另一个可能是:看到 sa 以后,sb 的奖励是 0 这件事只是一个巧合,并不是 sa 所造成,而是因为说 sb 有时候就是会得到奖励 0,这只是单纯运气的问题。其实平常 sb 会得到奖励期望值是 3/4,跟 sa 是完全没有关系的。所以假设 sa 之后会跳到 s_bsb,那其实得到的奖励按照 TD 来算应该是 3/4。所以s_a期望的奖励是 3/4。
所以不同的方法考虑了不同的假设,运算结果不同。
以上是关于DQN笔记:MC & TD的主要内容,如果未能解决你的问题,请参考以下文章