AI数学用梯度下降算法优化线性回归方程（含代码）

Posted 2021-12-08 木盏

众所周知，线性回归（Linear Regression）是最常见的机器学习算法之一，简单但超级实用。线性回归旨在用线性方程来拟合数据分布，在数据量小计算速度要求高的地方是神经网络的最佳替代品。
LR的一般表现形式为：$y={\vec{w}}^T\vec{x}+b$
通常，LR优化方式可以通过构建均方误差损失函数，得到一个凸函数，计算导数为0的位置来确定$\vec{w}$和$b$，如周志华老师西瓜书里描述的那样。
在工程上，我们可以把LR当做一个简易的神经网络来对待，用梯度下降算法就可以优化。本文提供一个梯度下降算法优化LR的实验例子，有助于加深大家对LR以及梯度下降的理解。

实验意图：

假设有一个绝对正确的函数$y=f(\vec{x};\vec{w},b)={\vec{w}}^T\vec{x}+b$，每输入一个$\vec{x}$都可以得到一个准确的$y$。那么，咱们只需要得到最真实的$\vec{w}$和$b$即可。假设最真实的$\vec{w}=[3,1,4,1,5,9,2,6]$，最真实的$b=3.7$。
初始化$\vec{w}$和$b$为随机数，通过大量样本的梯度反传来修正$\vec{w}$和$b$到真实的值。
推导过程：

---

实验环境:

python3.7
numpy >=1.15.1

先申明，以下代码为本人原创，借用最好在评论中告知我。

########################################################
# @author: MuZhan
# @contact: [e-mail]
# experiment: using GD to optimize Linear Regression
# To fit `y=w*x+b`, where x and w are multi-dim vectors.
########################################################
import numpy as np

# initial setting
np.random.seed(10)
epochs = 30
lr = .1 # learning rate
w_ = np.array([3, 1, 4, 1, 5, 9, 2, 6]) # the ground truth w
b_ = 3.7 # the ground truth b
SAMPLE_NUM = 100
x_dim = len(w_)


# preparing random (x, y) pairs
print('preparing data...')
x_list = []
y_list = []
for i in range(SAMPLE_NUM):
    x = np.random.rand(x_dim)
    y = w_.dot(x) + b_ 
    x_list.append(x)
    y_list.append(y)

# init w
np.random.seed(10)
w = np.random.rand(x_dim)

# init b
b = 1

# training
print('training...')
for e in range(epochs):
    print('epoch: ', e, end='\\t')
    sum_loss = 0
    for i in range(len(x_list)):
        x = x_list[i]
        y_ = y_list[i]
        y = w.dot(x) + b
        loss = (y - y_) ** 2
        sum_loss += loss

        # use Gradient Descent to update parameters
        w = w - 2 * lr * (y - y_) * x
        b = b - 2 * lr * (y - y_)
    print('loss: ', sum_loss)

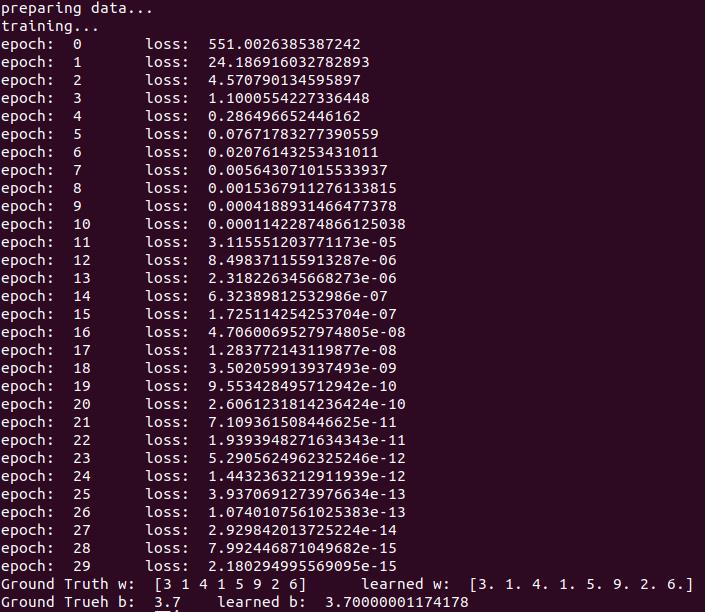
print('Ground Truth w: ', w_, end='\\t')
print('learned w: ', w)
print('Ground Trueh b: ', b_, end='\\t')
print('learned b: ', b)

c++:

#include<iostream>
#include<vector>
#include<cstdlib>
#define SAMPLES_NUM 10000
#define EPOCHS 20
#define LEARNING_RATE 0.001

using namespace std;

float dot(float* x, float* w, int length){
    float res = 0;
    for(int i=0; i<length; ++i){
        res += x[i] * w[i];
    }
    return res;
}

float get_random(){
    return (rand() % 1000) / 100.0;
}

void update_weights(float* x, float* w, int length, float sqrt_loss)
{
	for(int i=0; i<length; ++i){
	    w[i] -= 2 * LEARNING_RATE * sqrt_loss * x[i];
	}
}


int main(){
    float x[8] = {1, 1, 2, 2, 3, 3, 4, 4};
    float w_[8] = {3, 1, 4, 1, 5, 9, 2, 6}; // Ground Truth w
    float b_ = 3.7; // Ground Truth b
    int length = int(sizeof(w_)/sizeof(w_[0]));
    float y;

    // collect samples
    vector<vector<float>> samples;
    vector<float> tmp;
    for(int i=0; i<=length; ++i) tmp.push_back(0);
    for(int i=0; i<SAMPLES_NUM; ++i){
        for(int j=0; j<length; ++j){
	    tmp[j] = get_random();
	    x[j] = tmp[j];
	}
	y = dot(x, w_, length) + b_;
	tmp[length] = y;
        samples.push_back(tmp);
    }

    // init w, b
    float w[8] = {1, 2, 3};
    float b = 1.0f;


    // training
    float x_tmp[length];
    float y_tmp, loss;
    for(int e=0; e<EPOCHS; ++e){
        for(int i=0; i<samples.size(); ++i){
	    vector<float> sample = samples[i];
	    copy(sample.begin(), sample.end(), x_tmp);
	    y_tmp = sample[length];
	    y = dot(x_tmp, w, length) + b;
	    loss = (y - y_tmp) * (y - y_tmp);

	    // update parameters
	    update_weights(x_tmp, w, length, (y - y_tmp));
	    b -= 2 * LEARNING_RATE * (y - y_tmp);
            
	}
	    cout<<loss<<endl;
    }
    for(int i=0; i<length; ++i){
        cout<<w[i]<<" ";
    }
    cout<<endl;
    cout<<b<<endl;

    return 0;
}