《算法零基础》第18讲：线性枚举- 统计法入门

Posted 2021-12-08 Sauron7i

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了《算法零基础》第18讲：线性枚举- 统计法入门相关的知识，希望对你有一定的参考价值。

前言

原文章：线性枚举(二) - 统计法入门

概念

线性枚举中，一个很常用的算法就是对数组中的元素进行统计，比如 : 统计数组中的奇数的个数、统计数组中是5的倍数的数的个数，方法都是类似，需要对数组进行遍历枚举，然后根据题目条件做相应的判断，条件满足则计入统计，计数器加一。

LeetCode 1295. 统计位数为偶数的数字

原题链接：1295. 统计位数为偶数的数字

代码

class Solution {
public:

    bool IsEvenBit(int n)
    {
        int ans = 0;
        while (n)
        {
            n /= 10;
            ++ans;
        }
        return (ans % 2 == 0);
    }
    int findNumbers(vector<int>& nums)
    {
        int count = 0;
        for (int i = 0; i < nums.size(); ++i)
        {
            if (IsEvenBit(nums[i]))
            {
                ++count;
            }
        }
        return count;
    }
};

540. 有序数组中的单一元素

原题链接：540. 有序数组中的单一元素

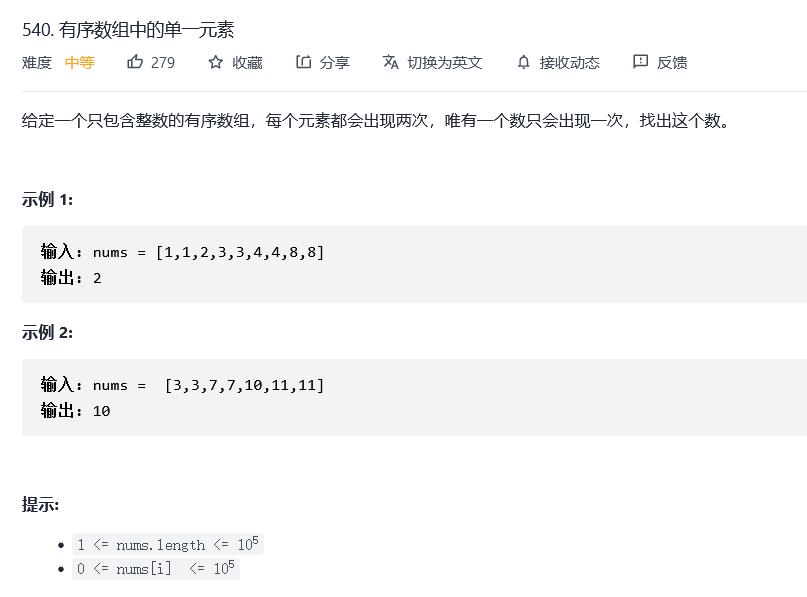
分析

方法一：
因为数组是有序的，所以我们直接遍历一遍，每次让条件 i+2，如果nums[i] 不等于nums[i + 1]，就找到了唯一元素。

方法二：
位运算：异或
因为一个数据对同一个数据异或两次，最终结果不变。

方法1

int singleNonDuplicate(int* nums, int numsSize)
{
   if (numsSize < 2)
   {
       return nums[0];
   }

   for (int i = 0; i < numsSize - 1; i += 2)
   {
       if (nums[i] != nums[i + 1])
       {
           return nums[i];
       }
   }
    return nums[numsSize - 1];
}

方法二

int singleNonDuplicate(int* nums, int numsSize)
{
    int ans = 0;
   for (int i = 0; i < numsSize; ++i)
   {
       ans ^= nums[i];
   }
    return ans;
}

剑指 Offer 21. 调整数组顺序使奇数位于偶数前面

原题链接：剑指 Offer 21. 调整数组顺序使奇数位于偶数前面

方法1：首尾双指针


 void Swap(int* a, int* b)
 {
     int temp = *a;
     *a = *b;
     *b = temp;
 }
int* exchange(int* nums, int numsSize, int* returnSize)
{
   int left = 0;
   int right = numsSize - 1;

   while(left < right)
   {
       if ((nums[left] & 1) == 1)
       {
           left++;
           continue;
       }
       if ((nums[right] & 1) == 0)
       {
           right--;
           continue;
       }
       Swap(&nums[left], &nums[right]);
   }

   *returnSize = numsSize;
   return nums;
}

方法2：快慢指针

 void Swap(int* a, int* b)
 {
     int temp = *a;
     *a = *b;
     *b = temp;
 }
int* exchange(int* nums, int numsSize, int* returnSize)
{
    int fast = 0;
    int low = 0;

    while (fast < numsSize)
    {
        if ((nums[fast] & 1) == 1)
        {
            Swap(&nums[low], &nums[fast]);
            low++;
        }
        fast++;
    }

    *returnSize = numsSize;
    return nums;
}

1991. 找到数组的中间位置

原题链接：1991. 找到数组的中间位置

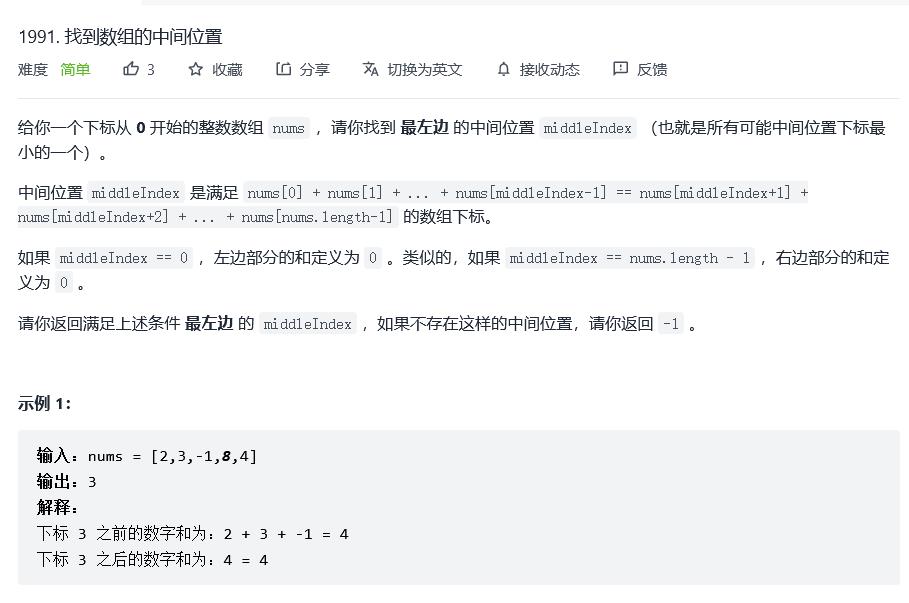
分析

若要保证中间位置左右两边元素和相等。
那就需要一个等式：

左边和 + 右边和 + 中间位置值 = 总元素和

那如果要找到准确的中间位置，又需要
左边和 == 右边和

因此可推出公式

左边和 * 2 + 中间位置值 = 总元素和

代码

int findMiddleIndex(int* nums, int numsSize)
{
    if (NULL == nums) return -1;

    int sum = 0;
    for (int i = 0; i < numsSize; ++i)
    {
        sum += nums[i];
    }

    int leftsum = 0;
    for (int i = 0; i < numsSize; ++i)
    {
        if (leftsum*2 + nums[i] == sum)
        {
            return i;
        }
        leftsum += nums[i];
    }

    return -1;
}

724. 寻找数组的中心下标

原题链接：724. 寻找数组的中心下标

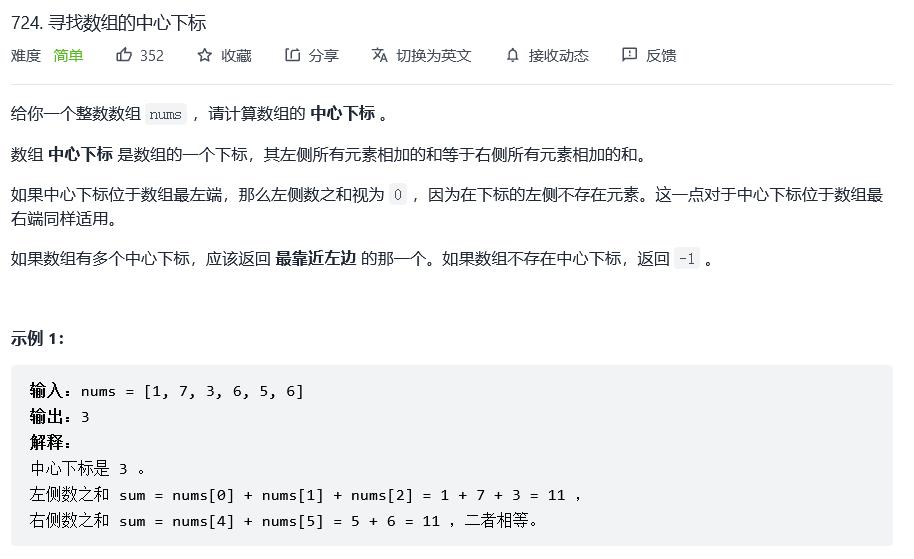
代码

和上个题一样的

int pivotIndex(int* nums, int numsSize)
{
    int total = 0;
    //总和
    for (int i = 0; i < numsSize; ++i)
    {
        total += nums[i];
    }

    int sum = 0;
    //total == nums[i] + sum + sum;
    for (int i = 0; i < numsSize; ++i)
    {
        if (total - nums[i] == sum * 2)
        {
            return i;
        }
        sum += nums[i];
    }
    return -1;
}

26. 删除有序数组中的重复项

原题链接：26. 删除有序数组中的重复项

分析

根据题目要求，原地修改数组，返回修改后的长度。

代码

方法很妙

int removeDuplicates(int* nums, int numsSize)
{
    if (numsSize < 2)
    {
        return numsSize;
    }

    int n = 0;
    
    for (int i = 1; i < numsSize; ++i)
    {
        if (nums[n] != nums[i])
        {
            nums[++n] = nums[i];
        }
    }

    return n + 1;
}

1018. 可被 5 整除的二进制前缀

原题链接：1018. 可被 5 整除的二进制前缀

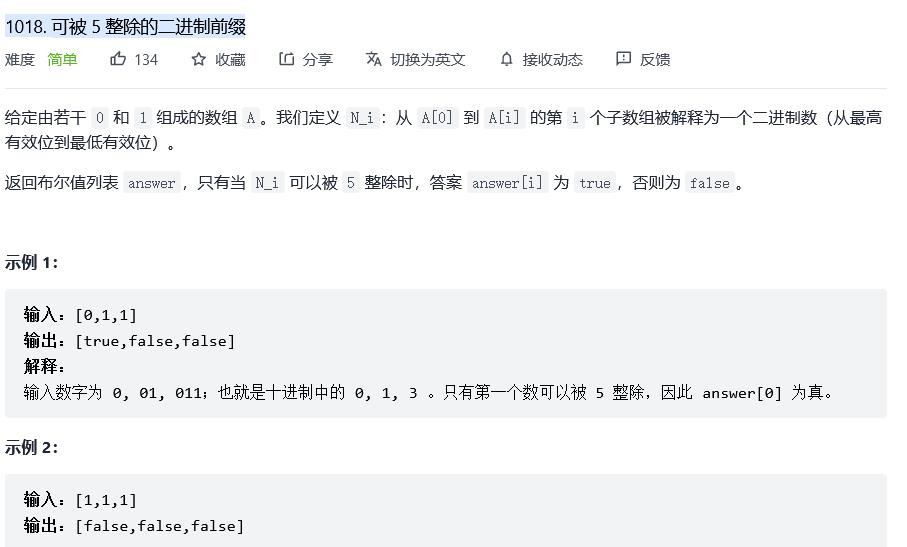
分析

注：图片来自力扣

代码


bool* prefixesDivBy5(int* nums, int numsSize, int* returnSize)
{
    *returnSize = numsSize;
    if (nums == NULL) return NULL;

    bool* ans = (bool*)malloc(sizeof(bool) * numsSize);

    int tmp = 0;
    for (int i = 0; i < numsSize; ++i)
    {
        tmp = ((tmp << 1) + nums[i]) % 5;
        
        ans[i] = tmp == 0;
    }

    return ans;
}

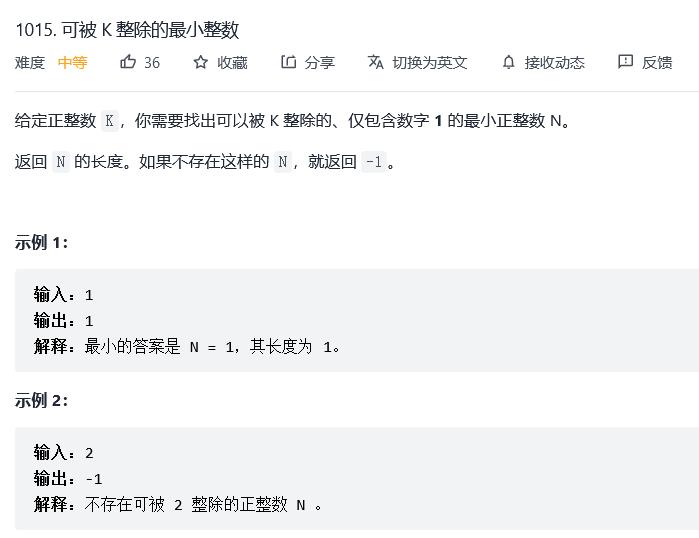
1015. 可被 K 整除的最小整数

原题链接：1015. 可被 K 整除的最小整数

代码

int smallestRepunitDivByK(int k)
{
    if (k % 2 == 0 || k % 5 == 0)
        return -1;
    
    int i = 1;
    for (int n = 1; n % k != 0; ++i)
    {
        n %= k;
        n = n * 10 + 1;
    }

    return i;
}