networkx图论Kruskal Algorithm最小生成树，Python

Posted 2021-12-08 zhangphil

Kruskal Algorithm和Prim最大的差异是Kruskal Algorithm是基于权边的。Kruskal Algorithm以权边维度，不断迭代加边（最小权边）。Prim是加点（最小权边的点）的。

Kruskal Algorithm每次遍历所有边权的值，每次取最小的权边，生成树枝。不一定在算法启动前期边一定连通，可以是孤立存在的非邻接边。已经加入树的边不需要重复遍历。注意图中的边很可能存在相同的权，意味着每次检查最小权边时候，返回的是list。取出最小的权边后，当加入树时候，需要检查是否构成了环，如果构成环，则废弃这个边。

当树的边等于图所有节点数减一时候，算法收敛，结束算法。

import networkx as nx
import matplotlib.pyplot as plt


def my_graph():
    # 构造一个有权边的无向图，然后找出最小生成树
    G = nx.Graph()  # 无向图

    nodes = ['a', 'b', 'c', 'd', 'e', 'f']
    G.add_nodes_from(nodes)

    G.add_edges_from([('a', 'b', {'weight': 6}),
                      ('a', 'c', {'weight': 1}),
                      ('a', 'd', {'weight': 5}),
                      ('b', 'c', {'weight': 5}),
                      ('c', 'd', {'weight': 5}),
                      ('b', 'e', {'weight': 3}),
                      ('c', 'e', {'weight': 6}),
                      ('e', 'f', {'weight': 6}),
                      ('c', 'f', {'weight': 4}),
                      ('d', 'f', {'weight': 2})])

    pos = nx.spring_layout(G)
    nx.draw(G, pos,
            node_color='green',
            node_size=500,
            font_size=10,
            font_color='black',
            edge_color='gray',
            width=1,
            alpha=0.5,
            with_labels=True)

    my_edge_labels = nx.get_edge_attributes(G, 'weight')
    nx.draw_networkx_edge_labels(G, pos, edge_labels=my_edge_labels)

    print('邻接', list(G.adjacency()))

    print('所有边', G.edges())
    g_edges = list(G.edges(data=True))
    print('所有边权', g_edges)

    U = []
    V = g_edges.copy()

    loop_flag = True
    while loop_flag:
        print('----------')
        me = find_min_edge(V.copy())
        for e in me:
            U_temp = U.copy()
            U_temp.append(e)
            G_temp = nx.Graph()
            G_temp.add_edges_from(U_temp)

            try:
                cycle_found = nx.find_cycle(G_temp)
                print('连成环了,放弃这个边', cycle_found)
                cycle = True
            except nx.exception.NetworkXNoCycle:
                print('构图没有形成环')
                cycle = False

            if not cycle:
                U.append(e)
                V.remove(e)

                number_of_edge_temp = G_temp.number_of_edges()
                # 如果形成的图的总边==总节点数-1，说明找到的边已经完全cover
                if (G.number_of_nodes() - 1) == number_of_edge_temp:
                    print('生成最小树，算法结束')
                    loop_flag = False
                    break

        print('U=', U)
        print('V=', V)

    # 把最小生成树的边着色加粗重新描边
    nx.draw_networkx_edges(G, pos,
                           edgelist=U,
                           width=8,
                           alpha=0.5,
                           edge_color="r")

    plt.show()


def find_min_edge(edges):
    min_edge_list = []

    min_edge = min(edges, key=lambda x: x[2]['weight'])
    weight = min_edge[2]['weight']
    min_edge_list.append(min_edge)
    edges.remove(min_edge)

    while True:
        if len(edges) == 0:
            break

        edge = min(edges, key=lambda x: x[2]['weight'])
        w = edge[2]['weight']

        if w == weight:
            min_edge_list.append(edge)

        edges.remove(edge)

    print('找到最小权边', min_edge_list)
    return min_edge_list


if __name__ == '__main__':
    my_graph()

如图：

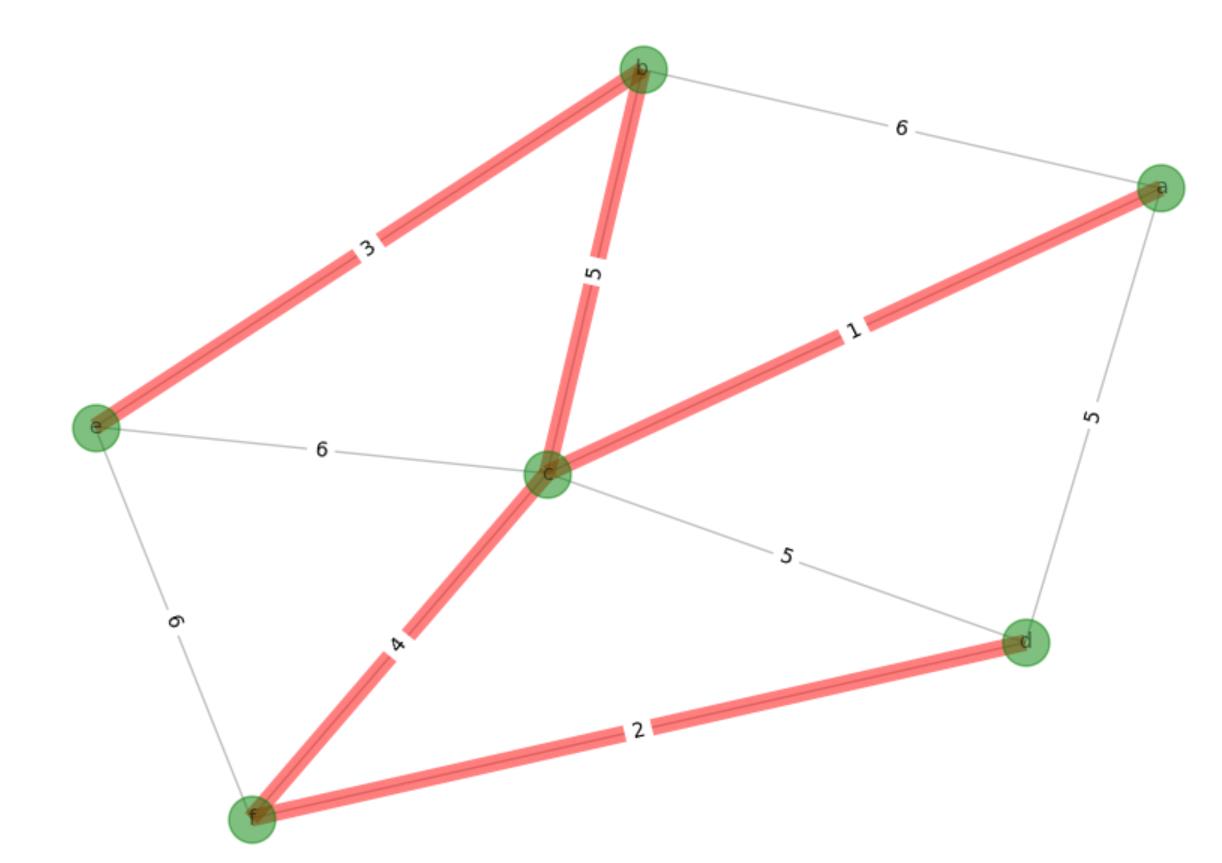
运行日志：

邻接 [('a', {'b': {'weight': 6}, 'c': {'weight': 1}, 'd': {'weight': 5}}), ('b', {'a': {'weight': 6}, 'c': {'weight': 5}, 'e': {'weight': 3}}), ('c', {'a': {'weight': 1}, 'b': {'weight': 5}, 'd': {'weight': 5}, 'e': {'weight': 6}, 'f': {'weight': 4}}), ('d', {'a': {'weight': 5}, 'c': {'weight': 5}, 'f': {'weight': 2}}), ('e', {'b': {'weight': 3}, 'c': {'weight': 6}, 'f': {'weight': 6}}), ('f', {'e': {'weight': 6}, 'c': {'weight': 4}, 'd': {'weight': 2}})]
所有边 [('a', 'b'), ('a', 'c'), ('a', 'd'), ('b', 'c'), ('b', 'e'), ('c', 'd'), ('c', 'e'), ('c', 'f'), ('d', 'f'), ('e', 'f')]
所有边权 [('a', 'b', {'weight': 6}), ('a', 'c', {'weight': 1}), ('a', 'd', {'weight': 5}), ('b', 'c', {'weight': 5}), ('b', 'e', {'weight': 3}), ('c', 'd', {'weight': 5}), ('c', 'e', {'weight': 6}), ('c', 'f', {'weight': 4}), ('d', 'f', {'weight': 2}), ('e', 'f', {'weight': 6})]
----------
找到最小权边 [('a', 'c', {'weight': 1})]
构图没有形成环
U= [('a', 'c', {'weight': 1})]
V= [('a', 'b', {'weight': 6}), ('a', 'd', {'weight': 5}), ('b', 'c', {'weight': 5}), ('b', 'e', {'weight': 3}), ('c', 'd', {'weight': 5}), ('c', 'e', {'weight': 6}), ('c', 'f', {'weight': 4}), ('d', 'f', {'weight': 2}), ('e', 'f', {'weight': 6})]
----------
找到最小权边 [('d', 'f', {'weight': 2})]
构图没有形成环
U= [('a', 'c', {'weight': 1}), ('d', 'f', {'weight': 2})]
V= [('a', 'b', {'weight': 6}), ('a', 'd', {'weight': 5}), ('b', 'c', {'weight': 5}), ('b', 'e', {'weight': 3}), ('c', 'd', {'weight': 5}), ('c', 'e', {'weight': 6}), ('c', 'f', {'weight': 4}), ('e', 'f', {'weight': 6})]
----------
找到最小权边 [('b', 'e', {'weight': 3})]
构图没有形成环
U= [('a', 'c', {'weight': 1}), ('d', 'f', {'weight': 2}), ('b', 'e', {'weight': 3})]
V= [('a', 'b', {'weight': 6}), ('a', 'd', {'weight': 5}), ('b', 'c', {'weight': 5}), ('c', 'd', {'weight': 5}), ('c', 'e', {'weight': 6}), ('c', 'f', {'weight': 4}), ('e', 'f', {'weight': 6})]
----------
找到最小权边 [('c', 'f', {'weight': 4})]
构图没有形成环
U= [('a', 'c', {'weight': 1}), ('d', 'f', {'weight': 2}), ('b', 'e', {'weight': 3}), ('c', 'f', {'weight': 4})]
V= [('a', 'b', {'weight': 6}), ('a', 'd', {'weight': 5}), ('b', 'c', {'weight': 5}), ('c', 'd', {'weight': 5}), ('c', 'e', {'weight': 6}), ('e', 'f', {'weight': 6})]
----------
找到最小权边 [('a', 'd', {'weight': 5}), ('b', 'c', {'weight': 5}), ('c', 'd', {'weight': 5})]
连成环了,放弃这个边 [('a', 'c'), ('c', 'f'), ('f', 'd'), ('d', 'a')]
构图没有形成环
生成最小树，算法结束
U= [('a', 'c', {'weight': 1}), ('d', 'f', {'weight': 2}), ('b', 'e', {'weight': 3}), ('c', 'f', {'weight': 4}), ('b', 'c', {'weight': 5})]
V= [('a', 'b', {'weight': 6}), ('a', 'd', {'weight': 5}), ('c', 'd', {'weight': 5}), ('c', 'e', {'weight': 6}), ('e', 'f', {'weight': 6})]