算法效果评估：均方根误差（RMSE）/ 标准误差

Posted 2021-12-08 bluishglc

评估算法的效果

常见的算法效果评估函数是均方根误差（Root Mean Square Error），在了解这个均方根误差前，需要先熟悉一下其他几个基本方差：

方差（Variance）

方差用于衡量随机变量或一组数据的离散程度。对于方差我们可以用一种朴素的方式理解和记忆：它不是平方的差，而是差的平方求和之后再取平均值，对于计算方差取差的平方这一点，可以很形象地理解为以两点间的直线距离为边得到一个正方型，以面积（平方）的形式度量离散程度，显然面积越大，意味着离散程度越高。

总体方差

总体方差，也叫做有偏估计，其实就是普遍在使用的标准“方差”的概念。计算总体方差需要先计算出总体均值，总体均值的计算方式是：

总体均值：

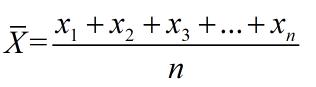
其中，n表示这组数据个数，x1、x2、x3……xn表示这组数据具体数值。然后，基于总体均值，可得：

总体方差：

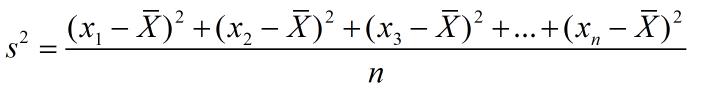
样本方差

但是在实际情况中，总体均值可能无法得到（样本过多或无法穷举），此时往往会通过抽样来获得一个近似值，这个值叫样本方差。

样本方差：

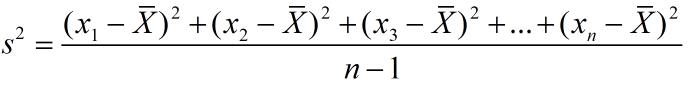
至于样本方差中的分母为什么是n-1，可以这样理解：因为样本方差是用来估计总体中个体之间的变化大小，只拿到一个个体，当然完全看不出变化大小。反之，如果公式的分母不是n-1而是n，计算出的方差就是0——这是不合理的，因为不能只看到一个个体就断定总体的个体之间变化大小为0。

均方差 / 标准差

均方差又常称标准差，是方差的算术平方根，用σ表示。均方差反映的也是一组数据的离散程度。其实方差与标准差反映的都是数据集的离散程度，只是由于方差出现了平方项，导致量纲与原始数据量纲不一致，无法直观反映出偏离程度，所以才有了标准差。

正因为均方差是方差的平方根，所以对应于总体方差和样本方差，就总体均方差（总体标准差）和样本均方差（样本标准差），它们的计算公式分别是：

总体标准差

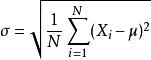
样本标准差

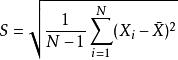
均方误差（mean-square error, MSE）

均方误差MSE通过计算预测值和实际值之间距离（即误差）的平方来衡量模型优劣。即预测值和真实值越接近，两者的均方差就越小。MSE的值越小，说明预测模型描述实验数据具有更好的精确度。均方误差损失又称为二次损失、L2损失，常用于回归预测任务中。如下是均方误差的计算方法：

基于上述表述，均方误差也会这样表述：

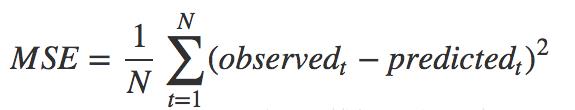
其中observed(t)就是针对数据t的实际输出值（观测到的值），predicted(t)就是对应的预测值。

其实从均方误差MSE的计算公式可以看出，它和方差是高度一致的，只是参与计算的变量(项）不同，所以度量的角度也就不同，方差是用来衡量一组数自身的离散程度，而均方误差是用来衡量观测值（真值）与预测值之间的偏差。

均方根误差（root mean squared error，RMSE）/ 标准误差

均方根误差也称之为标准误差，是均方误差的算术平方根。引入均方根误差与引入标准差（均方查）的原因是完全一致的，即均方误差的量纲与数据量纲不同，不能直观反映离散程度，故在均方误差上开平方根，得到均方根误差：

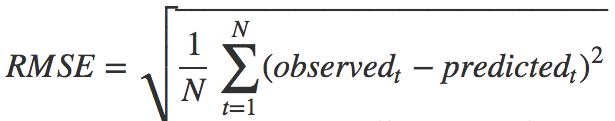
同样的，均方根误差RMSE和标准差的计算公式也是高度近似的：标准差是用来衡量一组数自身的离散程度，而均方根误差是用来衡量观测值（真值）与预测值之间的偏差。

参考文章：

方差、协方差、标准差、均方差、均方根值、均方误差、均方根误差对比分析

均方差损失（Mean Square Error，MSE）