self-attention

Posted 2021-12-08 ^_^|

我们使用self-attention的原因，是考虑在处理Sequence这样的问题时，有没有办法说在考虑整个Sequence的情况下不是说用一个fully-connected这样的方式强硬的处理导致会产生大量参数以及容易overfitting这样的问题

所以有没有更好的方法,来考虑整个Input Sequence的资讯呢,这就要用到我们接下来要跟大家介绍的,Self-Attention这个技术

Self-Attention的运作方式就是，Self-Attention会吃一整个Sequence的资讯

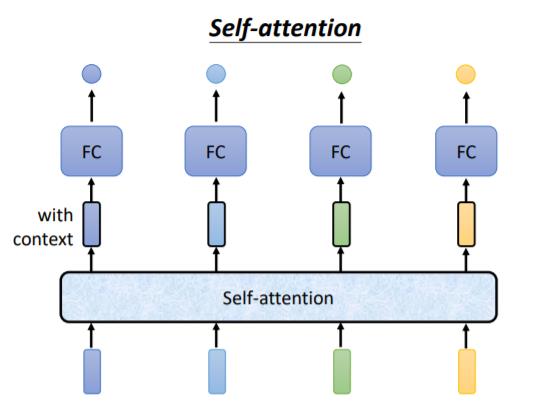
然后你Input几个Vector,它就输出几个Vector,比如说你这边Input一个深蓝色的Vector,这边就给你一个另外一个Vector

这边给个浅蓝色,它就给你另外一个Vector,这边输入4个Vector,它就Output 4个Vector

那这4个Vector有什麼特别的地方呢,这4个Vector,他们都是考虑一整个Sequence以后才得到的,那等一下我会讲说Self-Attention,怎麼考虑一整个Sequence的资讯

Self-Attention不是只能用一次，你可以叠加很多次

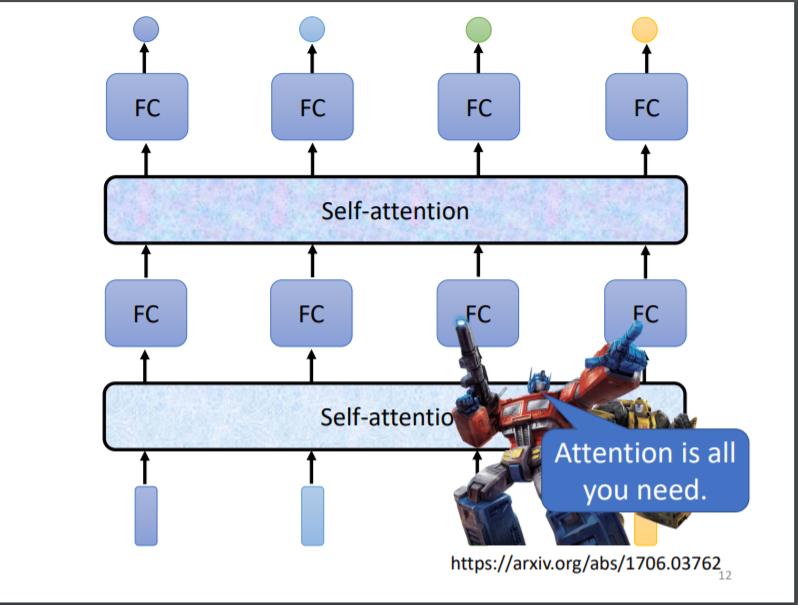
所以可以把Fully-Connected的Network,跟Self-Attention交替使用

• Self-Attention处理整个Sequence的资讯
• Fully-Connected的Network,专注於处理某一个位置的资讯
• 再用Self-Attention,再把整个Sequence资讯再处理一次
• 然后交替使用Self-Attention跟Fully-Connected

Self-Attention过程

Self-Attention的Input,它就是一串的Vector,那这个Vector可能是你整个Network的Input,它也可能是某个Hidden Layer的Output,所以我们这边不是用x来表示它,我们用a来表示它

Self-Attention的output是另外一排b这个向量，那这每一个$b^1$都是考虑了所有的$a^1到a^4$以后才生成出来的,所以这边刻意画了非常非常多的箭头,$b^2,b^3,b^4$同理。

那么接下来就是要具体说明，这个$b^1$究竟是如何产生的

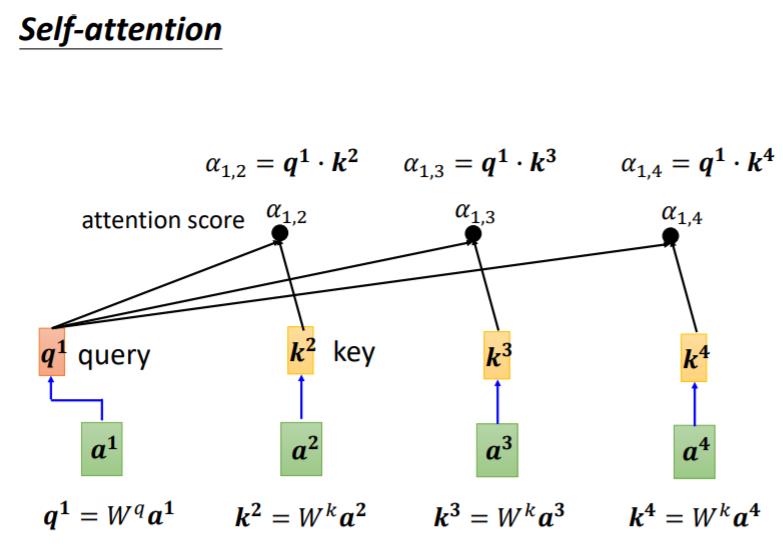
你把$a^1$乘上$W^q$得到$q^1$,那这个q有一个名字,我们叫做Query,它就像是你搜寻引擎的时候,去搜寻相关文章的问题,就像搜寻相关文章的关键字,所以这边叫做Query

然后接下来呢,$a^2,a^3,a^4$你都要去把它乘上$W^k$,得到这个Vector,k这个Vector叫做Key,那你把这个Query q1,跟这个Key k2,算Inner-Product就得到α

我们这边用${\alpha }_{1,2}$来代表说,Query是1提供的,Key是2提供的时候,这个1跟2他们之间的关联性,这个α这个关联性叫做Attention Score,叫做Attention的分数

其实一般在实作的时候，$q^1$也会跟自己算关联性得到${\alpha }_{1,1}$

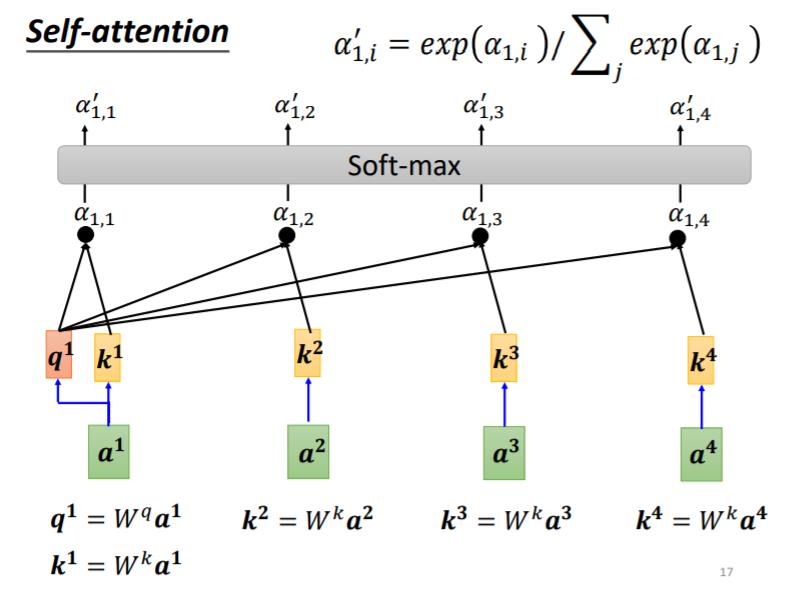
计算出a1跟每个向量的关联性以后，接下来这边会接入一个softmax，得到${\alpha }^{{}^{\prime }}$. 当然其实也不一定要用softmax，也许用ReLU或者可能一些其他的Activation Function甚至能够做得更好

接下来得到这个${\alpha }^{{}^{\prime }}$以后，我们就要根据这个${\alpha }^{{}^{\prime }}$去抽取这个Sequence里面重要的资讯，根据这个$\alpha$我们已经知道说哪些向量跟${\alpha }^1$是最有关系的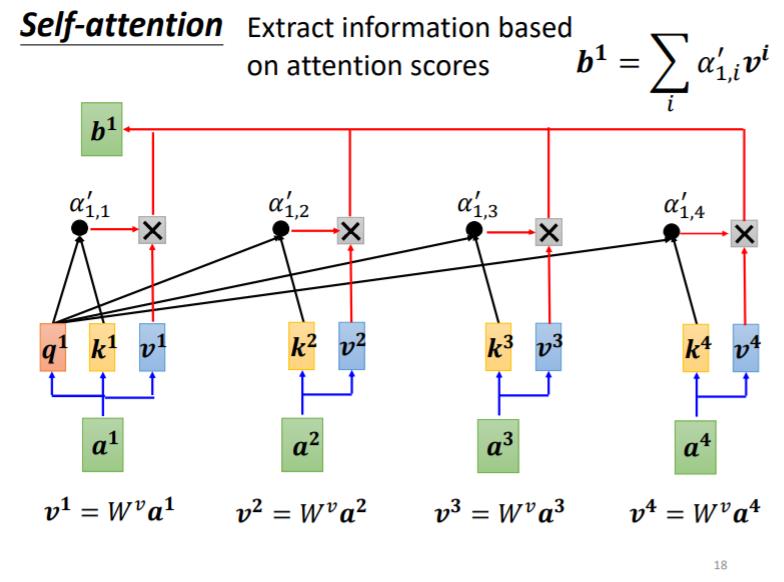
最后得到b的步骤即为

• 首先把$a^1$到$a^4$这边每一个向量，乘上$W^v$得到新的向量，这边分别就是用$v^1{v}^2{v}^3{v}^4$来表示
• 接下来把$v^1$到$v^4$每一个向量都去乘上Attention的分数${\alpha }^{{}^{\prime }}$
• 然后再把它加起来，得到$b^1$
  $$b^1=\sum _i{\alpha }_{1,i}^{{}^{\prime }}{v}^i$$

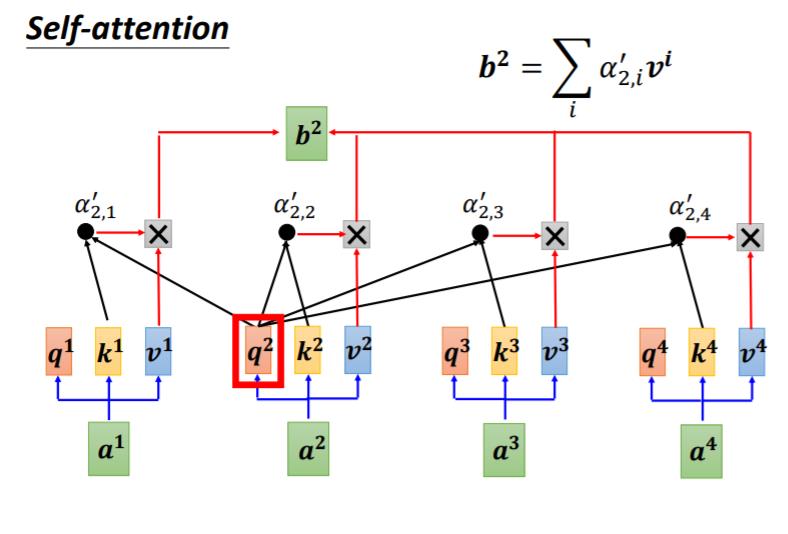
$b^2$的计算过程也就如法$b^1$

那么最终我们得到的一组b的值也就是原先a的值在考虑了整个Sequence之后得到的新的向量

向量化

稍加观察，我们便可以发现我们计算过程中所有的q,k,v,b都是完全可以向量化得到的，在此就不加以赘述

Multi-head Self-attention

Self-attention 有一个进阶的版本,叫做 Multi-head Self-attention, Multi-head Self-attention,其实今天的使用是非常地广泛的

有一些任务,比如说翻译,比如说语音辨识,其实用比较多的 head,你反而可以得到比较好的结果。至於需要用多少的 head,这个又是另外一个 hyperparameter,也是你需要调的

我们在做这个 Self-attention 的时候,我们就是用 q 去找相关的 k,但是相关这件事情有很多种不同的形式,有很多种不同的定义,所以也许我们不能只有一个 q,我们应该要有多个 q,不同的 q 负责不同种类的相关性

所以假设你要做 Multi-head Self-attention 的话,你会怎麼操作呢?

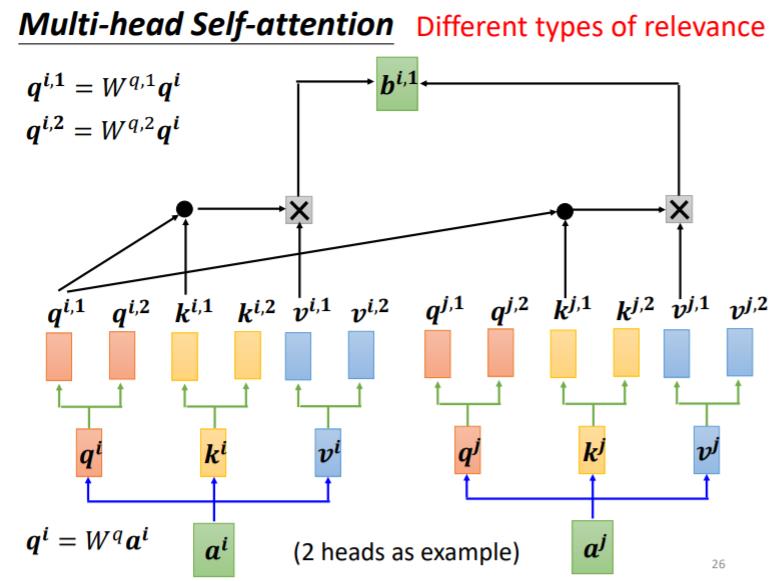
• 先把 $a^i$ 乘上一个矩阵得到 $q^i$
• 再把 $q^i$ 乘上另外两个矩阵，分别得到$q^{i,1}$和$q^{i,2}$

我们认为这个问题，里面有两种不同的相关性，是我们需要产生两种不同的 head，来找两种不同的相关性

剩下的计算如图所示即可，与之前大同小异

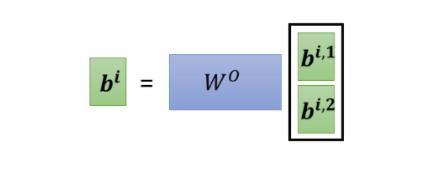
最终我们可能会得到 $b^{i,1},b^{i,2}$这样，然后我们会把他们接起来，然后再乘上一个矩阵，然后得到$b_i$

Positional Encoding

那讲到目前為止,你会发现说 Self-attention 的这个 layer,它少了一个也许很重要的资讯,这个资讯是位置的资讯

对 Self-attention 而言,位置 1 跟位置 2 跟位置 3 跟位置 4,完全没有任何差别,这四个位置的操作其实是一模一样,对它来说 q1 到跟 q4 的距离,并没有特别远,1 跟 4 的距离并没有特别远,2 跟 3 的距离也没有特别近

Each position has a unique positional vector $e^i$

你做 Self-attention 的时候,如果你觉得位置的资讯是一个重要的事情,那你可以把位置的资讯把它塞进去,怎麼把位置的资讯塞进去呢,这边就要用到一个叫做 positional encoding 的技术

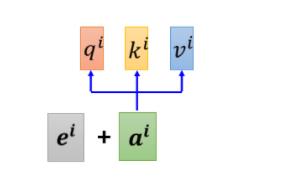
你为每一个位置设定一个vector叫做positional vector，这边用$e^i$来表示，上标 i 代表是位置，每一个不同的位置就有不同的vector，然后将这个$e^i$加到$a^i$上面，就结束了

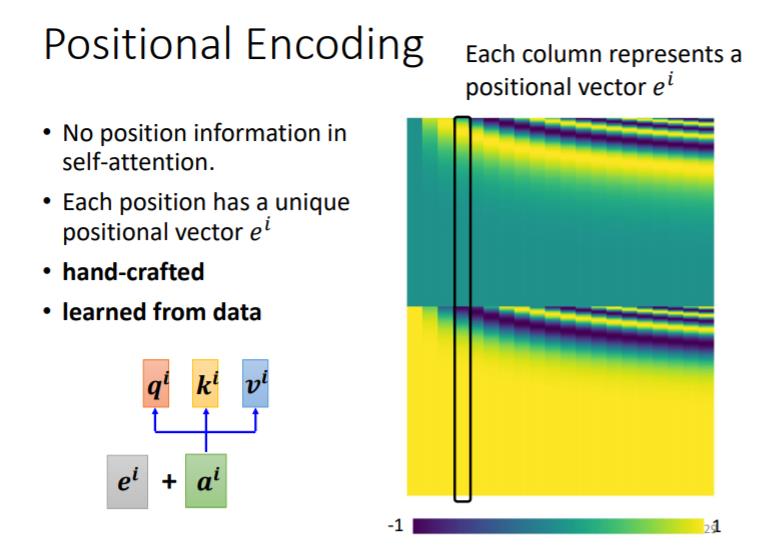
最早的 transformer, 就 Attention Is All You Need 那篇 paper 里面，它的$e^i$如上

关于 positional encoding 仍然是一个尚待研究的问题，下面也是有人做的一些相关研究

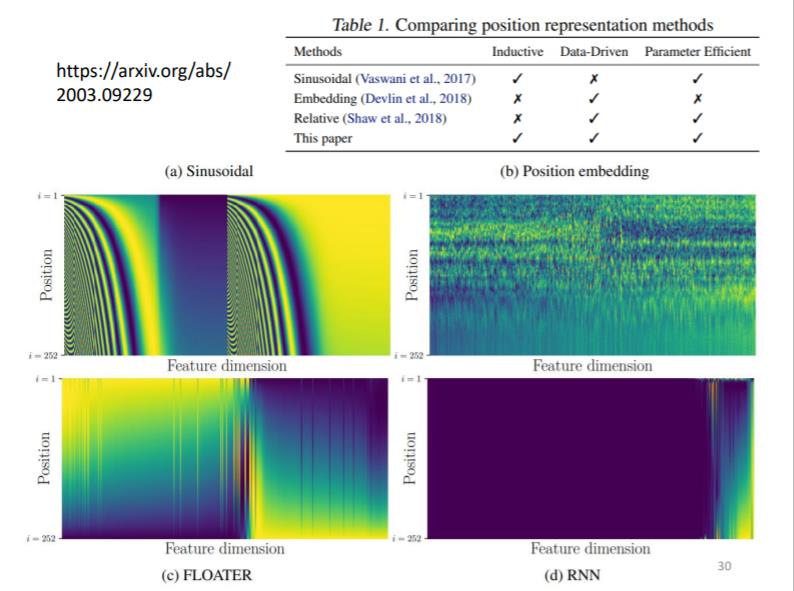
Applications …

Self-attention 当然是用的很广，我们已经提到很多次 transformer 这个东西

那我们大家也都知道说,在 NLP 的领域有一个东西叫做 BERT,BERT 裡面也用到 Self-attention,所以 Self-attention 在 NLP 上面的应用,是大家都耳熟能详的

Self-attention for image

那其实 Self-attention ,还可以被用在影像上

一张图片啊,我们把它看作是一个很长的向量,那其实一张图片,我们也可以换一个观点,把它看作是一个 vector 的 set

你可以把每一个位置的 pixel,看作是一个三维的向量,所以每一个 pixel,其实就是一个三维的向量,那整张图片,其实就是 5 乘以 10 个向量的set

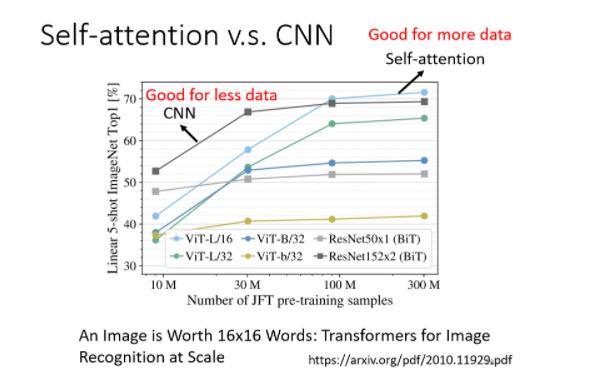
Self-attention v.s. CNN

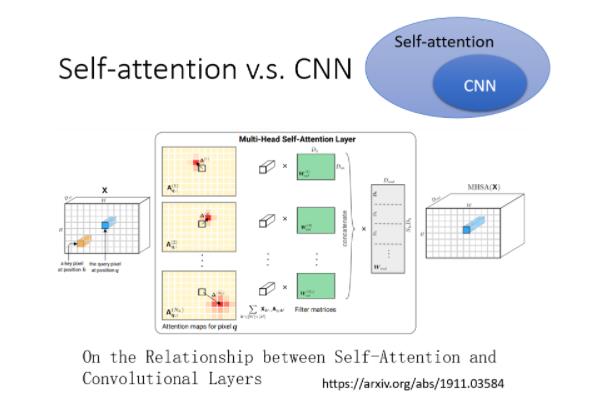
在这篇 paper 裡面,会用数学的方式严谨的告诉你说,其实这个 CNN就是 Self-attention 的特例,Self-attention 只要设定合适的参数,它可以做到跟 CNN 一模一样的事情

Self-attention v.s. RNN

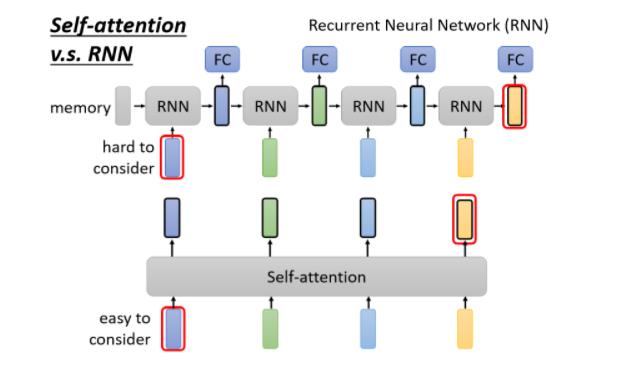
当然一个非常显而易见的不同,你可能会说,这边的每一个 vector,它都考虑了整个 input 的 sequence,而 RNN 每一个 vector,只考虑了左边已经输入的 vector,它没有考虑右边的 vector,那这是一个很好的观察

但是 RNN 其实也可以是双向的,所以如果你 RNN 用双向的 RNN 的话,其实这边的每一个 hidden 的 output,每一个 memory 的 output,其实也可以看作是考虑了整个 input 的 sequence

但是假设我们把 RNN 的 output,跟 Self-attention 的 output 拿来做对比的话,就算你用 bidirectional 的 RNN,还是有一些差别的

• 对 RNN 来说,假设最右边这个黄色的 vector,要考虑最左边的这个输入,那它必须要把最左边的输入存在 memory 裡面,然后接下来都不能够忘掉,一路带到最右边,才能够在最后一个时间点被考虑
• 但对 Self-attention 来说没有这个问题,它只要这边输出一个 query,这边输出一个 key,只要它们 match 得起来,天涯若比邻,你可以从非常远的 vector,在整个 sequence 上非常远的 vector,轻易地抽取资讯,所以这是 RNN 跟 Self-attention,一个不一样的地方

还有另外一个更主要的不同是,RNN 今天在处理的时候, input 一排 sequence,output 一排 sequence 的时候,RNN 是没有办法平行化的