数据结构—树

Posted 2021-12-08 之墨_

树、查找算法

• 树的定义
• • 树的性质
  • 树的存储结构
  • • 双亲存储结构
    • 孩子链存储结构
    • 孩子兄弟链存储结构
  • 二叉树的定义
  • • 满二叉树
    • 完全二叉树
  • 二叉树的性质
  • 二叉树的存储结构
  • • 顺序存储
    • 链式存储
    • 创建二叉树
• 查找
• • 二分查找
  • • 代码实现

树的定义

树(tree)是由 n(n≥0)个结点(或元素)组成的有限集合(记为 T)。
如果x=0,它是一棵空树,这是树的特例
如果n>0,这n个结点中有且仅有一个结点作为树的根结点,简称为根(root),其余结点可分为 m(m≥0)个互不相交的有限集 Ti,Tz,…,T,,其中每个子集本身又是一棵符合本定义的树,称为根结点的子树(subtree)

树的性质

1. 树中的结点数等于所有结点的度数之和+1
2. 度为m的树中第i层上最多有m的i-1次方个结点
3. 高度为h的m次树最多有（（m的h次方）-1）/（m-1）
4. 具有n个结点的m次树的最小高度为logm(n(m-1)+1)

树的存储结构

双亲存储结构

typedef struct{
int data ///存放结点的值
int parent; ///存放双亲的位置
}PTree[MaxSize];///PTree为双亲存储结构类型

孩子链存储结构

typedef struct node{
int data;///结点的值
struct node *sons[MaxSons];///指向孩子结点
}TSonNode;///孩子链存储结构中的结点类型

孩子兄弟链存储结构

typedef struct tnode{
int data;///结点的值
struct tnode *hp;///指向兄弟
struct tnode *vp;///指向孩子结点
}TSBNode;///孩子兄弟链存储结构中的结点类型

二叉树的定义

二叉树(binary tree)是一个有限的结点集合,这个集合或者为空,或者由一个根结点和两棵互不相交的称为左子树(left subtree)和右子树(right subtree)的二叉树组成

二叉树的结构简单,存储效率高,其运算算法也相对简单,而且任何 m次树都可以转化为二叉树结构,因此二叉树具有很重要的地位

二叉树和度为 2 的树(2 次树)是不同的,对于非空树,其差别表现在以下两点:

• 度为 2 的树中至少有一个结点的度为 2,而二叉树没有这种要求;
• 度为 2 的树不区分左、右子树,而二叉树是严格区分左、右子树的。

满二叉树

一棵二叉树中，如果所有分支结点都有左孩子结点和右孩子结点，并且叶子结点都集中在二叉树的最下一层，这样的二叉树称为满二叉树
非空满二叉树的特点：

• 叶子结点都在最下一层
• 只有度为0和度为2的结点
  

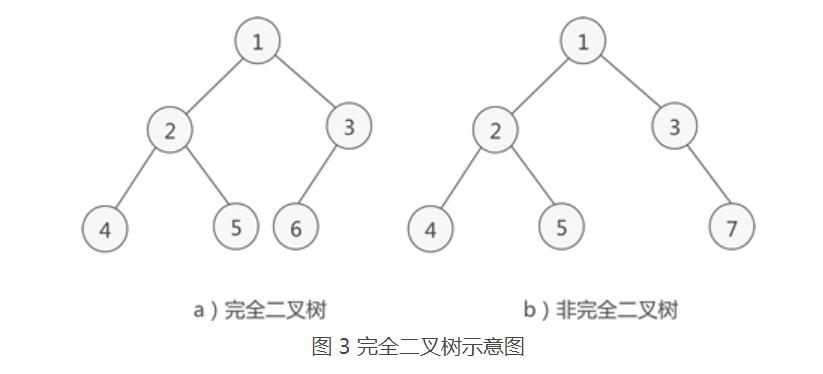
完全二叉树

若二叉树中最多只有最下面两层的结点的度数可以小于2，并且最下面一层的叶子结点都依次排列在该层最左边的位置上，则这样的二叉树称为完全二叉树
非空完全二叉树的特点：

• 叶子结点只可能在最下面两层出现
• 对于最大层次中的叶子结点，都依次排列在该层最左边的位置上
• 如果有度为1的结点，只可能有1个，且该结点只有左孩子而无右孩子
• 按层次编号时，一旦出现编号为i的结点是叶子结点或只有左孩子，则编号大于i的结点均为叶子结点
• 当结点总数n为奇数时，n1 = 0 ，当结点总数n为偶数时，n1 = 1
  完全二叉树最重要的性质：
  如果n个节点的完全二叉树的节点按照层次并按从左到右的顺序从0开始编号，对于每个结点都有：

1. 序号为0的节点是根对于i>0，其父节点的编号为(i-1)/2
2. 若2·i+1<n，其左子节点的序号为2·i+1，否则没有左子节点
3. 若2·i+2<n，其右子节点的序号为2·i+2，否则没有右子节点

对于一个树高为h的二叉树，如果其第0层至第h-1层的节点都满。如果最下面一层节点不满，则所有的节点在左边的连续排列，空位都在右边。这样的二叉树就是一棵完全二叉树

二叉树的性质

1. 非空二叉树上的叶子结点数等于双分支结点数+1
2. 非空二叉树的第i层上最多有 2的(i-1)次方个结点（i≥1）
3. 高度为h的二叉树最多有2的h次方-1个结点（h≥1）

二叉树的存储结构

顺序存储

顺序存储结构类型声明

typedef int SqBinTree[MaxSize];

链式存储

/**二叉链结点类型*/
typedef struct node{
int data;       ///数据元素
struct node *lchild;///指向左孩子结点
struct node *rchild;///指向右孩子结点
}BTNode;

创建二叉树

/**创建二叉树*/
void CreatBTree(BTNode *&b,char *str){
BTNode *St[MaxSize],*p;///St数组作为顺序栈
int top = -1,k,j=0;
char ch;
b = NULL;
ch = str[j];
while(ch != '\\0'){
    switch(ch){
    case '(' :top++;St[top] = p;k=1;break;///处理左孩子结点
    case ')' :top--;break;///栈顶结点的子树处理完毕
    case ',' :k=2;break;///开始处理右孩子结点
    default:p=(BTNode *)malloc(sizeof(BTNode));///创建一个结点p
            p->data = ch;///存放节点值
            p->lchild = p->rchild = NULL;///左右指针设置为空
            if(b == NULL)///若尚未建立根节点
                b = p;///p所结点就作为根节点
            else{
                switch(k){
                case 1:St[top]->lchild = p;break;///新建结点作为栈顶结点的左孩子
                case 2:St[top]->rchild = p;break;///新建结点作为栈顶结点的右孩子
                }
            }
    }
    j++;///继续扫描str
    ch = str[j];
}
}

查找

_{用于查找的运算的顺序表采用数组表示，数组元素类型声明如下}

typedef struct{
int key;
int data;
}RecType;

二分查找

折半查找(binary search) 又称 二分查找,它是一种效率较高的查找方法。但是,折半查找要求线性表是有序表,即表中的元素按关键字有序。在下面的讨论中,假设有序表是递增有序的
折半查找的基本思路是设 R[low..high]是当前的查找区间,首先确定该区间的中点位置 mid=L(low+high)/2」,然后将待查的k值与R[mid].key 比较：

1. 若k=R[mid].key,则查找成功并返回该元素的逻辑序号
2. 若k<R[mid].key,则由表的有序性可知 R[mid..high].key 均大于k,因此若表中存在关键字等于k的元素,则该元素必定是在位置 mid 左边的子表 R[low..mid-1]中,故新的查找区间是左子表 R[low..mid-1]
3. 若k>R[mid]. key,则关键字为k 的元素必在 mid 的右子表 R[mid+1..high]中，即新的查找区间是右子表 R[mid+1..high]。下一次查找是针对新的查找区间进行的

查找区间的中点位置上的关键字比较,就可确定查找是否成功,不成功则当前的查找区间缩小一半。重复这一过程直到找到关键字为k的元素,或者直到当前的查找区间为空(即查找失败)时为止

代码实现

/**二分查找*/
BinSearch(RecType R[], int len,int k){
int low = 0,high = len-1,mid;
while(low <= high){     ///当前区间存在元素时执行循环
    mid = (low + high)/2;
    if(k == R.[mid].key) ///查找成功返回其逻辑序号+1
    return mid+1;
    if(k < R.[mid].key) ///所要查找的值比中间值小
    high = mid-1;       ///在中间值的左区间继续查找
    else                ///所要查找的值比中间值大
    low =  mid+1;       ///在中间值的右区间继续查找
}
return 0;               ///查询失败返回0
}