树的应用——并查集及实现代码

Posted 2021-12-08 薛定谔的猫ovo

文章目录

• • 什么是并查集
  • • 亲戚问题
  • 并查集的实现
  • • 改进——路径压缩
    • 进一步改进——合并
  • 并查集的用途

---

什么是并查集

 并查集是一种树型的数据结构，用于处理一些不相交集合（disjoint sets）的合并及查询问题。常常在使用中以森林来表示。

 并查集支持以下3种操作：

• 初始化（Initial）：将集合中的每个元素初始化为只有一个单元素的子集合。
• 合并（Union）：把两个不相交的集合合并为一个集合。
• 查询（Find）：查询两个元素是否在同一个集合中。

这样来说还是有点抽象，所以先来看看并查集最直接的一个应用场景：亲戚问题。

---

亲戚问题

问题描述
若某个家族人员过于庞大，要判断两个人是否是亲戚。现在给出某个亲戚关系图，求任意给出的两个人是否有亲戚关系。

输入
第一行：三个整数n,m,p，（n<=5000,m<=5000,p<=5000），分别表示有n个人，m个亲戚关系，询问p对亲戚关系。
以下m行：每行两个数Mi，Mj，1<=Mi，Mj<=N，表示Mi和Mj具有亲戚关系。
接下来p行：每行两个数Pi，Pj，询问Pi和Pj是否具有亲戚关系。

输出
共p行，每行一个’Yes’或’No’。表示第pi个询问的答案为“有”或“没有”亲戚关系。

那么如何实现这个问题呢？
其实很简单，首先把所有人划分到若干个不相交的集合中，每个集合里的人彼此是亲戚。那么判断两个人是否为亲戚时，只需要看它们是否属于同一个集合即可。
因此，这时就可以考虑用并查集来实现这个问题。

---

为了方便理解，现在我们给出具体的家族人员及其亲戚关系：
假设共有7个人，分别编号为{1，2，3，4，5，6，7}；亲戚关系为：{1，2}，{2，4}，{3，5}，{5，6}，{4，7}。
问1和7是否有亲戚关系、2和6是否有亲戚关系？

运用并查集的思想，建立集合。
<1>初始化时，每个元素（人）自成一个单元素子集合。

<2>现在我们知道1和2是亲戚，于是便把2合并到1的集合中。

<3>2和4是亲戚，那么再将4合并到2的集合中，注意此时2和1已经在一个集合中了。

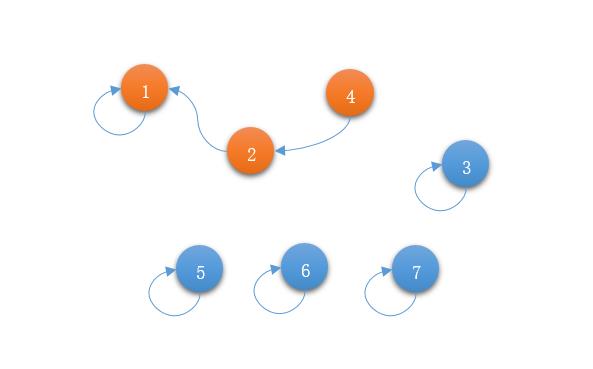
<4>继续，3和5是亲戚，将5合并到3的集合中。

<5>5和6是亲戚，将6合并到5的集合中。

<6>最后，4和7是亲戚，将7合并到4的集合中。

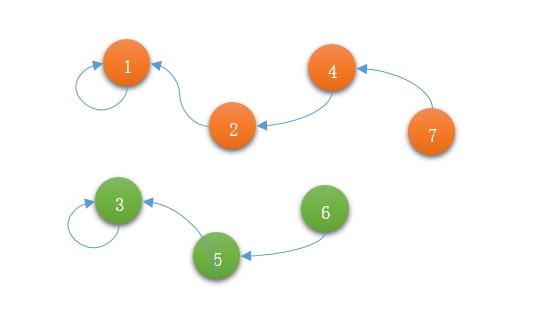
至此，全部合并完成。
由于1和7在同一个集合中，故1和7有亲戚关系。而2和6不在同一个集合中，故2和6没有亲戚关系。

---

并查集的实现

根据上个亲戚问题的实例，我们可以写出并查集的代码。

1、初始化Init

const int MAX = 100;
int father[MAX];
//初始化
void Init(int n){
    for(int i=0; i<n; i++){
        father[i] = i; //每个结点的父结点为自身
    }
}

2、查找Find

//查找
int Find(int x){
    if(father[x] == x)
        return x;
    else
        return Find(father[x]);
}

一层一层向上访问父结点，直至根结点（父结点是本身的结点）。
判断两个元素是否属于同一个集合，只需要看它们的根结点是否相同即可。

3、合并Union

//合并
void Union(int x, int y){
    father[Find(x)] = Find(y);
}

先找到这两个结合的代表元素，然后将前者的父结点设为后者的即可，或者相反也可以。

---

改进——路径压缩

简单的并查集效率是比较低的。看下面这个例子：
如下图所示，将4合并到2所在的集合中，Union(2,4)

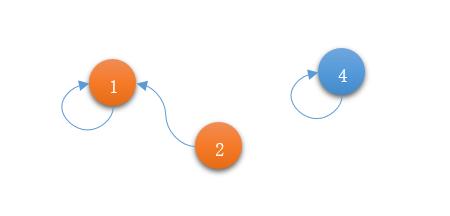
首先，由2找到1，即Find (2)=1，father[1] = 4，于是变成了这样：

接着，又找到了7，假设需要执行Union(2,7) ：
从2找到1，再找到4，然后father[4] = 7，于是变成了这样：

这样会形成一条长长的链，随着链越来越长，要想从底部找到根结点就越来越难。

解决方案：路径压缩。我们只关系一个元素对应的根结点，那么每个元素到根结点的路径尽可能短，最好只有一段：

要想实现这个功能，只需要在查询的过程中，将沿途中每个结点的父结点都设置为根结点即可。代码如下：

2、查找Find

//查找
int Find(int x){
    if(x != father[x]){
        father[x] = Find(father[x]);  //父结点设为根结点
    }
    return father[x];
}

---

进一步改进——合并

很多人有这样一个误解，认为路径压缩优化之后，并查集始终都是一个菊花图（即只有两层的树的俗称）。但其实，由于路径压缩只在查询时进行，也只压缩一条路径，所以最终并查集的结构仍然是比较复杂的。
例如，要合并7和8 ，如果可以选择的话，是将7设为8的父结点还是将8设为7的父结点呢？

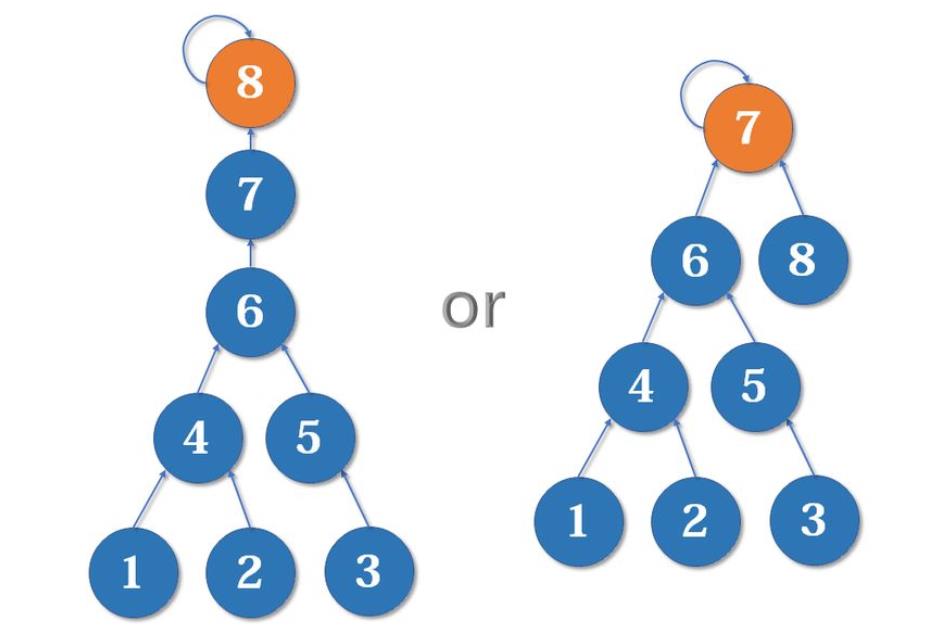
显然应该是将8的父结点设为7，因为如果把7的父结点设为8，会使树的深度加深，原来树中每个元素到根结点的距离都变长了，之后寻找根结点的路径也会变长。

所以，我们应该把较矮的树往较高的树上合并。

为此，引入一个height数组，记录每个结点的高度。

1、初始化Init

const int MAX = 100;
int father[MAX];
int height[MAX];
//初始化
void Init(int n){
    for(int i=0; i<n; i++){
        father[i] = i; //每个结点的父结点为自身
        height[i] = 0; //每个结点的高度为0
    }
}

2、查找Find

//查找
int Find(int x){
    if(x != father[x]){
        father[x] = Find(father[x]);
    }
    return father[x];
}

3、合并Union

//合并
void Union(int x, int y){
    x = Find(x);
    y = Find(y);
    if(x != y){ //矮树作为高数的子树
        if(height[x] < height[y]){
            father[x] = y;
        }else if(height[x] > height[y]){
            father[y] = x;
        }else{
            father[y] = x;
            height[x]++;
        }
    }
}

---

并查集的用途

并查集一般用在以下几个方面：
1、判断无向图的连通性。若连通分支数等于1，则连通。
2、判断增加一条边是否会产生环，用在求解最小生成树的Kruskal算法里。