图的基本概念

Posted 2021-12-08 薛定谔的猫ovo

文章目录

• • 图的定义
  • 图的一些基本概念
  • • 有向图
    • 无向图
    • 简单图
    • 多重图
    • 完全图（也称简单完全图）
    • • 无向完全图
      • 有向完全图
    • 子图
    • 连通、连通图和连通分量
    • • 连通
      • 连通图
      • 连通分量
    • 强连通、强连通图、强连通分量
    • • 强连通
      • 强连通图
      • 强连通分量
    • 生成树、生成森林
    • • 生成树
      • 生成森林
    • 顶点的度、入度和出度
    • • 无向图的度
      • 有向图的出度、入度
    • 边的权和网
    • 路径、路径长度
    • 简单路径、简单回路
    • 距离

–

图的定义

 图G是由顶点集V和边集E组成，记为G=(V,E)，其中V(G)表示图G中的顶点的有穷非空集合，|V|表示顶点个数，E(G)表示边的有穷集合，|E|表示边的个数。

 注意，线性表可以是空表，树也可以是空树，但图不可以是空图。也就是说，图中不能一个顶点也没有，图的顶点集V一定非空，但是边集V可以为空，此时图中只有顶点而没有边。

---

图的一些基本概念

有向图

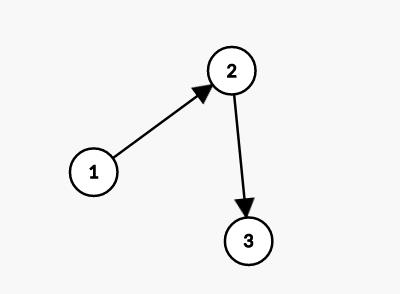
若E是有向边（也称弧）的有限集合时，则图G为有向图。

弧是顶点的有序对，记为<v,w>，其中v、w是顶点，v称为弧尾，w称为弧头，<v,w>称为从顶点v到顶点w的弧，也称为v邻接到w，或w邻接自v。

---

无向图

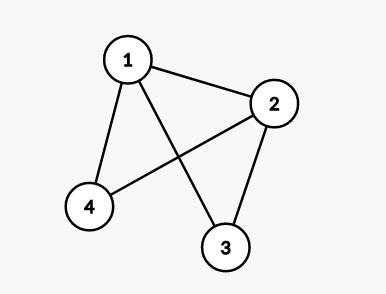
若E是无向边（简称边）的有限集合时，则图G为无向图。

边是顶点的无序对，记为(v,w)或(w,v)，因为(v,w)=(w,v)，其中v、w是顶点。
可以说顶点v和顶点w互为邻接点。边(v,w)依附于顶点v和w，或者说边(v,w)和顶点v、w相关联。

---

简单图

一个图G若满足：
①不存在重复边；②不存在顶点到自身的边；则称图G为简单图。
一般数据结构课程中中只讨论简单图。

多重图

若图G中某两个结点之间的边数多于一条，又允许顶点通过一条边和自己关联，则G为多重图。多重图和简单图的定义是相对的。

---

完全图（也称简单完全图）

无向完全图

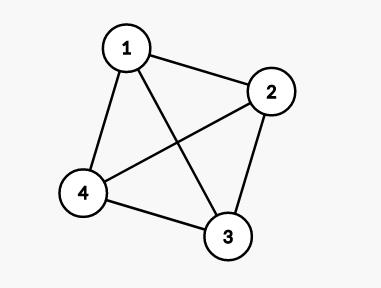
在无向图中，若任意两个顶点之间都存在边，则称该图为无向完全图。
含有n个顶点的无向完全图有n(n-1)/2条边。如下图所示：

有向完全图

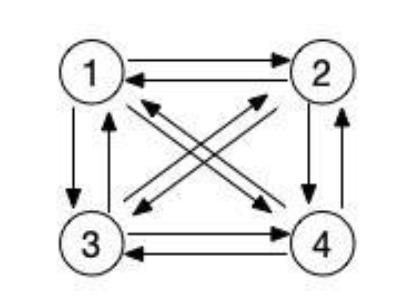
在有向图中，若任意两个顶点之间都存在方向相反的两条弧，则称该图为有向完全图。
含有n个顶点的有向完全图有n(n-1)条有向边。如下图所示：

---

子图

设有两个图G=(V,E)和G’=(V’,E’)，若V’是V的子集，且E’是E的子集，则称G’是G的子图。
若有满足V=V’的图G’，则称G’为G的生成子图。

---

连通、连通图和连通分量

连通

在无向图中，若从顶点v到顶点w有路径存在，则称v和w是连通的。

连通图

若图G中任意两个顶点都是连通的，则称图G为连通图，否则称为非连通图。
若一个图有n个顶点，并且边数小于n-1，则此图必是非连通图。

连通分量

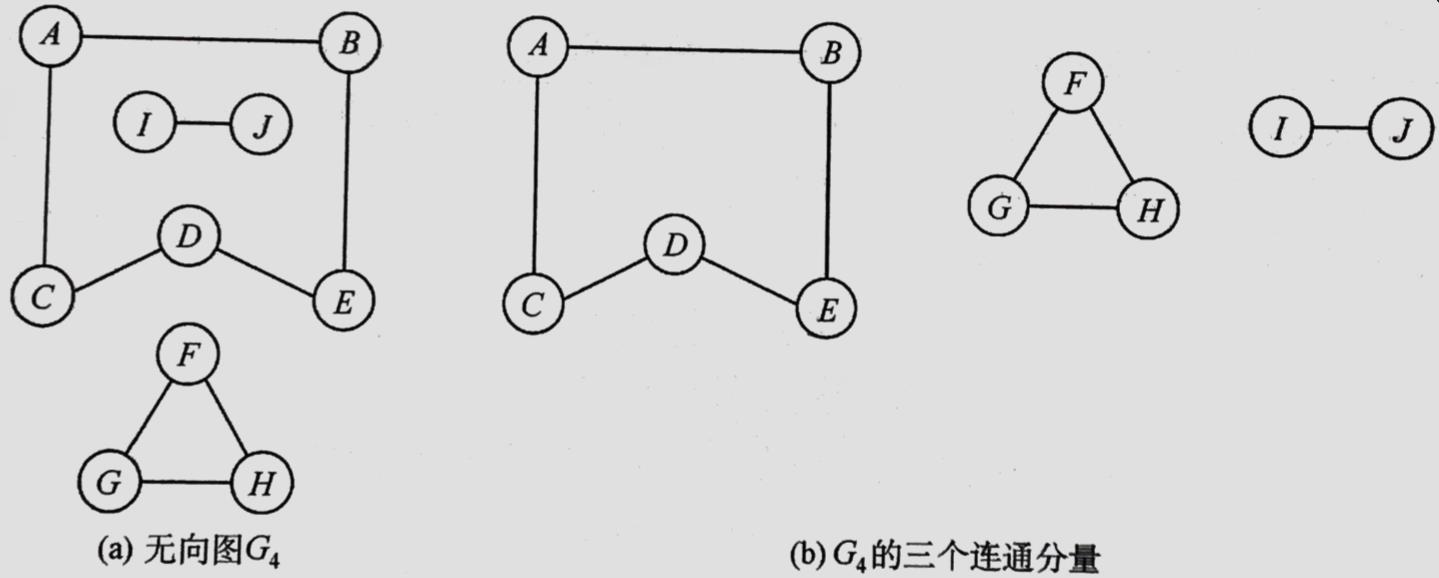
无向图中的极大连通子图称为连通分量。
极大连通子图即要求该连通子图包含其所有的边。
极小连通子图是既要保持图连通又要使得边数最少的子图。

---

强连通、强连通图、强连通分量

强连通

在有向图中，若从顶点v到顶点w和从顶点w到顶点v之间都有路径，则称这两个顶点是强连通的。

强连通图

若图中任何一对顶点都是强连通的，则称此图为强连通图。

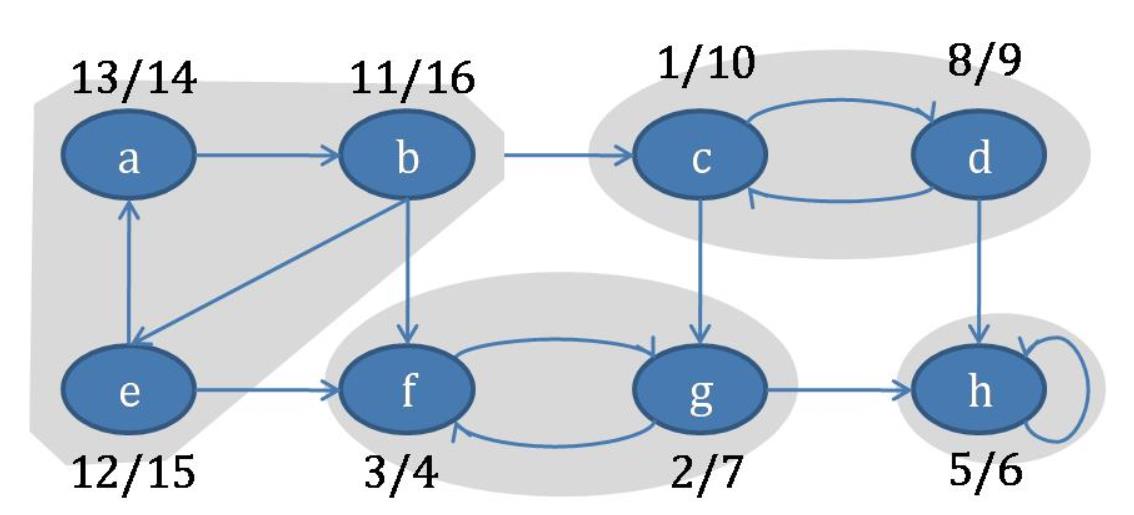
强连通分量

有向图中，极大强连通子图称为有向图的强连通分量。
注意：强连通图、强连通分量只是针对有向图而言的。一般在无向图中讨论连通性，在有向图中考虑强连通性。

---

生成树、生成森林

生成树

连通图的生成树是包含图中全部顶点的一个极小连通子图。
若图中顶点数为n，则它的生成树含有n-1条边。如下图所示：

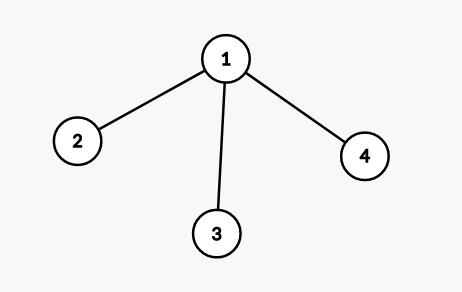
对于生成树而言，如果删去它的一条边，就会变成非连通图；若加上一条边则会形成一个回路。

生成森林

在非连通图中，连通分量的生成树构成了非连通图的生成森林。

---

顶点的度、入度和出度

图中每个顶点的度定义为以该顶点为一个端点的边的数目，$d_i$表示顶点$i$的度。

无向图的度

对于无向图，顶点的度是指依附于该顶点的边的条数。
在具有n个顶点、e条边的无向图中，所有顶点的度数之和等于边数的两倍，即$$\sum _{i=1}^n{d}_i=2e$$
因为每条边和两个顶点相关联。

有向图的出度、入度

对于有向图，顶点v的度分为入度和出度：
入度是以顶点$v_i$为终点的有向边的数目，记为$d_i^{in}$ ；出度是以顶点$v_i$为起点的有向边的数目，记为$d_i^{out}$ 。

顶点v的度 = v的入度 +v的出度，即$d_v$ = $d_i^{in}$ + $d_i^{out}$ .

在具有n个顶点、e条边的有向图中，${\sum }_{i=1}^n{d}_i^{in}$ = ${\sum }_{i=1}^n{d}_i^{out}$ = e，即有向图的全部顶点的入度之和与出度之和相等，都等于边数。
这是因为每条有向边都有一个起点和终点。

---

边的权和网

在一个图中，每条边上都可以表上具有某种含义的数值，该数值称为该边的权值。
这种边上带有权值的图称为带权图，也称网。

---

路径、路径长度

顶点$v_p$到顶点$v_q$之间的一条路径是指顶点序列$v_p$，$v_{i_1}$，$v_{i_2}$，……，$v_{i_m}$，$v_q$。
路径上边的数目称为路径长度。

---

简单路径、简单回路

在路径序列中，顶点不重复出现的路径称为简单路径。
除第一个顶点和最后一个顶点外，其余顶点不重复出现的回路称为简单回路。

---

距离

从顶点u出发到顶点v的最短路径若存在，则此路径的长度称为从u到v的距离。
若从u到v根本不存在路径，则记该距离为无穷（$\infty$）。