从Matlab平台进行FFT到ARM平台C语言FFT频谱分析
Posted “逛丢一只鞋”
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了从Matlab平台进行FFT到ARM平台C语言FFT频谱分析相关的知识,希望对你有一定的参考价值。
Matlab FFT 时域、频域分析
FFT是离散傅立叶变换的快速算法,可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。这就是很多信号分析采用FFT变换的原因。另外,FFT可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。
虽然很多人都知道FFT是什么,可以用来做什么,怎么去做,但是却不知道FFT之后的结果是什意思、如何决定要使用多少点来做FFT。
现在就根据实际经验来说说FFT结果的具体物理意义。一个模拟信号,经过ADC采样之后,就变成了数字信号。采样定理告诉我们,采样频率要大于信号频率的两倍,这些我就不在此罗嗦了。
采样得到的数字信号,就可以做FFT变换了。N个采样点,经过FFT之后,就可以得到N个点的FFT结果。为了方便进行FFT运算,通常N取2的整数次方。
信号频率分析
假设采样频率为Fs,信号频率f,采样点数(序列长度)为N。那么FFT之后结果就是一个为N点的复数。每一个点就对应着一个频率点。 这个点的模值,就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢?
% 生成一个自定义正弦波+噪声信号,然后进行FFT运算
clc;close all;clear all;
Fs=8192; %采样频率
T=1/Fs;
N=8192; %序列长度
f1=400;
f2=1200;
f3=2400;
t=(0:1:N-1)*T;
y=1+2*sin(2*pi*f1*t)+3*sin(2*pi*f2*t+pi/2)+5*sin(2*pi*f3*t+pi/4); %生成输入信号
figure(1)
plot(t, y);
% filename = 'sine.wav';
% audiowrite(filename,y,Fs);
Y = fft(y, N); %作FFT变换
A = abs(Y); %计算幅值
figure(2)
plot(0:1:(N-1), A);title('Matlab N=1024');xlabel('N');ylabel('Amplitude');%作图
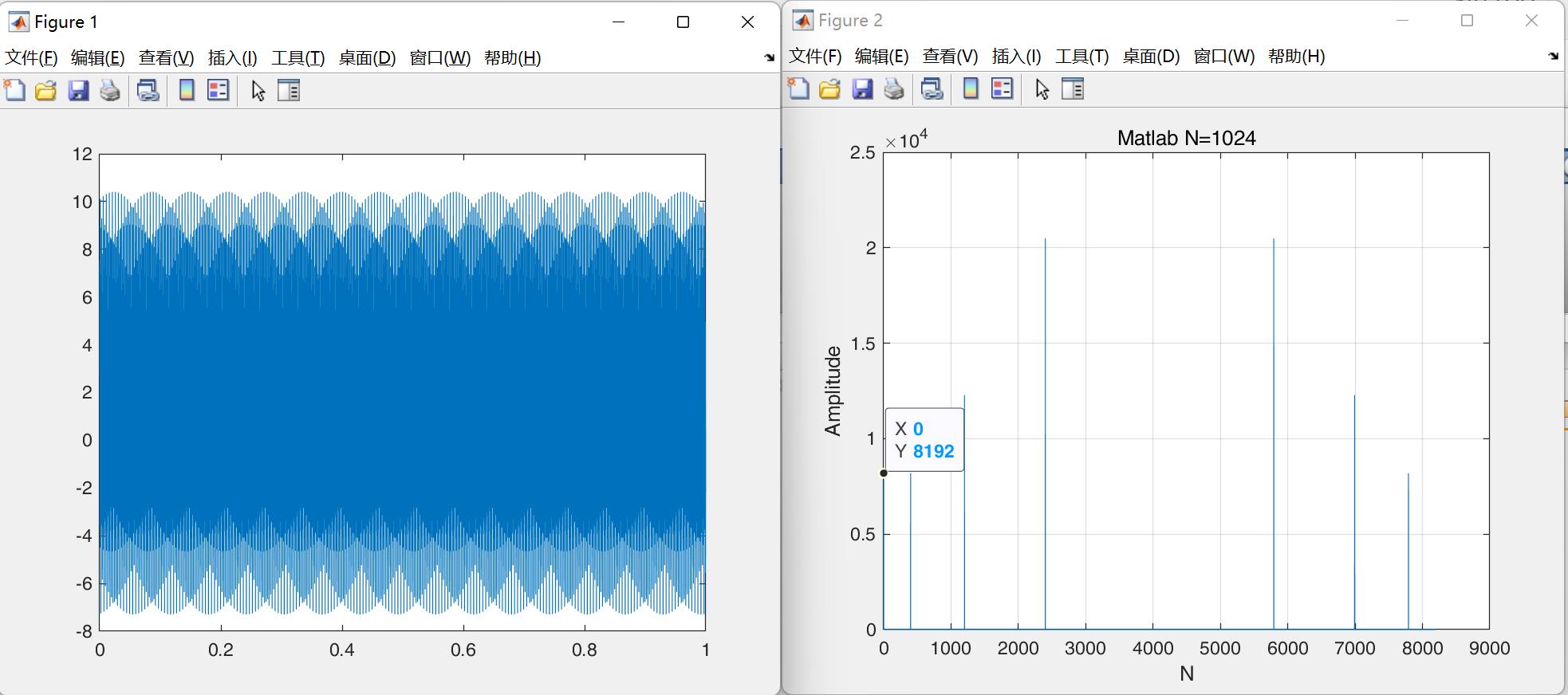
假设原始信号的峰值为A,那么FFT的结果的每个点(除了第一个点直流分量之外)的模值就是A的N/2倍。而第一个点就是直流分量,它的模值就是直流分量的N倍。由图可看出频谱图中第一个点的幅值为直流分量1的8192倍。
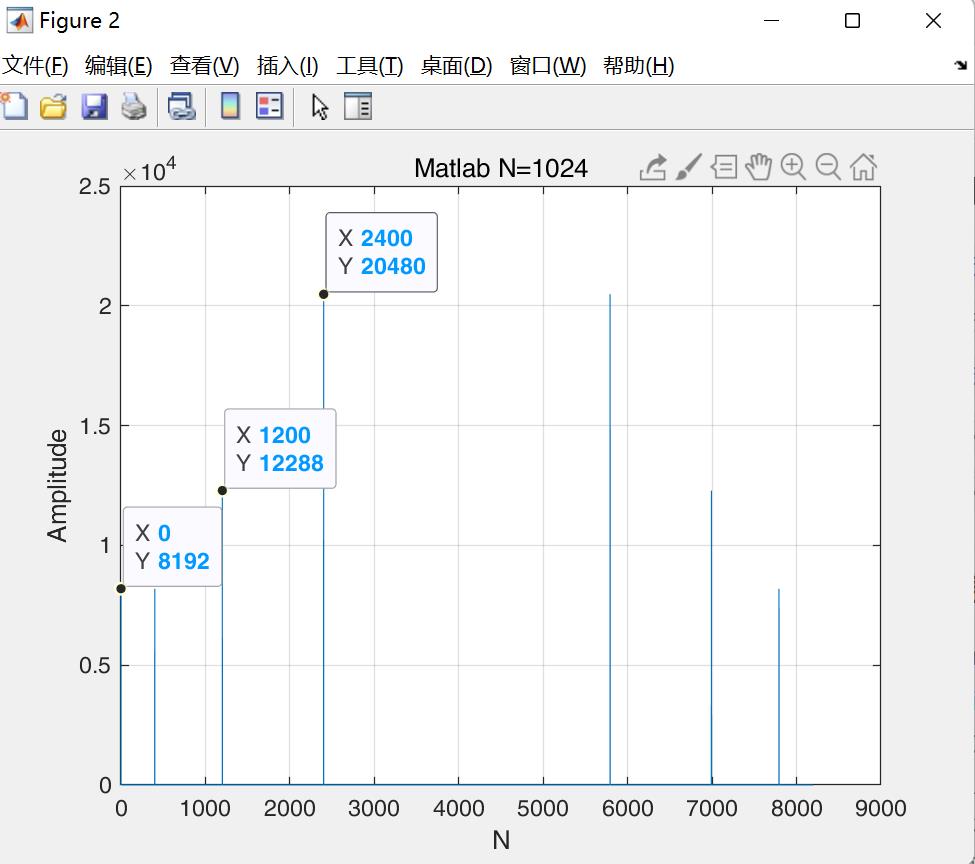
而每个点的相位呢,就是在该频率下的信号的相位。第一个点表示直流分量(即0Hz),而最后一个点N的再下一个点(实际上这个点是不存在的,这里是假设的第N+1个点,也可以看做是将第一个点分做两半分,另一半移到最后)则表示采样频率Fs,这中间被N-1个点平均分成N等份,每个点的频率依次增加。
例如某点n所表示的频率为:Fn=(n-1)*Fs/N。
由上面的公式可以看出,Fn所能分辨到频率为为Fs/N,如果采样频率Fs为1024Hz,采样点数为1024点,则可以分辨到1Hz。 1024Hz的采样率采样1024点,刚好是1秒,也就是说,采样1秒时间的信号并做FFT,则结果可以分析到1Hz,如果采样2秒时间的信号并做FFT,则结果可以分析到0.5Hz。
如果要提高频率分辨力,则必须增加采样点数,也即采样时间。
频率分辨率和采样时间
频率分辨率和采样时间是倒数关系。
clc;close all;clear all;
Fs=48000; %采样频率 即频率分辨率
N=48000; %采样点数
f1=50;
f2=750;
T=1/Fs; %采样时间
t=(0:1:N-1)*T;
% y=2+3*sin(2*pi*f1*t-pi*30/180)+1.5*sin(2*pi*f2*t+pi*90/180); %生成输入信号
y=0.1*sin(2*pi*f1*t)+0.1*sin(2*pi*f2*t);
figure(1)
plot(t, y);
filename = 'sine.wav';
audiowrite(filename, y, Fs);
Y = fft(y, N); %作FFT变换
A = abs(Y); %计算幅值
figure(2)
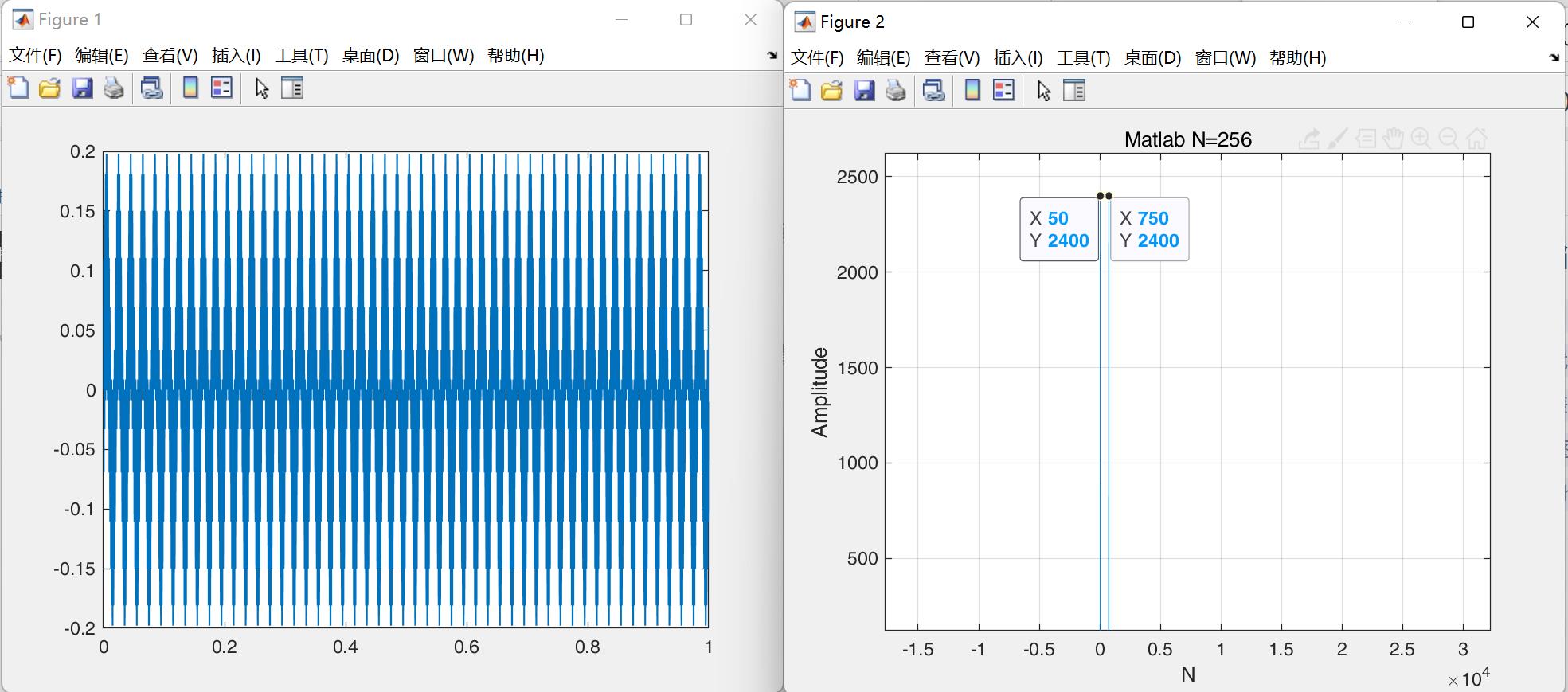
plot(0:1:(N-1), A);title('Matlab N=256');xlabel('N');ylabel('Amplitude');%作图
grid on
通过一个例子可以比较清晰的验证,若采样频率Fs=48k和采样点N=48k数值一致。
对于正弦分量 0.1* sin(2* pi* f2* t)中的 t 含义如下
t = 时间序号(即采样点序号)* 采样时间间隔 = n* T = n/Fs = 采样点序号 / 采样频率
所以,总采样时间t = 48k/48k = 1s,即实现采1秒钟数据
此时对于采样频率 采样点在频谱图中的反应又会发生什么变换呢?
采样间隔和采样频率既然是一一对应,,那么原本第一个时域采样点对应频域第一个采样频率,依然是第一个时域采样点对应第一个频域采样频率
有了上面的详细分析,现在继续套用之前的公式来理解,某点n所表示的频率为:Fn = ( n - 1 ) * Fs / N
即采1秒钟数据,分辨率达到1Hz。
若采样频率Fs=48k,而采样点N=48k * 2,因为,采样时间间隔是T= 1/Fs,也就是每隔T就会在频谱图中对应时域的对应采样点的一个频率值
对于正弦分量 0.1* sin(2* pi* f2* t)中的 t 含义如下
t = 时间序号(即采样点序号)* 采样时间间隔 = n* T = n/Fs = 采样点序号 / 采样频率
所以,总采样时间t = 2s,即实现采2秒钟数据
此时对于采样频率 采样点在频谱图中的反应又会发生什么变换呢?
采样间隔从上面1秒钟采样的例子中的 t = n / 48k n=[0, 48k],变成了 T = n / 48k n=[0, 48k*2],采样间隔增加了一倍,那么原本第一个时域采样点对应频域第一个采样频率,现在变成了第一个时域采样点对应第二个频域采样频率
有了上面的详细分析,现在继续套用之前的公式来理解,某点n所表示的频率为:Fn = ( n - 1 ) * Fs / N
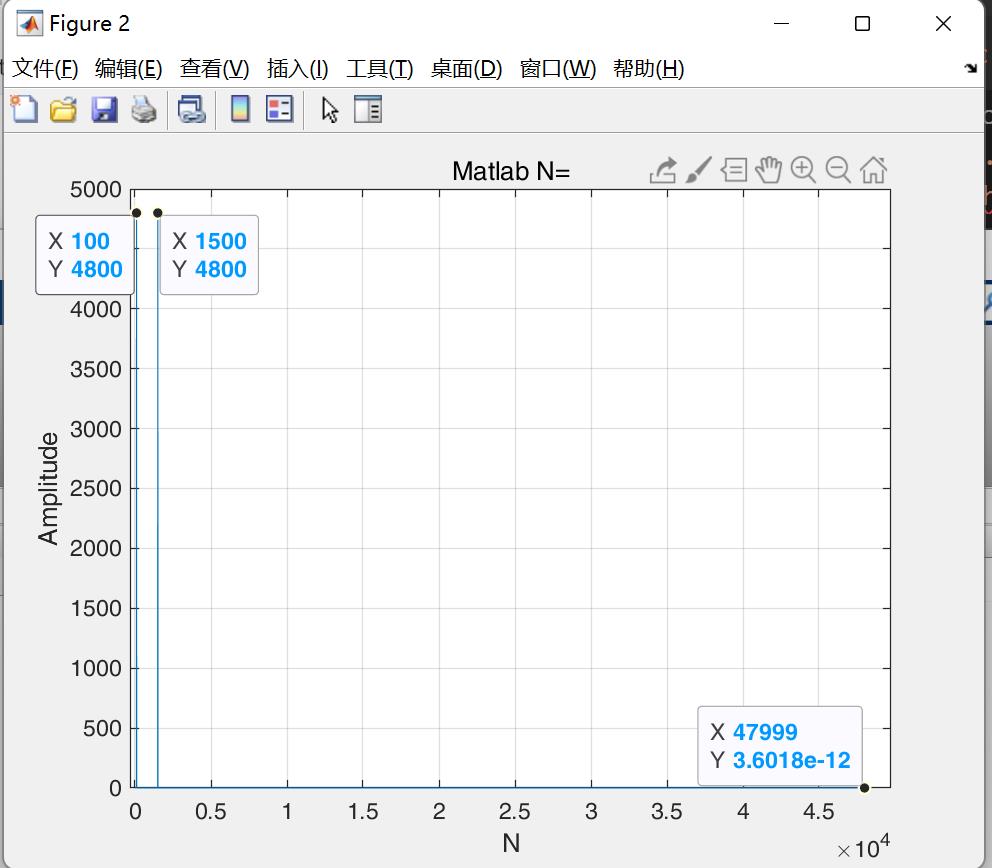

采样点
在上面的信号分析中,只提到了时域中信号的采样频率,采样序列,对于fft中一个很重要的概念——采样点,其实没有说明。
对于fft的采样点,要和我们生成时域中正弦信号中的一些概念区别开来, fft的采样点,具体来说就是fft变换时实际参与的采样序列的数量
因为我们上面的程序中信号和分析都是自己处理,所以就生成了多少点,然后就对多少点进行了fft
为了方便进行FFT运算,这个采样点通常N取2的整数次方
如何决定要使用多少点来做FFT?
在实际中,我们假设实际的信号长度为48000* 10,那么我们fft其实没有必要取全部的点
首先,fft函数出来的应该是个复数,每一个点分实部虚部两部分。假设采用1024点fft,采样频率是fs,那么第一个点对应0频率点,第512点对应的就是 512 * fs/1024 = fs / 2 的频率点。
FFT点数N(也就是离散时间信号的记录长度):要根据所要求的的频率分辨率Fn来决定。
频率分辨率F:能够用FFT算法分析得到的最靠近的两个信号频率之间的间隔F=Fs/N,也就是最小是能分辨到1还是0.5还是其他,1就代表时域中序列的一个点对应频域中序列的一个点,0.5就代表时域中序列的一个点对应频域中序列的两个点,显然后者在频域中的精度更加的高,也就是频率的分辨率更加的高。
对于采样点N和频率分辨率F的关系:N >= Fs / F, Fs为采样频率。
由于FFT一般要求N是2的整数幂,所以最后还要把FFT的采样点N扩大为最接近2的整数幂。
实例FFT采样点分析
还是用一个实例来进行说明
首先也是生成一个y=2+6*sin(2*pi*f1*t-pi*30/180)+2*sin(2*pi*f2*t+pi*90/180)+2*sin(2*pi*f3*t+pi*60/180);作为输入信号
其中这个输入信号的采样频率Fs是48k,序列的长度N是48k*2
FFT采样点的选择根据上面的分析 N >= Fs / F,如果我们需要的频率分辨率为10,那么也就是采样点N大于等于48k即可,这里我们选择采样点N为8192。
上述分析具体到matlab程序中参数名称有所变化,请注意!
clc;close all;clear all;
M=8192;%fft采样点
Fs=48000; %采样频率,一秒多少个采样点
N=48000*2; %序列长度,总数据有多少个点,即对N个点FFT
f1=50;
f2=750;
f3=1500;
T=1/Fs; %单个点采样时间
t=(0:1:N-1)*T; %总时间T/Fs,每个点时间间隔t
y=2+6*sin(2*pi*f1*t-pi*30/180)+2*sin(2*pi*f2*t+pi*90/180)+2*sin(2*pi*f3*t+pi*60/180); %生成输入信号
% y=0.1*sin(2*pi*f1*t+pi/3)+0.2*sin(2*pi*f2*t-pi/6);
figure(1)
plot(t, y);
% 存储信号到wav文件
% filename = 'sine.wav';
% audiowrite(filename, y, Fs);
% Matlab FFT
Y = fft(y, M); %作FFT变换
A = abs(Y); %计算幅值
figure(2)
% plot(0:1:(N-1)/2, A(1:N/2));
plot(0:1:M-1, A(1:M));title('Matlab N=8192');xlabel('N');ylabel('Amplitude');%作图
grid on

图中可以比清晰的看到,这次我们的fft点数为8192个
信号幅度分析
假设FFT之后某点n用复数a+bi表示,那么这个复数的模就是An=根号aa+bb,相位就是Pn=atan2(b,a)。根据以上的结果,就可以计算出n点(n≠1,且n<=N/2)对应的信号的表达式为:
An / (N/ 2) * cos(2 * pi* Fn* t+Pn),即 2* An/N* cos(2* pi* Fn* t+ Pn)。
对于n=1点的信号,是直流分量,幅度即为A1/N。
由于FFT结果的对称性,通常我们只使用前半部分的结果,即小于采样频率一半的结果。
下面以一个实际的信号来详细做说明。
假设我们有一个信号,它含有2V的直流分量,频率为50Hz、相位为-30度、幅度为3V的交流信号,以及一个频率为75Hz、相位为90度、幅度为1.5V的交流信号。用数学表达式就是如下:
y=2+3*cos(2*pi*f1*t-pi*30/180)+1.5*cos(2*pi*f2*t+pi*90/180);
式中cos参数为弧度,所以-30度和90度要分别换算成弧度。
我们以256Hz的采样率对这个信号进行采样,总共采样256点。按照我们上面的分析,Fn=(n-1)*Fs/N,我们可以知道,每两个点之间的间距就是1Hz,第n个点的频率就是n-1。
clc;close all;clear all;
Fs=256;
T=1/Fs;
N=256;
f1=50;
f2=75;
t=(0:1:N-1)*T;
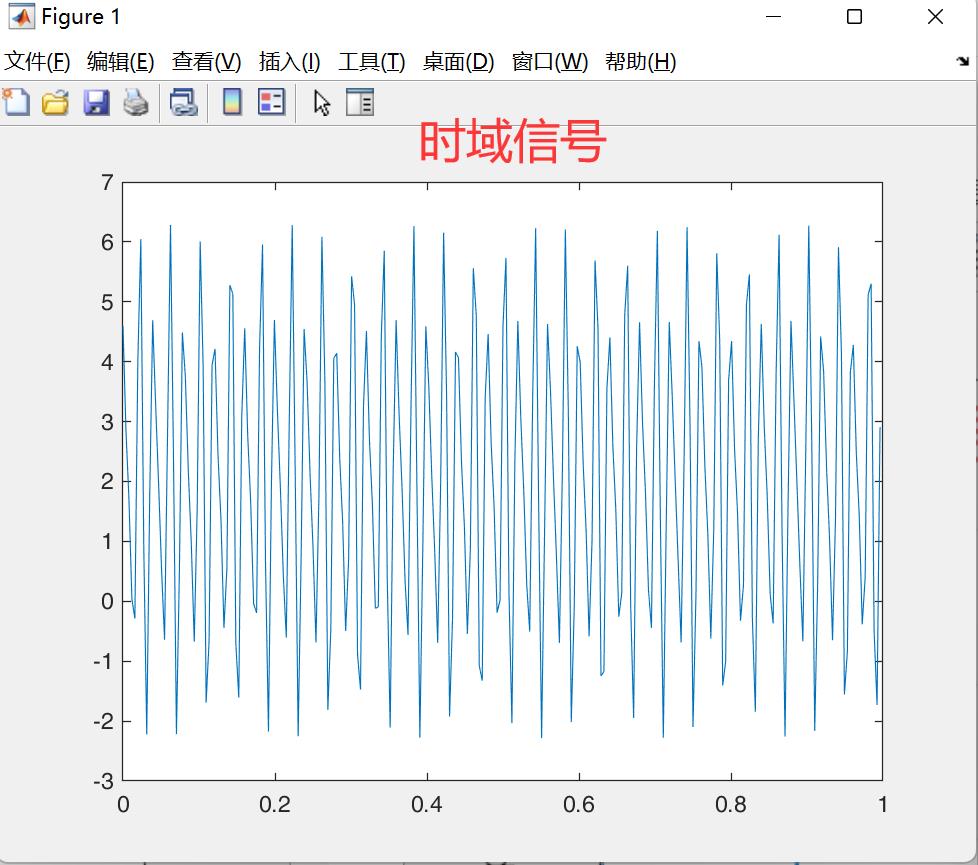
y=2+3*cos(2*pi*f1*t-pi*30/180)+1.5*cos(2*pi*f2*t+pi*90/180); %生成输入信号
figure(1)
plot(t, y);
% filename = 'sine.wav';
% audiowrite(filename, y, Fs);
Y = fft(y, N); %作FFT变换
A = abs(Y); %计算幅值
figure(2)
plot(0:1:(N-1), A);title('Matlab N=256');xlabel('N');ylabel('Amplitude');%作图
grid on
我们的信号有3个频率:0Hz、50Hz、75Hz,应该分别在第0个点、第50个点、第75个点上出现峰值,其它各点应该接近0。
实际情况如何呢?我们来看看FFT的结果的模值如图所示。
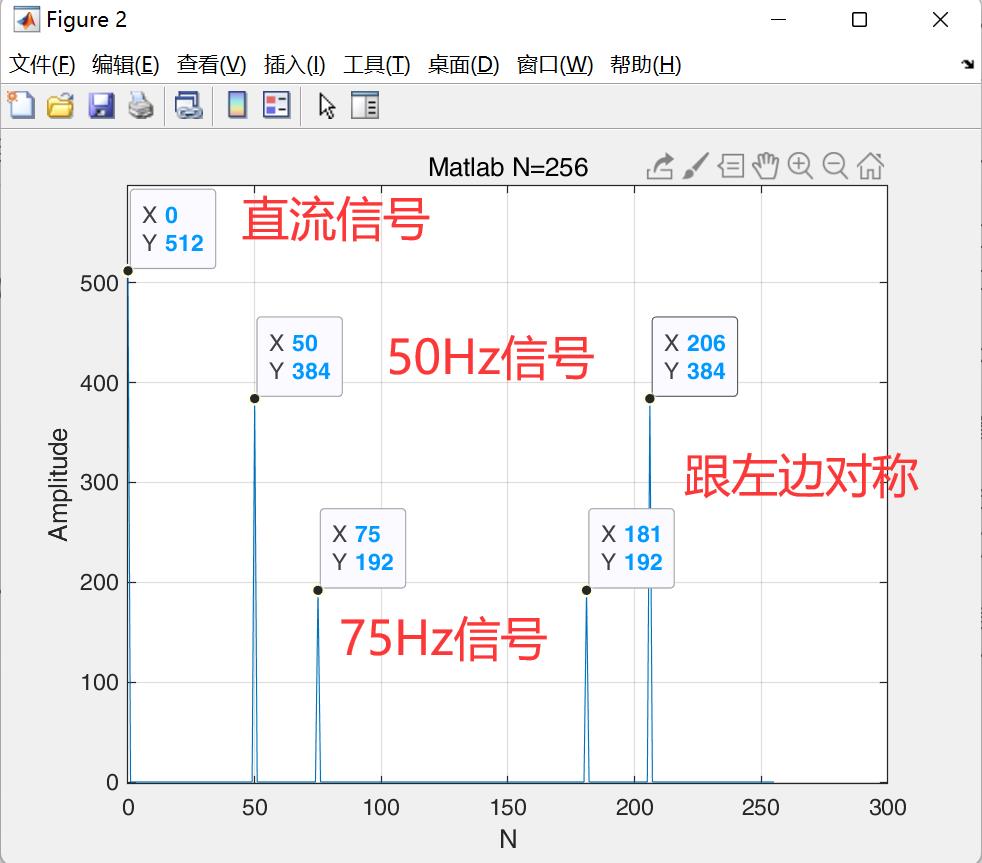
幅度分析
从图中我们可以看到,在第0点、第50点、和第75点附近有比较大的值(注意:因为plot作图习惯的原因,把第一个点定义为了0点)。我们分别将这三个点附近的数据拿上来细看:

0点: 5.119999999999999e+02 + 0.000000000000000e+00i
1点: -2.596032278819034e-14 - 1.428167681322866e-13i
2点: -2.797762022055395e-14 - 1.407762795224699e-13i
49点:-1.249148148486610e-12 + 6.534772133137322e-13i
50点:-6.205653671318325e-13 - 2.170294576875076e-12i
51点:3.325537550532247e+02 - 1.919999999999996e+02i
74点:8.230832814121277e-14 - 4.724619872104589e-13i
75点:-2.185335025085591e-13 - 1.015196857708225e-12i
76点:3.439777178218570e-12 + 1.919999999999998e+02i
很明显,0点、50点、75点的值都比较大,它附近的点值都很小,可以认为是0,即在那些频率点上的信号幅度为0。接着,我们来计算各点的幅度值。分别计算这三个点的模值,结果如下:
0点: 512
50点:384
75点:192
按照公式,可以逆向计算,计算出时域中
直流分量为:
512/N = 512/256 = 2;
50Hz信号的幅度为:
384/(N/2) = 384/(256/2) = 3;
75Hz信号的幅度为
192/(N/2) = 192/(256/2) = 1.5。
可见,对照时域的幅度,从频谱分析出来的幅度是正确的。
然后再来计算相位信息。直流信号没有相位可言,不用管它。
先计算50Hz信号的相位,atan2(-192, 332.55)=-0.5236,结果是弧度,换算为角度就是180*(-0.5236)/pi=-30.0001。
再计算75Hz信号的相位,atan2(192, 3.4315E-12)=1.5708弧度,换算成角度就是180*1.5708/pi=90.0002。
可见,相位也是对的。根据FFT结果以及上面的分析计算,我们就可以写出信号的表达式了,它就是我们开始提供的信号。
FFT总结: 假设采样频率为Fs,采样点数为N,做FFT之后
- FFT后某一点n(n从1开始)表示的频率为:Fn=(n-1)*Fs/N;
- 该点的模值除以N/2就是对应该频率下的信号的幅度(对于直流信号是除以N);
- 该点的相位即是对应该频率下的信号的相位。相位的计算可用函数atan2(b,a)计算。atan2(b,a)是求坐标为(a,b)点的角度值,范围从-pi到pi。
要精确到xHz,则需要采样长度为1/x秒的信号,并做FFT。
要提高频率分辨率,就需要增加采样点数,这在一些实际的应用中是不现实的,需要在较短的时间内完成分析。解决这个问题的方法有频率细分法,比较简单的方法是采样比较短时间的信号,然后在后面补充一定数量的0,使其长度达到需要的点数,再做FFT,这在一定程度上能够提高频率分辨力。具体的频率细分法可参考相关文献。
ARM FFT 时域、频域分析
Matlab有了原理的验证和解释,下面就是移植到ARM平台进行验证
依然是与上例中各项参数保持一致
#include "stdio.h"
#include "math.h"
#define PI 3.1415926535
void kfft(double pr[], double pi[], int n, int k, double fr[], double fi[])
{
int it, m, is, i, j, nv, l0;
double p, q, s, vr, vi, poddr, poddi;
for (it = 0; it <= n-1; it++) { //将pr[0]和pi[0]循环赋值给fr[]和fi[]
m = it;
is = 0;
for(i = 0; i <= k-1; i++) {
j = m / 2;
is = 2 * is + (m - 2 * j);
m = j;
}
fr[it] = pr[is];
fi[it] = pi[is];
}
pr[0] = 1.0;
pi[0] = 0.0;
p = 6.283185306 / (1.0 * n);
pr[1] = cos(p); //将w=e^-j2pi/n用欧拉公式表示
pi[1] = -sin(p);
for(i = 2; i <= n-1; i++) { //计算pr[]
p = pr[i - 1] * pr[1];
q = pi[i - 1] * pi[1];
s = (pr[i - 1] + pi[i - 1]) * (pr[1] + pi[1]);
pr[i] = p - q;
pi[i] = s - p - q;
}
for(it = 0; it <= n-2; it = it + 2) {
vr = fr[it];
vi = fi[it];
fr[it] = vr + fr[it + 1];
fi[it] = vi + fi[it + 1];
fr[it + 1] = vr - fr[it + 1];
fi[it + 1] = vi - fi[it + 1];
}
m = n / 2;
nv = 2;
for(l0 = k - 2; l0 >= 0; l0--) { //蝴蝶操作
m = m / 2;
nv = 2 * nv;
for(it = 0; it <= (m - 1) * nv; it = it + nv)
for (j = 0; j <= (nv / 2) - 1; j++) {
p = pr[m * j] * fr[it +j + nv / 2];
q = pi[m * j] * fi[it +j + nv / 2];
s = pr[m * j] + pi[m * j];
s = s * (fr[it + j + nv / 2] + fi[it + j + nv / 2]);
poddr = p - q;
poddi = s - p - q;
fr[it + j + nv / 2] = fr[it + j] - poddr;
fi[it + j + nv / 2] = fi[it + j]以上是关于从Matlab平台进行FFT到ARM平台C语言FFT频谱分析的主要内容,如果未能解决你的问题,请参考以下文章
移植 libevent-2.0.22-stable 到ARM平台