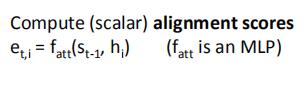机器学习笔记： attention

Posted 2021-12-07 UQI-LIUWJ

1 回顾： 使用RNN的Seq2Seq

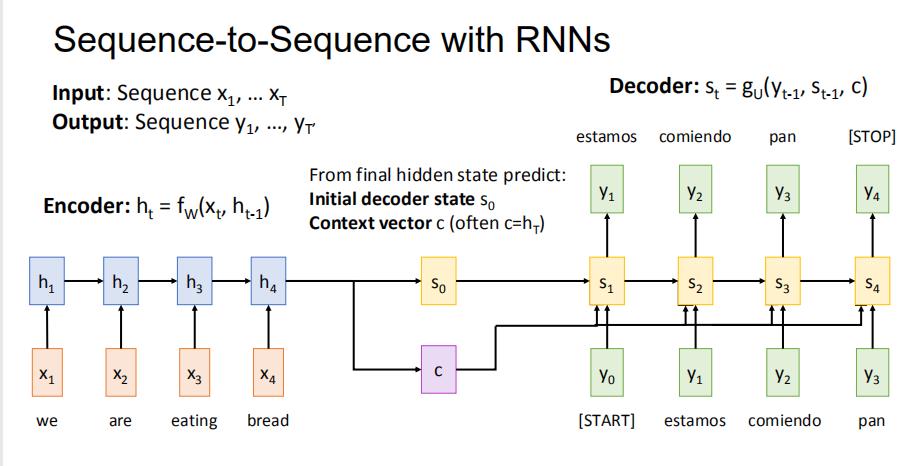
        encoder最后的输出，我们生成两个向量，初始的decoder状态s0和文本向量c。然后进行decoder操作         

        但是问题在于，如果输入的sequence很长的话，可能我们fixed的文本向量c不够灵活。毕竟输出不用看所有输入，只需要看相关的输入即可

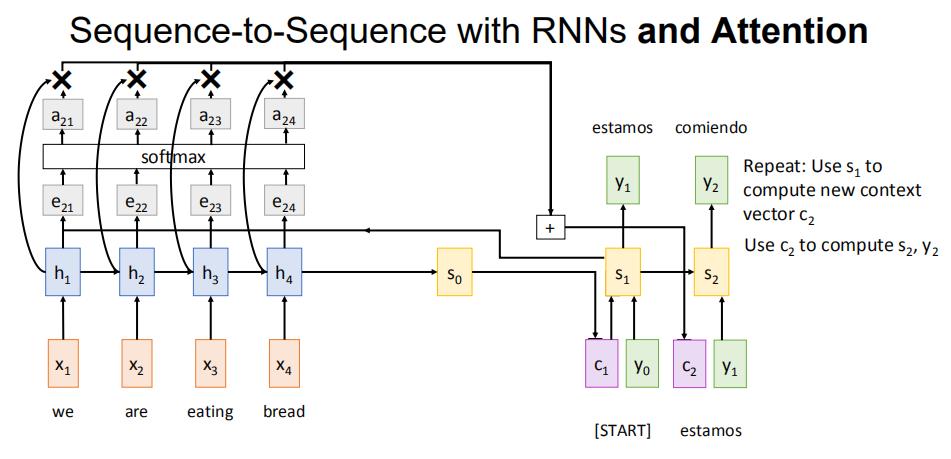
2 seq2seq 使用RNN和attention模块

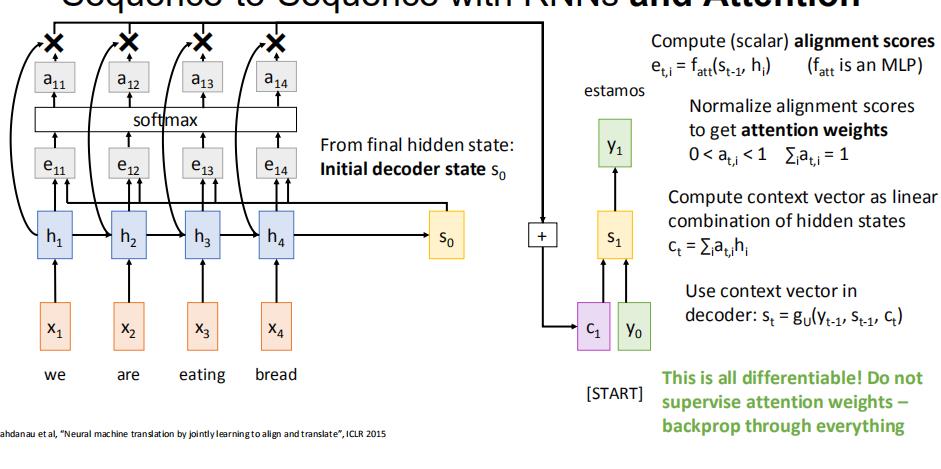
于是我们在seq2seq模型中添加attention模块

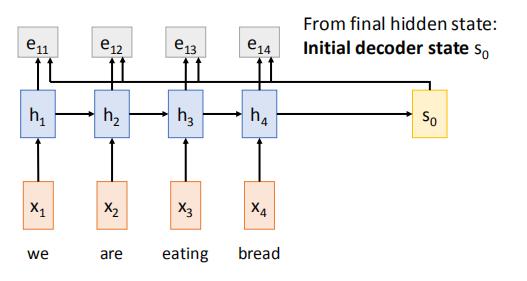
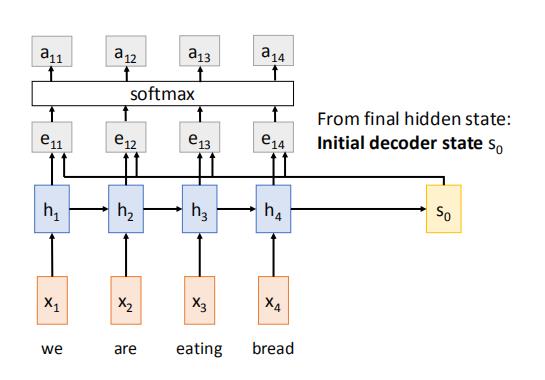
首先，对于encoder的输出，我们将其与之前的隐状态h一起送入MLP，得到对齐值e

 然后我们使用softmax模块，将e归一化为[0,1]，且和为1的注意力权重a

 之后我们将h与相对应的权重a相乘，再求和，得到此时的文本向量c1

然后使用上一轮的s，本轮的c，以及本轮decoder的输入y，生成本轮的状态s‘

 下一轮，使用s1进行计算，然后得到c2.....以此类推

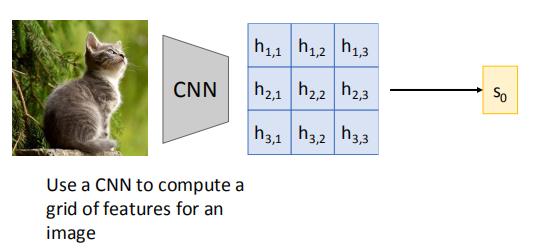
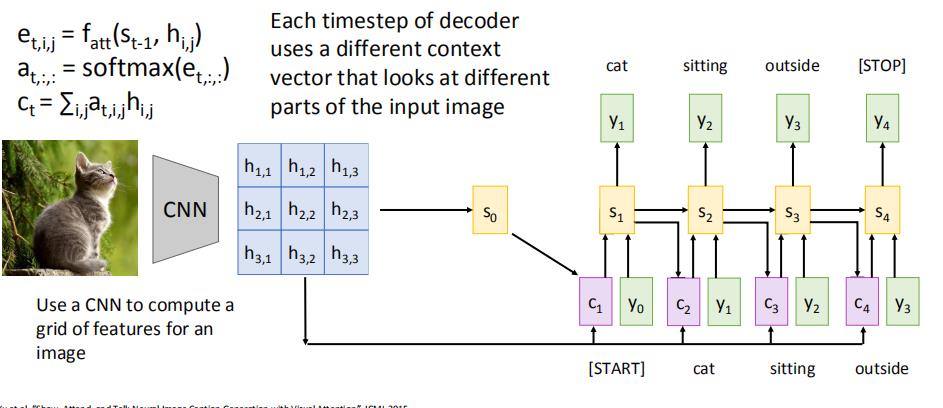
 2.1 举例：RNN & attention 用于图片注明

首先，图片经过CNN得到一个矩阵，然后矩阵通过某些神经网络，得到一个状态s0

 

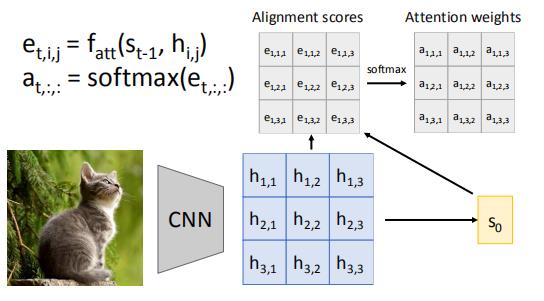
然后，用s0和h的每个条目， 分别计算一个e

 

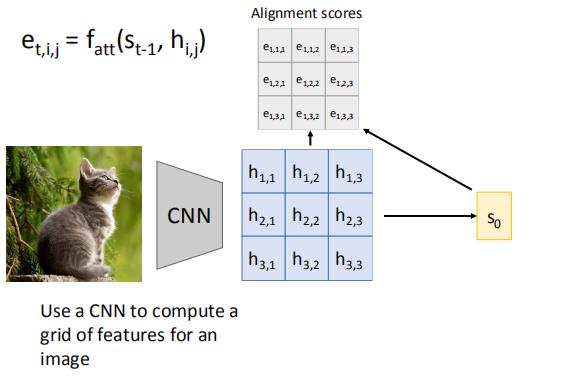
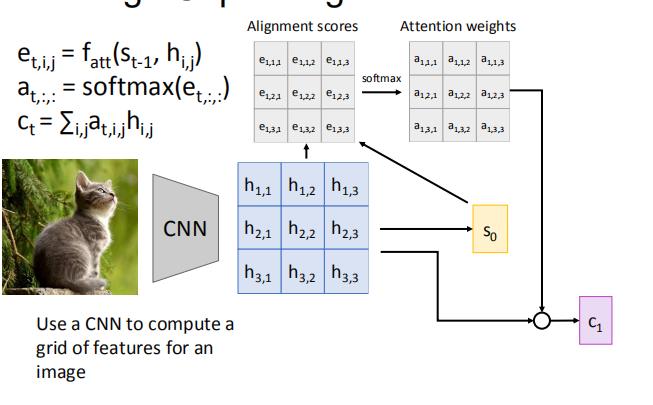
 之后经过attention，得到权重值

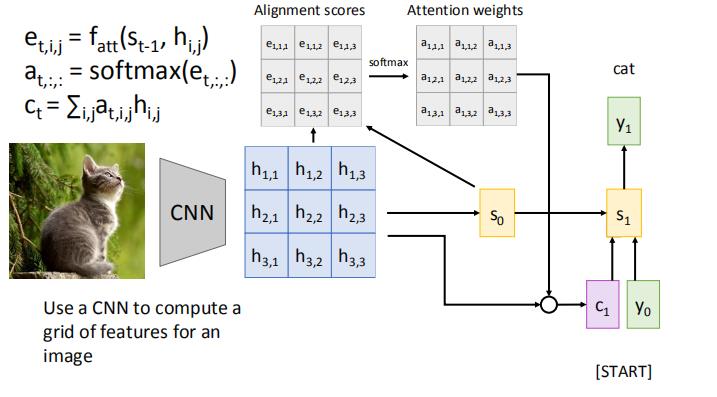
h和对应的a乘积求和，得到c

 s0,c1,y0计算，得到s1

 再将s1送进去，以此循环：

 3 attention 层

这是我们上一小节的attention，我们对其做一个改动

	attention in Seq2seq	attention layer
query	s	Query vector : q (Shape: )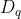
input	h矩阵	Input vectors : X (Shape: )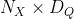
相似度方法 （e的求法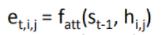）		q和X的点积
计算流程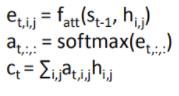

 说一下这里除以根号D的原因：比较大的相似度会使得softmax层饱和，这会导致梯度消失，除以根号D的作用就是在一定程度上约束相似度，缓解梯度消失的问题。（q和x维度越大，内积的结果也应该越大，所以需要除以一个和维度正相关的参数。）

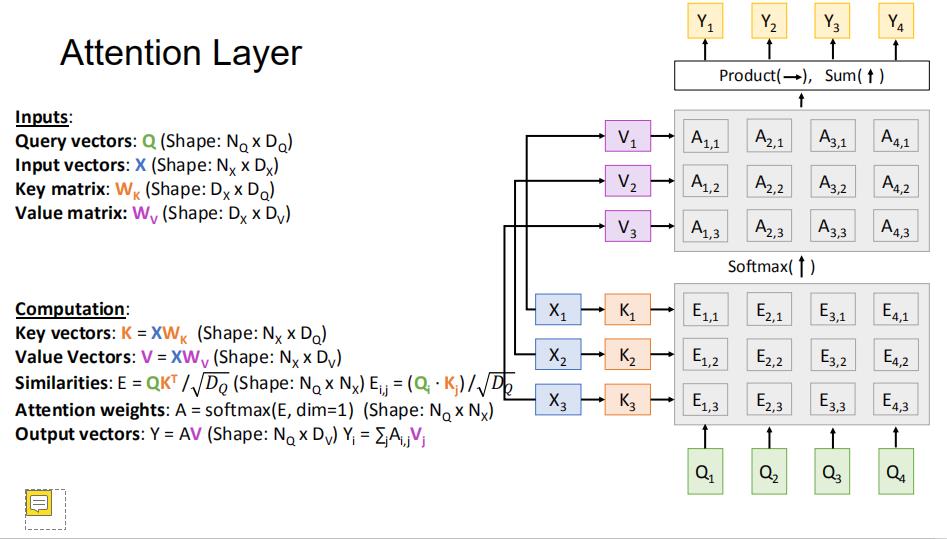
当然，我们也可以这么表示 attention layer

 

 这里的Q是外部的矩阵

 

 4 self-attention

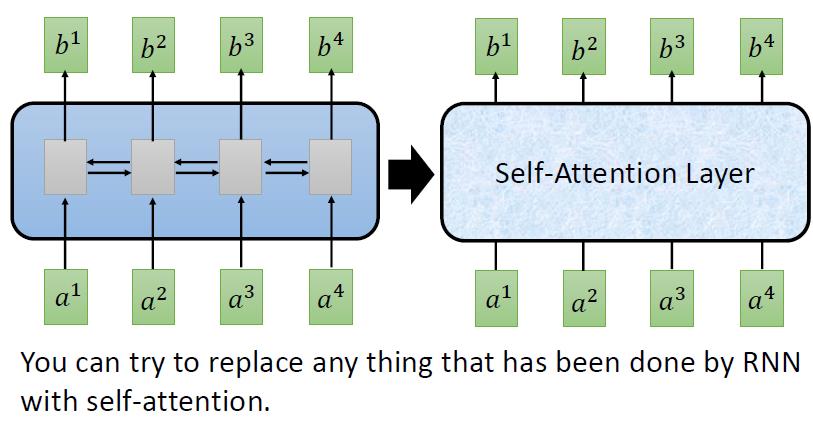
像比于attention layer，self-attention layer 没有外来的Q，Q得自己求得

 它可以代替bi-direction RNN，而且相比于RNN，self-attention layer可以并行

4.1 attention 步骤

->1，对于一个input xi，我们先经过一个embedding（乘以一个矩阵），使xi变成ai

->2，然后ai分别乘上三个不同的变化矩阵（transformation matrix），变成qi，ki，vi。

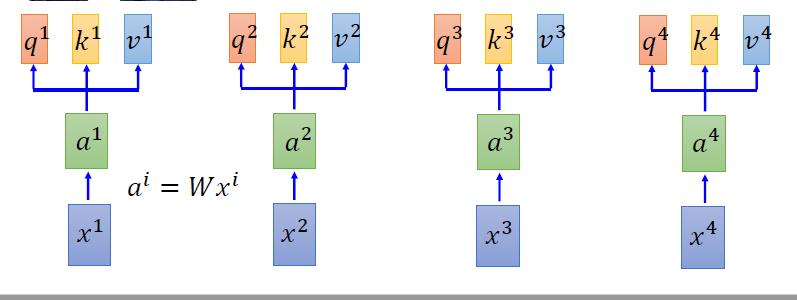
->3 得到Q,K,V之后，就和前面的一致了

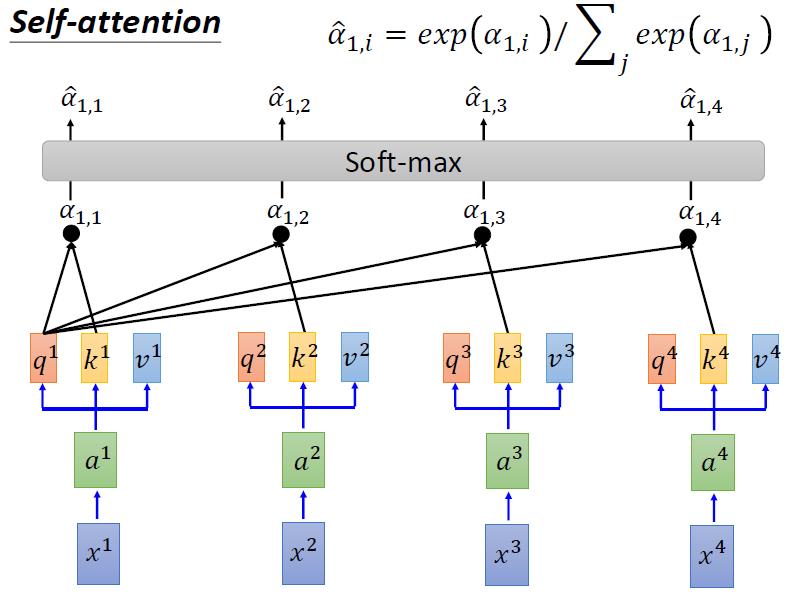
->4 将上一部算出来的结果进行softmax（使得和为1，每个值都在0~1之间）

-> 5  将第4步算出来的权重，和v1进行加权求和，得到的就是x1经过self-attention后对应的embedding结果

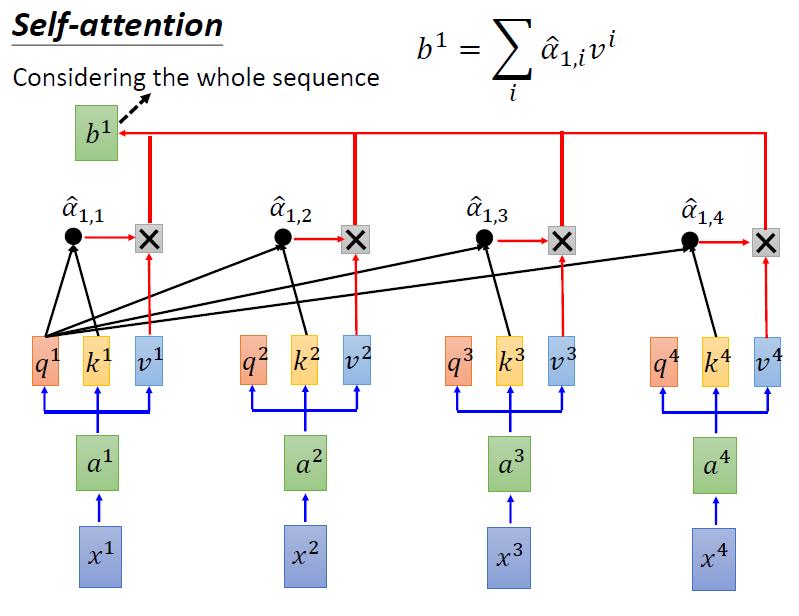
-> 6 同理，我们有b2~b4

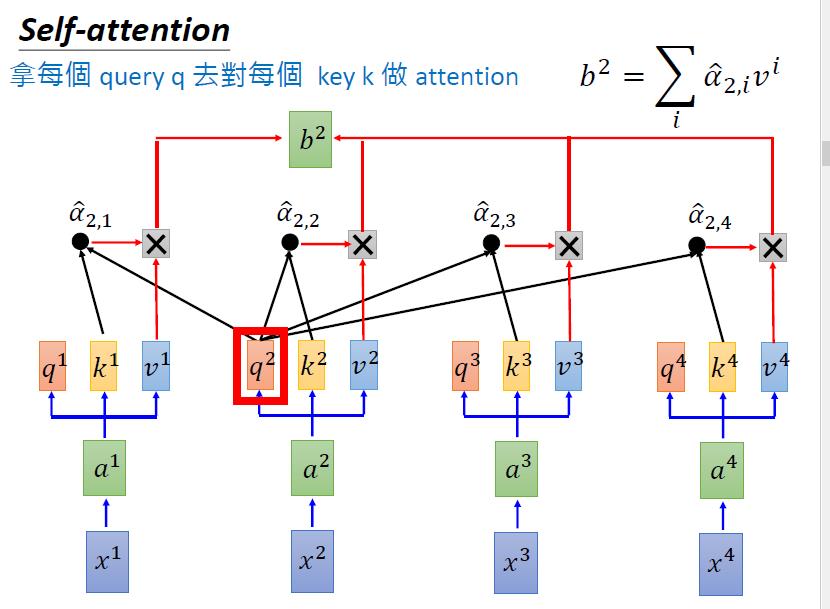
4.2  self-attention的优点

self-attention的好处是，每一个bi的输出，不仅综合考虑了所有input的情况；而且这个操作是可以并行运算的。

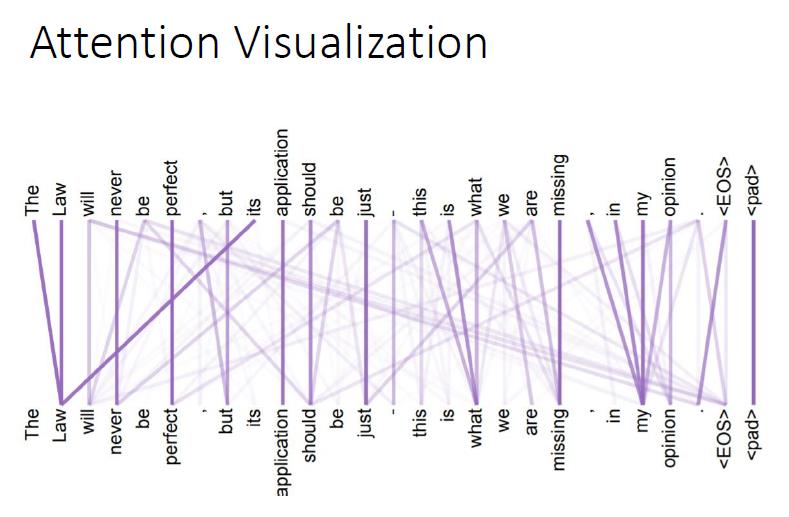
4.3 self-attention 可视化结果

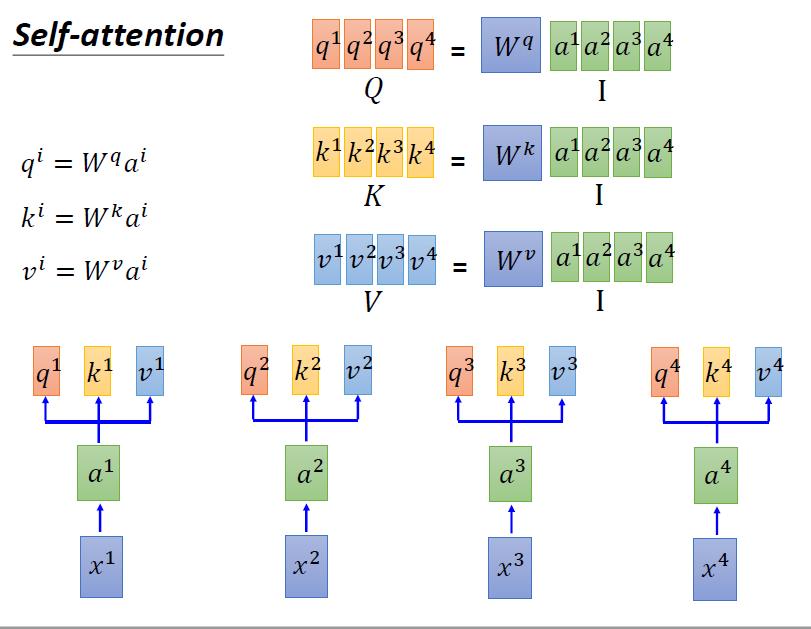
4.4 self-attention 矩阵表述

4.4.1 计算query、key、value 

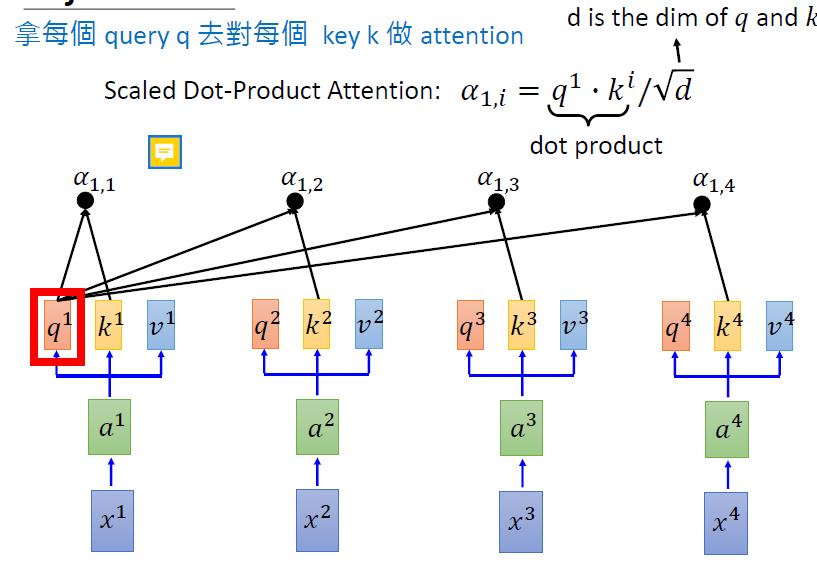
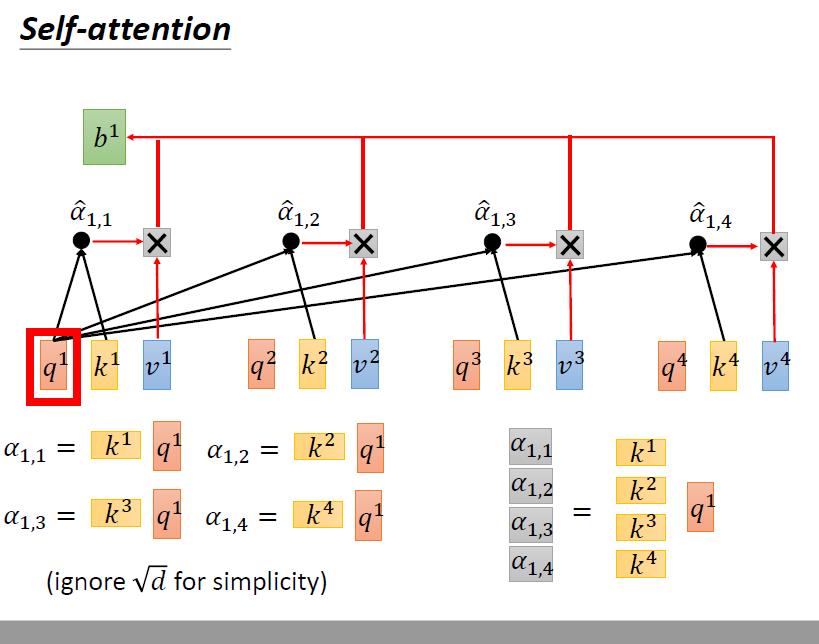
4.4.2 计算 a1i

为了简化，我们把所有的除以根号d都省略了

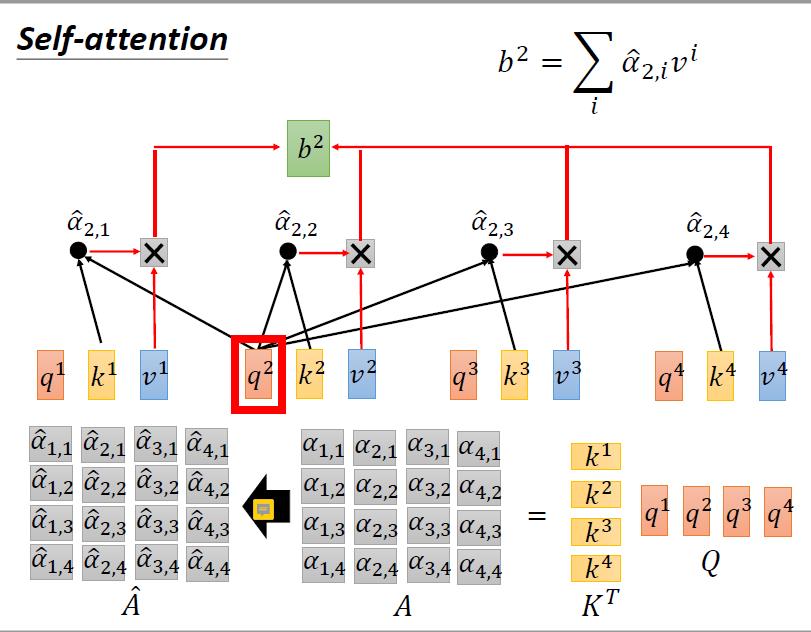
4.4.3 计算整个的a

然后对每一列进行softmax操作

4.4.4 计算 b

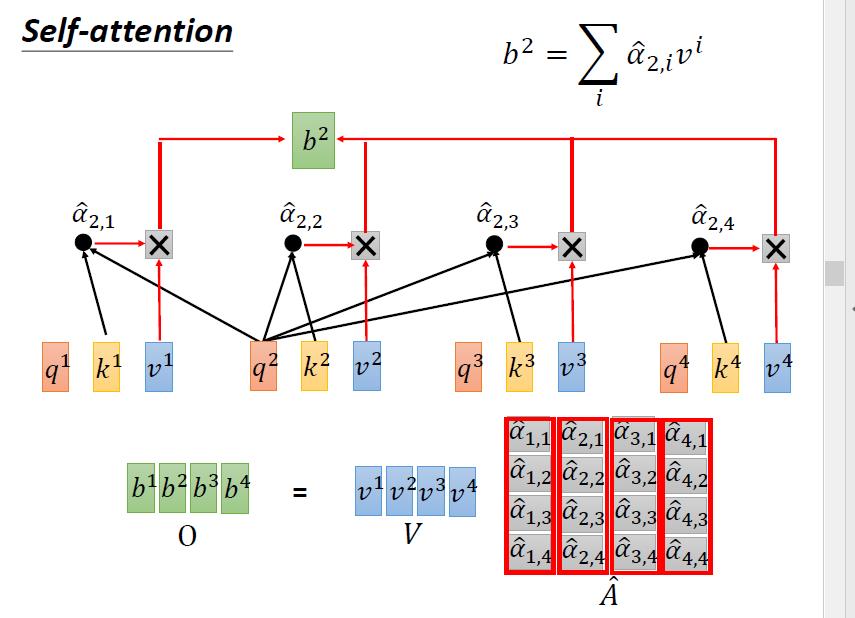
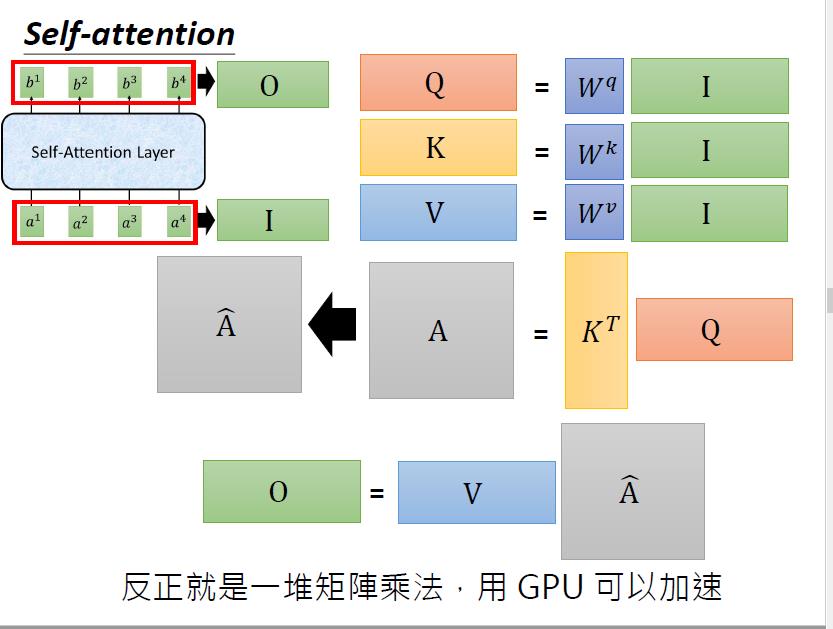
4.4.5 总览

 

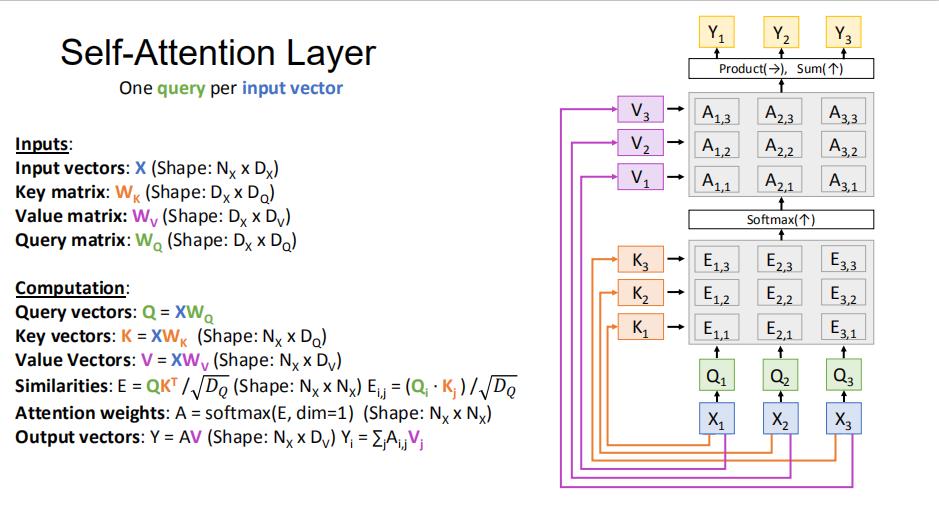
4.5 multi-head self-attention

4.5.1 multi-head self-attention 原理

 大体思路和self-attention是一样的。不同之处在于，我们得到q,k,v后，我们用不同的方法再生成一组q,k,v。

 进行self-attention的时候，每一种办法生成的qki之和自己这种办法生成的qki进行操作

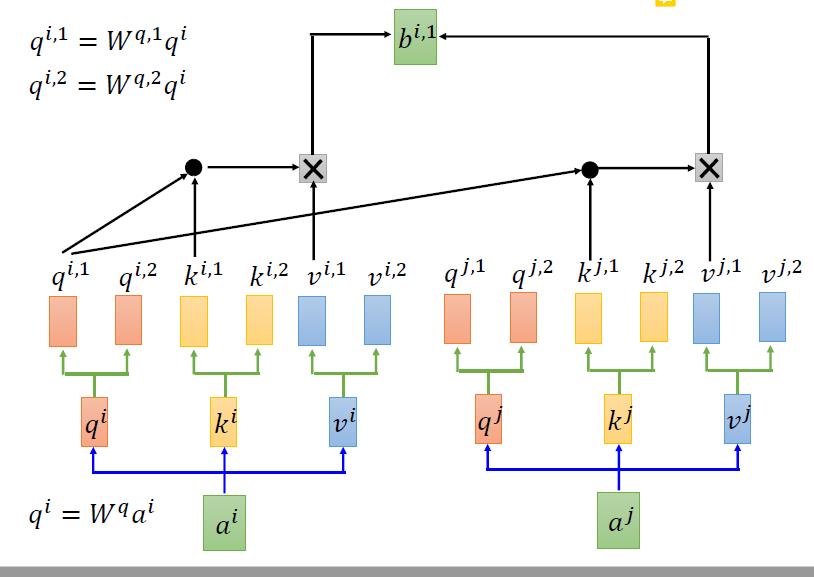
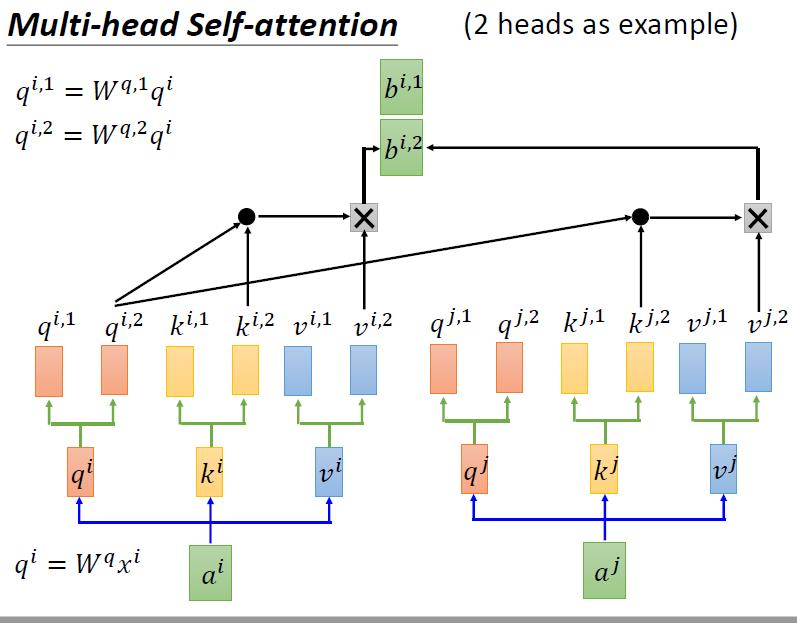
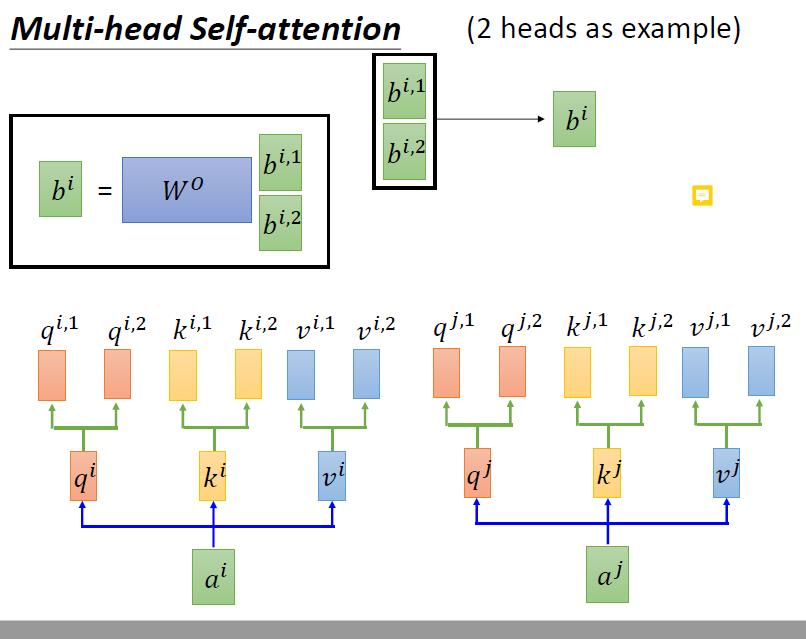
然后这两个bi再通过某种方式merge成一个b 

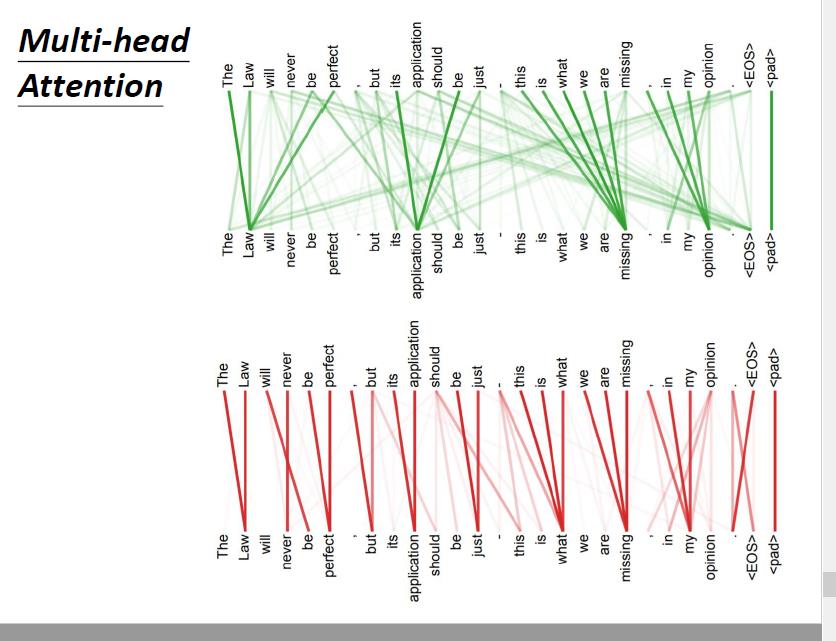
4.5.2 multi-head self-attention可视化

越粗表示之间的权重越大，关系越近。

我们可以发现，不同的head侧重点是不一样的：一个注重距离上的远近，一个关注语义上的远近

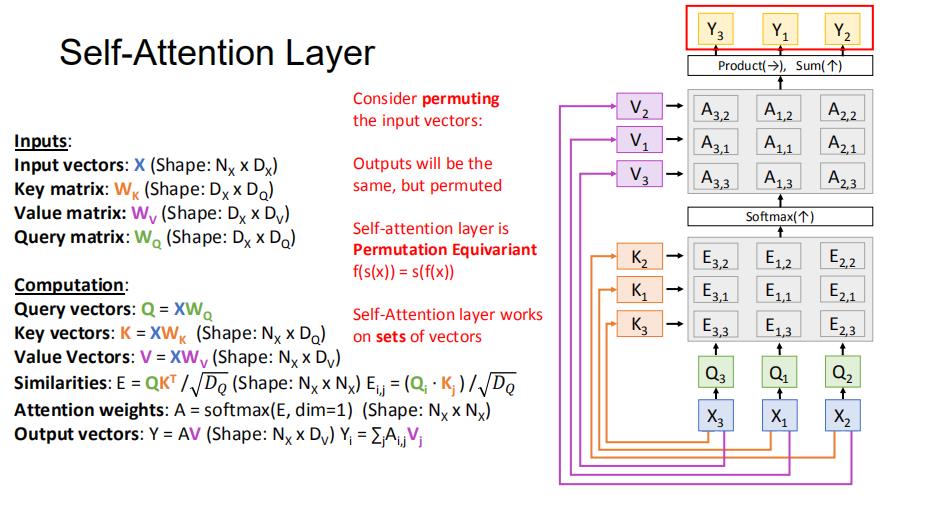
4.6 排列不变性与位置编码

        假设我们改变输入X的排列顺序，最终的输出只是也改变了排列的顺序，但是内容不会因为排列的变化而发生改变。我们称这个为排列不变性

 

 倘若我们不需要排列不变性的话，我们可以对每一个输入叠加一段位置编码，这样排列不变性就被破坏了

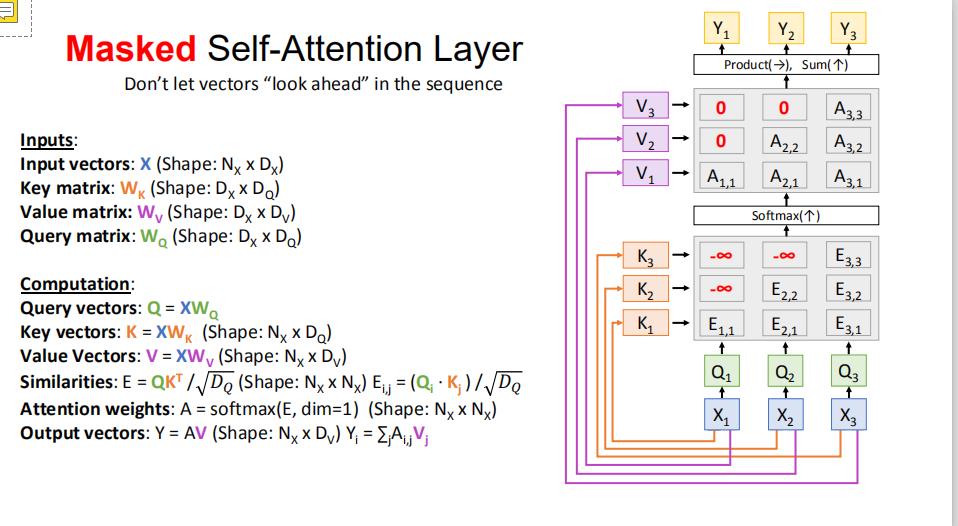
4.7 masked self-attention

中心思想就是，我们只考虑过去的内容对我的attention权重

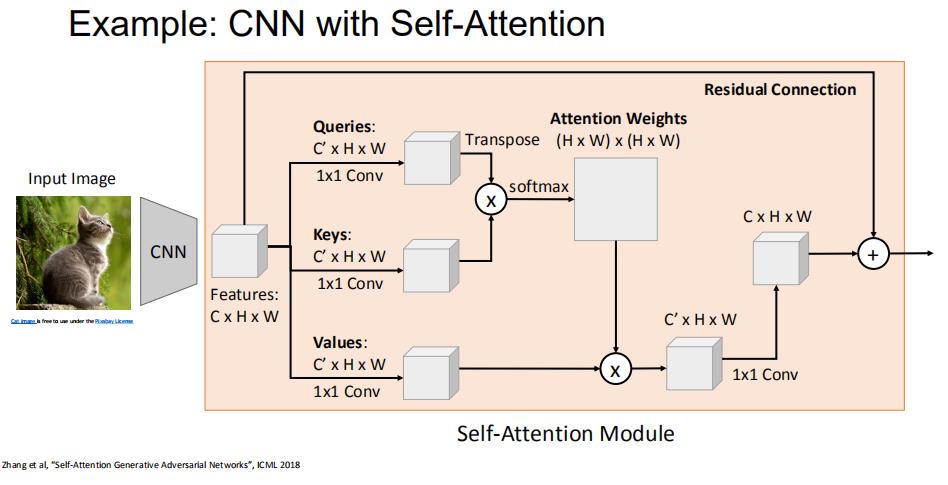
 4.8 CNN+self-attention