(王道408考研数据结构)第一章绪论-第二节2：算法的时间复杂度和空间复杂度

Posted 2021-12-07 我擦了DJ

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了(王道408考研数据结构)第一章绪论-第二节2：算法的时间复杂度和空间复杂度相关的知识，希望对你有一定的参考价值。

文章目录

一：算法的时间复杂度
二：算法的空间复杂度

一：算法的时间复杂度

我们常常说：提高算法的效率，这里的效率多数情况下指的就是算法的执行时间，那么如何度量呢？

（1）事后统计方法

事后统计方法： 通过设计好的测试程序和数据，利用计算机计时器对不同算法编址的程序的运行时间进行比较，从而确定算法效率的高低。这种算法很明显有很大缺陷

事先编制程序，这本就是费时费力的举动，如果最后测试出来证明它是糟糕的算法，那岂不是“赔了夫人又折兵”吗
程序运行特别依赖于软件和硬件，不同的测试环境会掩盖算法效率的真实性。一个算法运行在超级计算机和运行在你的电脑上，其效率肯定是一个天上一个地下，这就不禁产生一个疑问，运行时间短的算法究竟是占了物理机运算速度优势还是说这个算法本身效率就很高？
算法的测试数据设计困难。我们常常说程序有bug，这些bug很多都是一些非常规的输入导致的，但是你编写程序不可能一开始就把所有情况都考虑齐全了

（2）事前分析估算的方法

事前分析估算：在计算机程序编制之前，依据统计方法对算法进行估算

我们发现，一个用高级程序语言编写的程序在计算机上运行消耗的时间常常取决于以下因素

算法采用的策略、方法
编译产生的代码质量
问题的输入规模
机器执行指令的速度

仍然以1+2+…+100为例，普通人的算法和高斯的算法区别如下

//普通人
int i,sum=0,n=100; //执行1次
for(i=1;i<=n;i++)//执行n+1次
{
	sum=sum+i;//执行n次
}
cout << sum;//执行1次

//大神高斯
int sum=0,n=100;//执行1次
sum=(1+n)*n/2;//执行1次
cout << sum//执行1次

显然普通人的算法一共执行了1+(n+1)+n+1=2n+3次，而高斯的算法执行了1+1+1=3次。这里我们把循环看作一个整体，两个算法其本质是n次和1次的差距，算法优劣之分显而易见

需要注意：我们分析程序的运行时间时，最重要的是要把程序看成独立于程序设计语言的算法或一系列步骤，不能束缚在特定的语言下考虑

比如下面的例子中

int i,j,x=0,sum=0,n=100;//执行一次
for(i=1;i<=n;i++)
{
	for(j=i;j<-n;j++)
	{
		x++;
		sum=sum+x;//执行了n×n次
	}
	cout << sum;//执行1次
}

x++和sum=sum+x在两个for循环的控制下要运行 $100^{2}$ 次，也就是 $n^{2}$ ，这个 $n$ 值我们称之为问题的规模， $n$ 越来越大，那么其在时间效率上的差异也就越来越大

对于高斯的算法，输入规模为 $n$ ，其操作的量数就为 $n$
对于刚才的那个例子，输入规模为 $n$ ，其操作的量数就为 $n^{2}$

（3）函数的渐进式增长

函数的渐进式增长：给定两个函数 $f (n)$ 和 $g (n)$ ，如果存在一个整数 $N$ ,使得对于所有的 $n$ > $N$ ， $f (n)$ 总是大于 $g (n)$ ，那么我们就说 $f (n)$ 的增长渐进快于 $g (n)$ （有种高数极限定义的味道）

比如下面几个算法的比较

次数	A1(2n+3)	A2(2n)	B1(3n+1)	B2(3n)
n=1	5	2	4	3
n=2	7	4	7	6
n=3	9	6	10	9
n=10	23	20	31	30
n=100	203	200	301	300

n=1时，A1效率不如B1
n=2时，A1效率等于B1
n>2时：A1效率开始优于B1
n越来越大，A1效率越来越好

还有一点，大家也可以发现，对于A2和B2算法后面都是没有常数，但是最终算法效率却大相近似，就像极限中的抓大头一样，我们完全可以忽略这些加法常数

再来看下面的比较

次数	C1(4 $n$ +8)	C2( $n$ )	D1(2 $n^{2}$ +1)	D2( $n^{2}$ )
n=1	12	1	3	1
n=2	16	2	9	4
n=3	20	3	19	9
n=10	48	10	201	100
n=100	408	100	20001	10000
n=1000	4008	1000	2000001	1000000

n<=3时，C1效率低于D1
n>3时，C1效率开始优于D1

而且大家还会发现这样的结论：即便去掉与最高次相乘的常数之后这样的效率关系也并不会改变

再来看下面的比较

次数	E1(2n $^{2}$ +3n+1)	E2(n $^{2}$ )	F1(2n $^{3}$ +3n+1)	F2( $n^{3}$ )
n=1	6	1	6	1
n=2	15	4	23	8
n=3	28	9	64	27
n=10	231	100	2031	1000
n=100	20301	10000	2000301	1000000

n=1时，E1和F1效率一样
n>1时，E1的效率开始优于F1

而且大家还会发现这样的结论：最高次项的指数大的，函数随着n的增长，结果也会增长特别快，其实判断一个算法的效率时，主要看最高次项的阶数，如果最高次为3，那么对于常数和低于3次的次项就不需要考虑了

（4）算法时间复杂度

A：算法时间复杂度定义-大 $O$ 记法

算法时间复杂度：在进行算法分析时，语句总的执行次数 $T (n)$ 是关于问题规模 $n$ 的函数，进而分析 $T (n)$ 随 $n$ 的变化情况并确定 $T (n)$ 的数量级。算法的时间复杂度也就是算法的时间量度，记作： $T (n) = O (f (n))$ 。它表示随问题规模 $n$ 的增大，算法执行时间的增长率和 $f (n)$ 增长率相同，称作算法的渐进时间复杂度，简称时间复杂度，其中 $f (n)$ 是问题规模 $n$ 的某个函数——这样用 $O ()$ 体现时间复杂度的方法称之为大 $O$ 记法

$O (1)$ 叫做常数阶
$O (n)$ 叫做线性阶
$O(n^{2})$ 叫做平方阶

B：推导大 $O$ 阶的方法

推导基本方法如下

用常数1取代运行时间中的所有加法常数
在修改后的运行次数函数中，只保留最高项数
如果最高项存在且不为1，则去除与这个项相乘的常数

其中：

$O (1)$ < $O(log_{2}n)$ < $O (n)$ < $O(nlog_{2}n)$ < $O(n^{3})$ < $O(2^{n})$ < $O (n!)$ < $O(n^{n})$ （常对幂指）

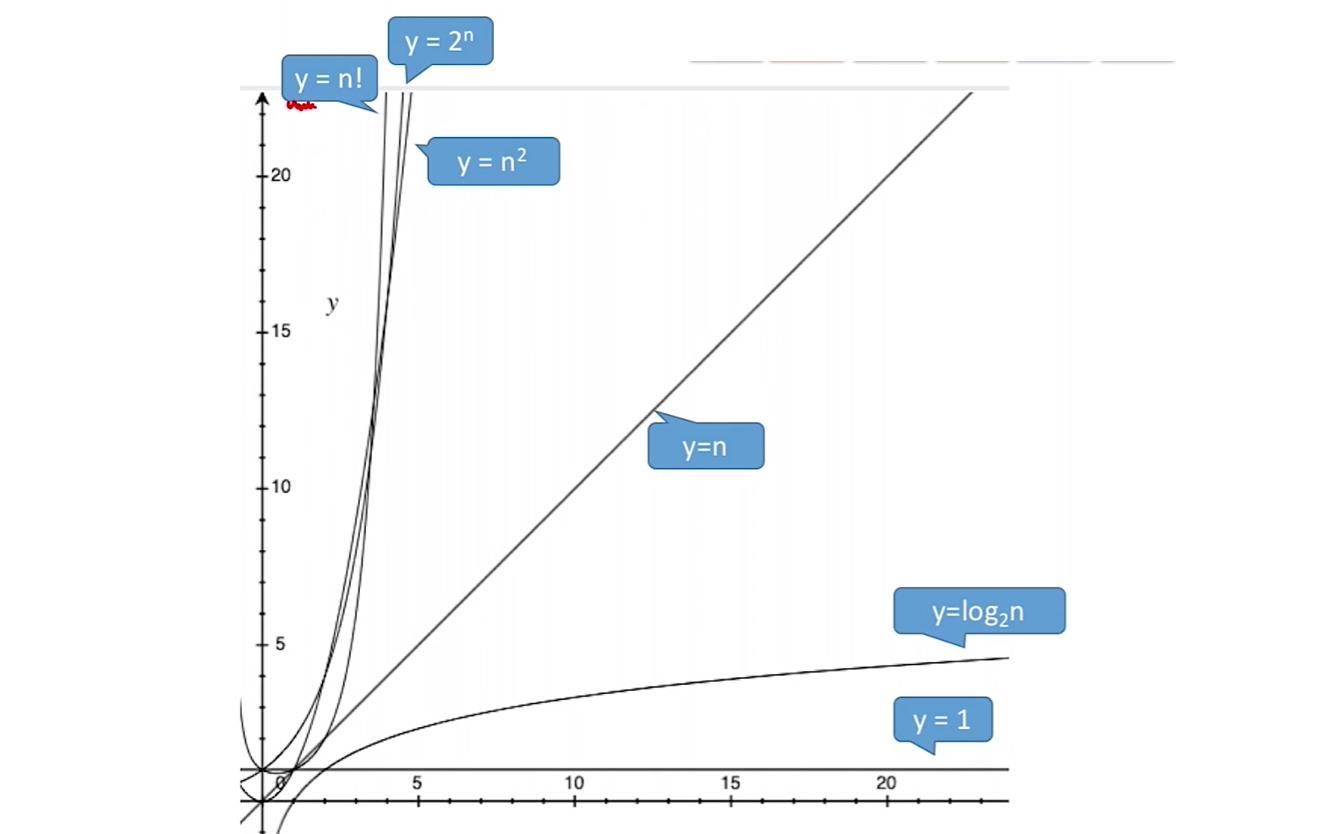
C：各阶分析

①：常数阶

高斯算法，很明显复杂度为 $O (1)$

int sum=0,n=100;//执行1次
sum=(1+n)*n/2;//执行1次
cout << sum//执行1次

但是如果是这样呢？

```c
int sum=0,n=100;//执行1次
sum=(1+n)*n/2;//执行1次
sum=(1+n)*n/2;//执行2次
sum=(1+n)*n/2;//执行3次
sum=(1+n)*n/2;//执行4次
sum=(1+n)*n/2;//执行5次
sum=(1+n)*n/2;//执行6次
sum=(1+n)*n/2;//执行7次
sum=(1+n)*n/2;//执行8次
sum=(1+n)*n/2;//执行9次
sum=(1+n)*n/2;//执行10次

cout << sum//执行1次

初学者很容易被其中置入的这些代码误导，事实上，无论n为多少；两段代码就是3和12的区别，仍然属于常数阶，也就是 $O (1)$ 同时对于分支结构，无论是真是假，执行的次数都是恒定的，所以单纯的分支结构（不包含在循环中），其时间复杂度也是 $O (1)$

②：线性阶

此时分析时间复杂度时，关键在于分析循环结构的运行情况

如下代码由于循环体中的代码执行n次，因此其时间复杂度为 $O (n)$

int i
for(i=0;i<n;i++)
{
	//时间复杂度为O(1)的程序步骤序列
}

③：对数阶

如下代码，由于循环中count乘以2之后，距离循环结束条件的n就更近了一步，也就是说现在在问你：有多少个2相乘后会大于n，那么自然得到答案是 $log_{2}n$ ，所以时间复杂度是 $O(log_{2}n)$

④：平方阶

如下例子，存在两个for循环，很明显其时间复杂度为 $O (m n)$ ，切当m=n时，时间复杂度为 $O(n^{2})$ ，所以 循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数

int i,j;
for(i =0;i<m;i++)
{
	for(j=0;j<n;j++)
	{
		//时间复杂度为O(1)的程序步骤序列	
	}
}

下面的这个例子呢？和明显这是一个等差数列，n+(n-1)+(n-2)+…+1= $\\frac{n^{2}}{2}$ + $\\frac{n}{2}$

(王道408考研操作系统)第二章进程管理-第二节3：调度算法详解2(RRHPF和MFQ)

(王道408考研数据结构)第二章线性表-第二节2：顺序表的操作

(王道408考研操作系统)第三章内存管理-第二节1：虚拟内存管理基本概念

(王道408考研操作系统)第三章内存管理-第二节2：页面置换算法2