数据结构二叉搜索树复习及创建求高度代码实现

Posted 2021-12-07 沉默的小宇宙

二叉搜索树（Binary Search Tree）的一些关键特点：

1）根节点 > 左孩子

2）根节点 < 右孩子

3）中序遍历是一个递增排序的数据

4）所有数据不能重复

typedef struct node
{
	int data;
	struct node *left;
	struct node *right;
}NODE_T,*PNODE_T;

typedef struct
{
	PNODE_T root;
}TREE_T,*PTREE_T;

/*
先序遍历：根->左->右
*/
void preorder(PNODE_T pNode)
{
	if(NULL != pNode)
	{
		printf(" %d",pNode->data);
		preorder(pNode->left);
		preorder(pNode->right);
	}
}

/*
中序遍历：左->根->右
*/
void inorder(PNODE_T pNode)
{
	if(NULL != pNode)
	{
		inorder(pNode->left);
		printf(" %d",pNode->data);
		inorder(pNode->right);
	}
}

/*
后序遍历：左->右->根
*/
void postorder(PNODE_T pNode)
{
	if(NULL != pNode)
	{
		postorder(pNode->left);
		postorder(pNode->right);
		printf(" %d",pNode->data);
	}
}

void insert(PTREE_T pTree,int value)
{
	PNODE_T pNewNode = malloc(sizeof(NODE_T));
	
	pNewNode->data = value;
	pNewNode->left = NULL;
	pNewNode->right = NULL;
	
	if(NULL == pTree->root)
	{
		pTree->root = pNewNode;
	}
	else
	{
		PNODE_T pNodeTmp = pTree->root;
		while(NULL != pNodeTmp)
		{
			if(value < pNodeTmp->data)	//左边
			{
				if(NULL == pNodeTmp->left)
				{
					pNodeTmp->left = pNewNode;
					break;
				}
				else
				{
					pNodeTmp = pNodeTmp->left;
				}
			}
			else						//右边
			{
				if(NULL == pNodeTmp->right)	//右边为空
				{
					pNodeTmp->right = pNewNode;
					break;
				}
				else
				{
					pNodeTmp = pNodeTmp->right;
				}
			}
		}
	}
}

/*求一棵树的高度*/
int get_height(PNODE_T pNode)
{
	if(NULL == pNode)
	{
		return 0;
	}
	else
	{
		int max=0;
		int left_height = get_height(pNode->left);
		int right_height = get_height(pNode->right);
		max = left_height > right_height ? left_height:right_height;
		return max+1;
	}
}
void test_binary_tree(void)
{
	int ary[7] = {6,3,8,2,5,1,7};
	TREE_T tree;
	tree.root = NULL;
	debug_set_level ( DBG_LEVEL_ALL );
	for(u8 i=0;i<7;i++)
	{
		insert(&tree,ary[i]);
	}

	DEBUG_INFO("preorder test !\\n");delay_ms(10);
	preorder(tree.root);	// 5 6 8 9 7 10
	printf("\\n");
	DEBUG_INFO("inorder test !\\n");delay_ms(10);
	inorder(tree.root);	// 8 6 9 5 10 7
	printf("\\n");
	DEBUG_INFO("postorder test !\\n");delay_ms(10);
	postorder(tree.root);	// 8 9 6 10 7 5
	printf("\\n");
	DEBUG_INFO(" end!\\n");
	
	DEBUG_INFO("the tree height is %d!\\n",get_height(tree.root));
	
	while(1)
	{
		
	}
}

测试数据：

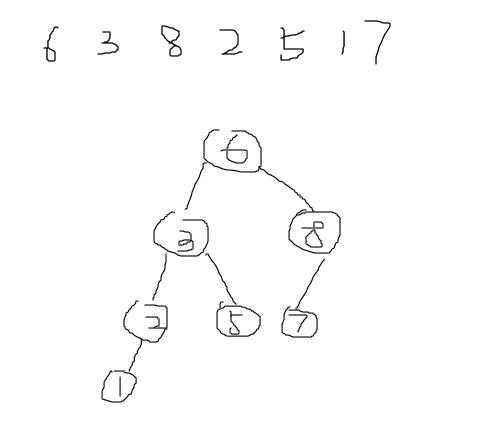
验证结果：

 

[INFO][bsp_test.c #466][@test_binary_tree]:preorder test !
 6 3 2 1 5 8 7
[INFO][bsp_test.c #469][@test_binary_tree]:inorder test !
 1 2 3 5 6 7 8
[INFO][bsp_test.c #472][@test_binary_tree]:postorder test !
 1 2 5 3 7 8 6
[INFO][bsp_test.c #475][@test_binary_tree]: end!
[INFO][bsp_test.c #477][@test_binary_tree]:the tree height is 4!

By Urien 2021/11/7