判断任意一点是否在矩形内(矩形可能与坐标轴有一定夹角)

Posted 2021-12-07 非晚非晚

1. 理论方法

1.1 点乘实现理论

• 问题

如何判断点$P$是否在被$P_1{P}_2{P}_3{P}_4$四个点围成的矩形框内？

• 方法

如果在矩形内：点$P$与矩形4个角的连线与任意轴形成的夹角都为锐角。可以用向量的点乘判断角度是否为锐角。具体方法如下图所示。

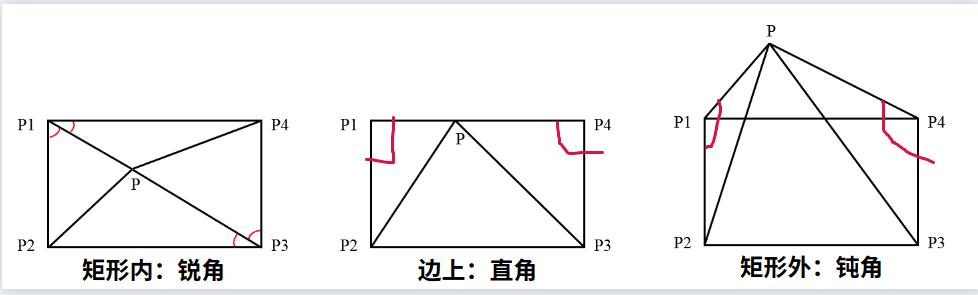
所以可以通过下列公式判断：

$$点P位于矩形框内\iff \{\begin{array}{l}\angle P{P}_1{P}_4<90\\ \angle P{P}_1{P}_2<90\\ \angle P{P}_3{P}_4<90\\ \angle P{P}_3{P}_2<90\end{array}\iff \{\begin{array}{l}\stackrel{\rightharpoonup }{P_{1}P}\ast \stackrel{\rightharpoonup }{P_1{P}_4}>0\\ \stackrel{\rightharpoonup }{P_{1}P}\ast \stackrel{\rightharpoonup }{P_1{P}_2}>0\\ \stackrel{\rightharpoonup }{P_{3}P}\ast \stackrel{\rightharpoonup }{P_3{P}_4}>0\\ \stackrel{\rightharpoonup }{P_{3}P}\ast \stackrel{\rightharpoonup }{P_3{P}_2}>0\end{array}$$

1.2 叉乘实现理论

只需要判断点$P$是否在上下两条边和左右两条边之间就可以，判断一个点是否在两条线段之间夹着，可以使用叉乘来判断，当$(P_1{P}_2\times P_{1}P)\ast (P_3{P}_4\times P_{3}P)>=0$时，说明点$P$在$P_1{P}_2$与$P_3{P}_4$的中间。同理判断两边即可。所以点$P$在矩形内的条件为：
$$(P_1{P}_2\times P_{1}P)\ast (P_3{P}_4\times P_{3}P)>=0and(P_2{P}_3\times P_{2}P)\ast (P_4{P}_1\times P_{4}P)>=0$$

2. 代码实现

2.1 点乘方法实现

#include<iostream>
struct MPoint
{
    double x;
    double y;
};
struct RectPoint
{
    MPoint p1;
    MPoint p2;
    MPoint p3;
    MPoint p4;
};
bool isPointInRect(MPoint p, RectPoint rect)
{
    if ((rect.p1.x - p.x) * (rect.p1.x - rect.p4.x) + (rect以上是关于判断任意一点是否在矩形内(矩形可能与坐标轴有一定夹角)的主要内容，如果未能解决你的问题，请参考以下文章
 
 java知道四个点坐标,怎么判断一个点是否在这个矩形区域内（矩形可能是斜着放的，有一定的斜度）
 平面坐标系中 如何判断某一点在一矩形区域内？
 用java实现：一个斜向矩形，已知4个点，判断任意一点是不是在区域内？
 判断点是否在一个矩形内
 平面中判断线段与矩形是否相交
 如何判断一个点在一个矩形里边，一直点和矩形的坐标点位置。