用数学方式打开Facebook新Logo，真的和视频号Logo来自同一方程

Posted 2021-12-07 QbitAl

梦晨 发自 凹非寺
量子位 报道 | 公众号 QbitAI

Facebook改名Meta，也换了新Logo。

国内网友吐槽这Logo长得太像微信视频号，外国网友则直接上手P图来了场恶搞的狂欢。

热度来得快去得也快。

就在大家快玩腻的时候，却有人悄悄发现这Logo背后其实暗藏玄机。

有一个神奇的方程：x=Asin(at+δ), y=Bsin(bt), 0≤t≤2π。

看不懂也没关系，只要赋上合适的值，剩下的都交给画图软件就行了。

软件不支持δ(delta)符号，换成了d

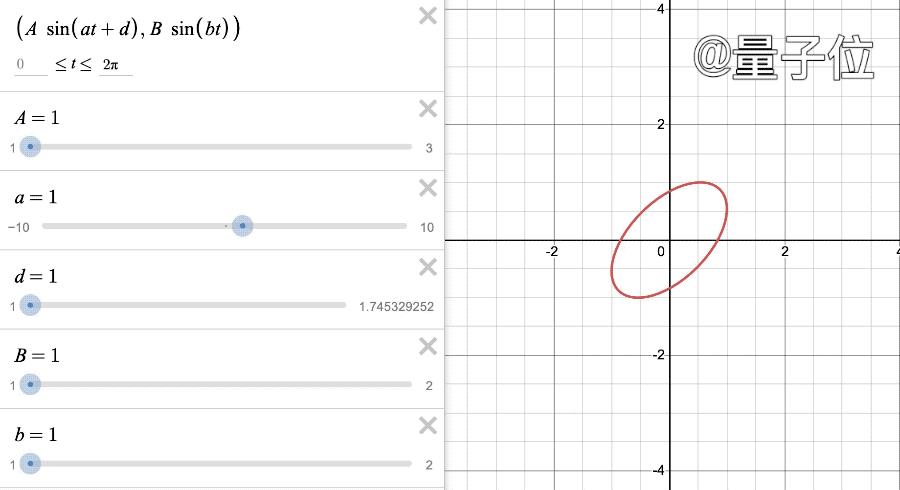
把参数稍稍一变，就成了微信视频号。

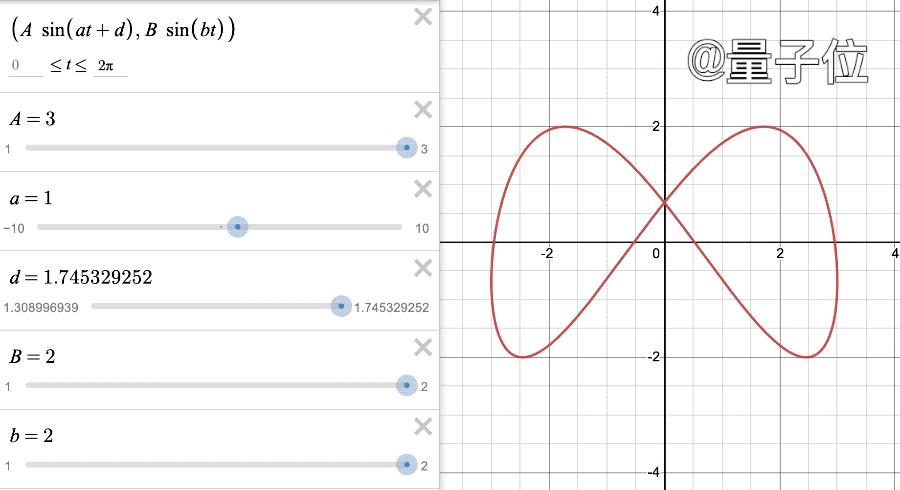
怪不得大家会觉得两个logo很像，原来背后还有这样的联系。

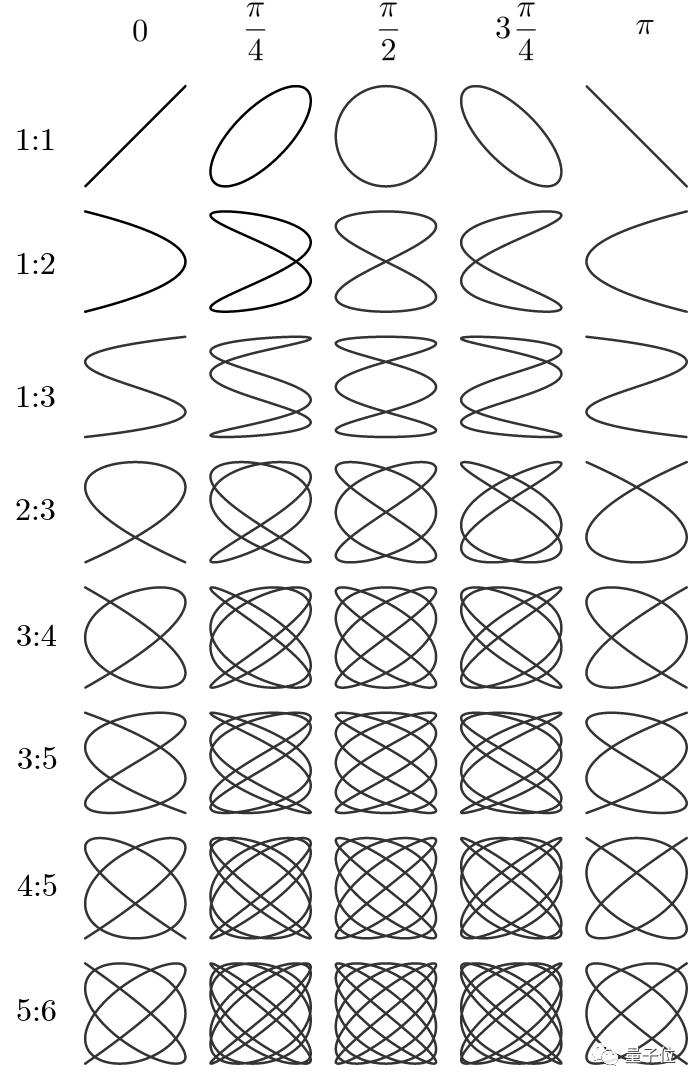
在数学上，这样的图形叫做李萨如曲线 （Lissajous Curve），严格的定义是“两个沿着互相垂直方向的正弦振动合成的轨迹。”

d这个参数取值看起来很怪，其实是5π/9和5π/12。

从三维空间看Meta

Facebook，啊不是，Meta公司开发布会的时候，宣传视频里有这么一段三维动画：

李萨如图形也可以再加上一个z轴，变成一条三维曲线。

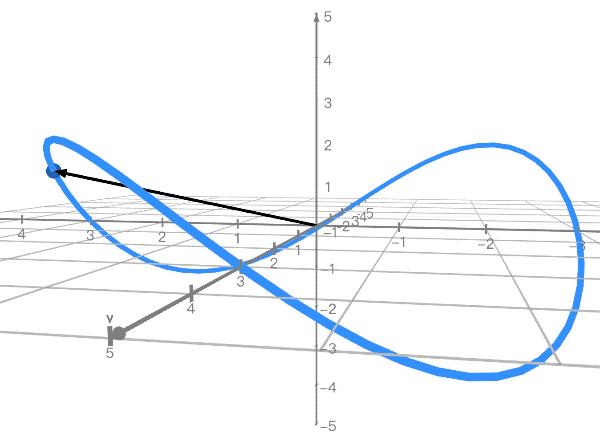
如果把2D的李萨如曲线看作是3D曲线在平面的投影，那么参数δ就是控制我们观察的角度。

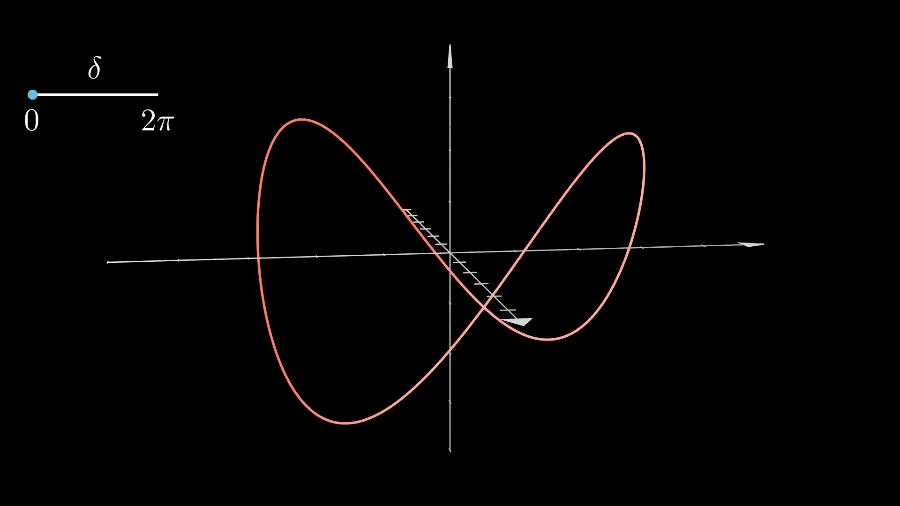
结合这段动画，原来这里Logo的变化是在三维空间中做旋转。

这时再回过头去看Meta公司宣传文案中的这段话：

在2d和3d之间无缝切换的动态符号，为从不同的视角和交互方式体验而设计。可以代表Meta的M，有时也代表无限，象征元宇宙中的无限视野。

似乎有那么点元宇宙的味了。

李萨如曲线本来是干嘛的？

朱尔斯·安东尼·李萨如 （Jules Antoine Lissajous）本人是一位19世纪的法国物理学家，研究的是如何用图形来表示看不见的声音。

他做出一套装置，先把小镜子贴在音叉的末端。

然后用光线照射第一个音叉上的小镜子，反射到第二个音叉，再反射到一个放大镜。

如果两次反射的光线相互垂直，音叉震动的频率成特定比例，就可以观察到各种各样的李萨如曲线了。

李萨如推广这套设备用于乐器校准，这样就不是非得找耳朵好使的人来判断音高准不准了。

结果超出意料的成功，1859年法国政府邀请他参加工作组，用这套设备制定了国家音高标准，把435Hz定为标准音。

后来1939年伦敦重新把标准音定义为440Hz，成为通用的“第一国际音高”沿用到今天。法国的435Hz现在被称作“第二国际音高”。

李萨如这项研究是借鉴了之前一位纳撒尼尔·鲍迪奇的想法，所以这种曲线也可以叫做鲍迪奇曲线，也有叫李萨如图形、鲍迪奇图形的，再加上李萨如的不同译法，总之名字不少。

除了校准声音之外，李萨如那个时代也有人对画出来的图形更感兴趣。

以格拉斯哥大学一位教授Hugh Blackburn为代表的一些人用发明了一套机械的谐波记录仪（Harmonograph）。

这种装置夹上一根笔就能画出纷繁复杂的图案，怪好看的，也受到了艺术圈的关注。

艺术圈对李萨如曲线的兴趣延续到今天，很多机构和品牌的Logo设计中都能找到李萨如曲线的身影。

比如……中央电视台的旧版台标。

过去电视台经常用到的示波器就能输入两个正弦波产生李萨如曲线，难道设计灵感是从这来的？

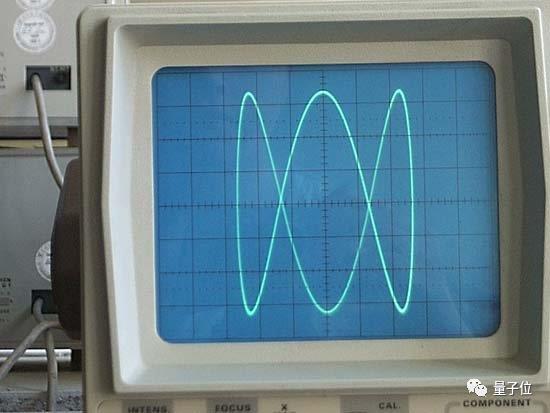
还有很多大学的实验室用了这种曲线，就不一一列举了。

近几年的有迪士尼推出的在线观影平台Movies Anywhere。

然后就是最近的Meta了。

谁发现了Meta的秘密

Nathaniel Budijono在自己的GitHub博客解释了Meta的Logo与李萨如曲线的关系。

这位小哥目前在明尼苏达大学学习计算机和数学，经常在GitHub上发布一些开源项目和数学科普。

他画图使用的工具是Desmos和Manim。

感兴趣的话可以点击文章最后的阅读原文，试试Desmos在线版。

方程已经写好，只需动手调调参数，看你能不能找出还有哪些Logo也用了李萨如曲线。

参考链接：
[1]https://nathanielbd.github.io/posts/what-is-the-meta-logo/
[2]https://design.facebook.com/stories/designing-our-new-company-brand-meta/
[3]https://www.historyofinformation.com/detail.php?id=3263
[4]https://www.encyclopedia.com/science/dictionaries-thesauruses-pictures-and-press-releases/lissajous-jules-antoine