盲签名 blind signature

Posted 2021-12-07 mutourend

1. 引言

前序博客有：

• Coconut：可selective disclosure credentials的门限发行签名机制
• ECDSA VS Schnorr signature VS BLS signature
• 密码学算法——RSA

盲签名（blind signature）为：
一种数字签名的方式，在消息内容被签名之前，对于签名者来说消息内容是不可见的。

类比例子：对文件签名就是通过在信封里放一张复写纸，签名者在信封上签名时，他的签名便透过复写纸签到文件上。

盲签名除具有普通数字签名特征之外，还额外具有如下特征：

• 1）签名者对其所签署的消息是不可见的，即签名者不知道其所签署消息的具体内容。
• 2）签名消息不可追踪，即当签名消息被公开时，签名者无法知道其哪次签署了该消息。

盲签名的基本流程为：

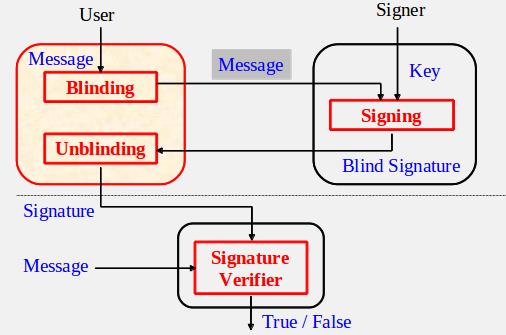
实现盲签名的方案主要有：

• 基于RSA的盲签名
• 基于BLS-signature的盲签名

2. 基于RSA的盲签名

基本背景参看：

• 密码学算法——RSA

$(e,n)$为公钥，$d$为私钥，其中$ed\equiv (p-1)(q-1)\mathrm{m}\mathrm{o}\mathrm{d}n$。$m\in [0,n-1]$为待签名消息。
为让签名者不知道所签名的消息$m$，需引入一个参数$r$（仅用户可知），使得$gcd(r,n)=1$。
基于RSA的盲签名流程为：

• 1）用户blinding消息：$m^{\prime }\equiv m{r}^e(\mathrm{m}\mathrm{o}\mathrm{d}n)$
• 2）签名者对已盲化的消息进行签名：$s^{\prime }\equiv (m^{\prime }{)}^d(\mathrm{m}\mathrm{o}\mathrm{d}n)$
• 3）用户收到签名后进行unblinding操作：$s\equiv s^{\prime }\cdot r^{-1}(\mathrm{m}\mathrm{o}\mathrm{d}n)$
• 4）任何人，采用公钥$(e,n)$，可对$m$和$s$验签：$s^e\equiv m^{ed}(\mathrm{m}\mathrm{o}\mathrm{d}n)=m(\mathrm{m}\mathrm{o}\mathrm{d}n)$。

基于RSA的盲签名方案有效的原因是：
$r^{ed}\equiv r(\mathrm{m}\mathrm{o}\mathrm{d}n)$
$s\equiv s^{\prime }\cdot r^{-1}\equiv (m^{\prime }{)}^d{r}^{-1}\equiv m^d{r}^{ed}{r}^{-1}\equiv m^{d}r{r}^{-1}\equiv m^d(\mathrm{m}\mathrm{o}\mathrm{d}n)$

基于RSA的盲签名存在的一个问题是：
通过RSA blinding attack，可能可利用盲签名将一个消息解密为另一消息。
因为盲签的过程等价为使用签名者使用私钥$d$解密的过程，攻击者可提供已 经签名者公钥加密的消息$m^{\prime }=m^e$，具体流程为：

• 1）攻击者blinding消息：$m^{\prime \prime }\equiv m^{\prime }{r}^e(\mathrm{m}\mathrm{o}\mathrm{d}n)\equiv (m^e(\mathrm{m}\mathrm{o}\mathrm{d}n)\cdot r^e)(\mathrm{m}\mathrm{o}\mathrm{d}n)=(mr{)}^e(\mathrm{m}\mathrm{o}\mathrm{d}n)$
• 2）签名者签名：$s^{\prime }\equiv (m^{\prime \prime }{)}^d(\mathrm{m}\mathrm{o}\mathrm{d}n)\equiv ((mr{)}^e(\mathrm{m}\mathrm{o}\mathrm{d}n){)}^d(\mathrm{m}\mathrm{o}\mathrm{d}n)\equiv (mr{)}^{ed}(\mathrm{m}\mathrm{o}\mathrm{d}n)\equiv m\cdot r(\mathrm{m}\mathrm{o}\mathrm{d}n)$
• 3）攻击者unblinding：$s\equiv s^{\prime }\cdot r^{-1}(\mathrm{m}\mathrm{o}\mathrm{d}n)\equiv m(\mathrm{m}\mathrm{o}\mathrm{d}n)\ne m^{\prime }$。本来发送给签名者的加密消息$m$应只有签名者通过私钥获知，而此时攻击者借助盲签名，获知了相应的加密消息$m$。

3. 基于BLS-signature的盲签名

基本背景参看：

• ECDSA VS Schnorr signature VS BLS signature
  

参考资料

[1] Which blind signature schemes exist, and how do they compare?
[2] 维基百科 Blind signature
[3] 盲签名 blind signature 简介