学习数据结构笔记====＞不同的排序算法(Sort Algorithm)[冒泡,选择,插入,快速,希尔,基数,归并]
Posted 小智RE0
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了学习数据结构笔记====＞不同的排序算法(Sort Algorithm)[冒泡,选择,插入,快速,希尔,基数,归并]相关的知识，希望对你有一定的参考价值。
B站学习传送门–>尚硅谷Java数据结构与java算法（Java数据结构与算法）
写在前面
数组结构可视化在线网站地址 ===>数据结构可视化在线
排序算法: 把一组数据，依指定顺序进行排列的过程.
ml
1.时间复杂度概述
时间频度
时间频度(T(n)) 算法中语句的执行次数
案例
时间频度为 (n+1);
这里的n就是100;
加1是因为最后在循环时还要再判断一次;
public class Demo01 {
public static void main(String[] args) {
int total = 0;
int end = 100;
for (int i = 1; i <= end; i++) {
total +=i;
}
System.out.println(total);//5050
}
}
但是若直接简化写为;
时间频度就变成 1 ;因为仅执行一次
public class Demo01 {
public static void main(String[] args) {
int total = 0;
int end = 100;
total =(end +1 )* end/2;
System.out.println(total);//5050
}
}
实际上,常数项可以忽略
低阶的次数项也可以忽略
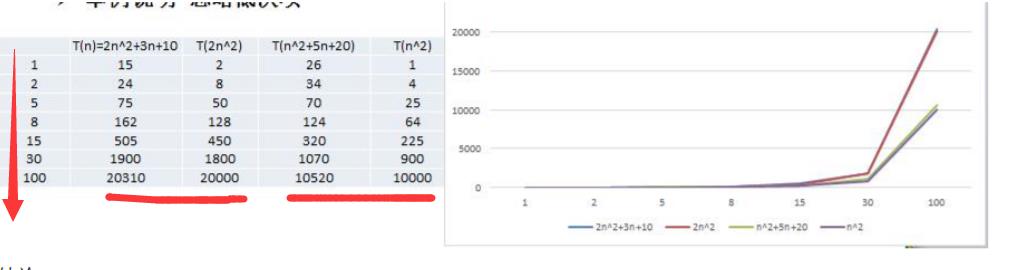
在同等次方的条件下,和次方项前面的系数有关系;去掉系数后;这个就接近了
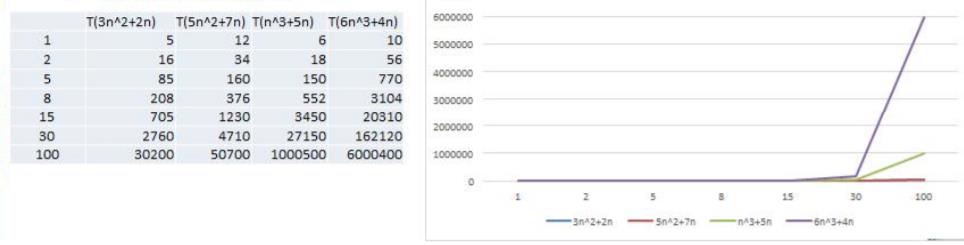
时间复杂度
在计算机科学中，时间复杂性，又称时间复杂度，算法的时间复杂度是一个函数，它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述，不包括这个函数的低阶项和首项系数。使用这种方式时，时间复杂度可被称为是渐近的，亦即考察输入值大小趋近无穷时的情况。
一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n),使得当n趋近于无穷大时，T（n)/f (n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n)) 为算法的渐进时间复杂度，简称时间复杂度。
时间频度不同,时间复杂度可能相同
例: T(n) = n² + 6n+2 与 T(n) = 2n² + 5n+2
时间复杂度都可写为 O(n²)
Ο(1)＜Ο(log₂n)＜Ο(n)＜Ο(nlog₂n)＜Ο(n²)＜Ο(n³)＜ Ο(n^k) ＜Ο(2ⁿ)
时间复杂度增大,效率变低
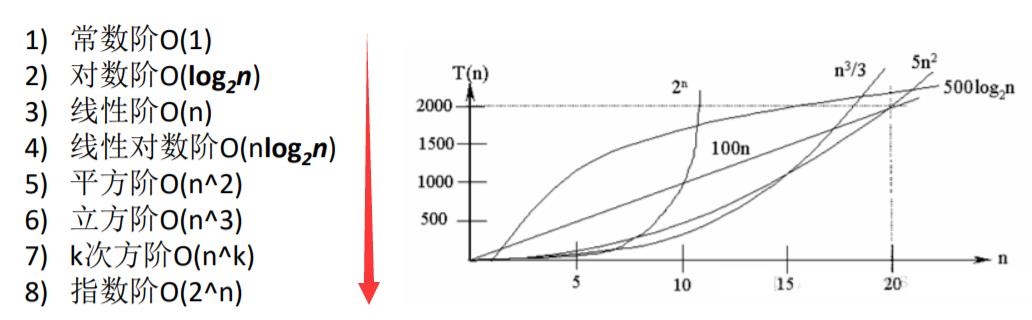
常数阶 Ο(1):
只要里面没有循环之类的复杂运算,代码再多也都是O(1)常数阶;
不会因为某个变量的增加而增加消耗的时间
对数阶: Ο(log₂n)
案例:比如说要计算下面这个循环次数;
在while循环内;每次都给 i *2 ;条件是i<1024;
1024 = 2^10; 即 n = 2^10; 那么对应的就是 log₂n = 10; 执行的次数为10次;
即时间复杂度为对数阶O(log₂n);
当然,这个根据实际情况会发生改变; 若 在循环中变为i = i * 5;那么时间复杂度也就是O(log5n)
public class Demo02 {
public static void main(String[] args) {
int i = 1;
int n =1024;
//num:用来计数
int num = 0;
while (i<n){
i = i * 2 ;
num++;
}
System.out.println("执行次数->"+num); //执行次数->10
}
}
线性阶:O(n)
单层循环的话,按照循环的规模来决定; 时间复杂度就是O(n)
案例;它的执行次数为 T(n) = n +1 ;
忽略掉常数项 ; 时间复杂度其实就是O(n);
在本案例中循环的规模n=10;那么它时间复杂度为O(10);
当n变为20时,它也就是O(20);总的来说,时间复杂度就是线性阶的O(n)
public class Demo03 {
public static void main(String[] args) {
int w =0;
int num = 0;
int n =10;
for (int i = 0; i <= n ; i++) {
w = num;
num ++;
}
System.out.println(w); // 10
System.out.println("执行次数->"+num);//执行次数->11
}
}
线性对数阶Ο(nlog₂n)
实际上就是让时间复杂度为O(log₂n)的再循环n次
案例;这里执行次数就是 T(n) = (n+1) * (log₂n)
public class Demo04 {
public static void main(String[] args) {
int n =1024;
int i ;
//num:用来计数
int num = 0;
for (int m = 0; m <= n; m++) {
i =1;
while (i<n){
i = i * 2 ;
num++;
}
}
System.out.println("执行次数->"+num); //执行次数->10250 (1024+1) * 10
}
}
平方阶Ο(n²)
实际就是把时间复杂度为O(n)的再嵌套一层循环;即双层循环;也可写作O( m* n)
案例
public class Demo05 {
public static void main(String[] args) {
int w =0;
int num = 0;
int m =10;
int n =10;
for (int i = 1; i <= m ; i++) {
for (int j = 1; j <= n; j++) {
w = num;
num ++;
}
}
System.out.println(w); // 99
System.out.println("执行次数->"+num);//执行次数->100
}
}
平均&最差时间复杂度
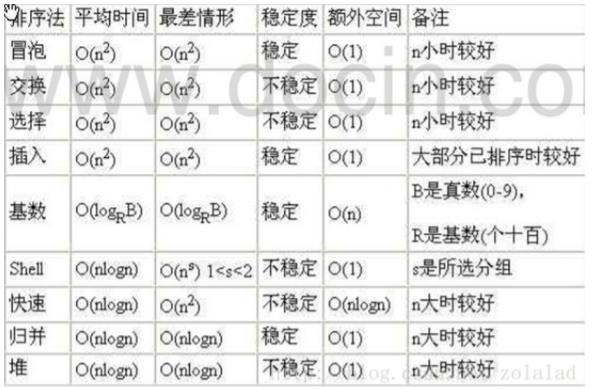
2.冒泡排序
按照提前设定的规则 (由小到大 / 由大到小) ;比较前后两个相邻元素的大小;若逆序了,就发生交换;
例如需要完成由小到大冒泡排序:29,10,14,37,14,3
图示:–>
初始的理解过程
总共经过数组的(长度-1)次大的交换过程;即 5 次;
其实每次大的排序结束后就有一个最大的值固定下来了;所以循环次数会比上一次的少一次
(1)
10 -> 29 -> 14 -> 37 -> 14 -> 3
10 -> 14 -> 29 -> 37 -> 14 -> 3
10 -> 14 -> 29 -> 37 -> 14 -> 3
10 -> 14 -> 29 -> 14 -> 37 -> 3
10 -> 14 -> 29 -> 14 -> 3 -> 37
(2)
10 -> 14 -> 29 -> 14 -> 3 -> 37
10 -> 14 -> 29 -> 14 -> 3 -> 37
10 -> 14 -> 14 -> 29 -> 3 -> 37
10 -> 14 -> 14 -> 3 -> 29 -> 37
(3)
10 -> 14 -> 14 -> 3 -> 29 -> 37
10 -> 14 -> 14 -> 3 -> 29 -> 37
10 -> 14 -> 3 -> 14 -> 29 -> 37
(4)
10 -> 14 -> 3 -> 14 -> 29 -> 37
10 -> 3 -> 14 -> 14 -> 29 -> 37
(5)
3 -> 10 -> 14 -> 14 -> 29 -> 37
分步骤写法;
这里分步骤展示排序过程
public class BubbleSortTest2 {
public static void main(String[] args) {
//需要排序的数组
int[] array = {29,10,14,37,14,3};
//临时变量,用于前后交换时临时存储;
int temp = 0;
//1.第一次排序;
for (int i = 0; i < array.length - 1; i++) {
if(array[i] > array[i+1]){
temp = array[i];
array[i] = array[i+1];
array[i+1] =temp;
}
}
System.out.println("第一次排序后-->"+ Arrays.toString(array));
//第一次排序后-->[10, 14, 29, 14, 3, 37]
//2.第二次排序;
for (int i = 0; i < array.length - 1 - 1; i++) {
if(array[i] > array[i+1]){
temp = array[i];
array[i] = array[i+1];
array[i+1] =temp;
}
}
System.out.println("第二次排序后-->"+ Arrays.toString(array));
//第二次排序后-->[10, 14, 14, 3, 29, 37]
//3.第三次排序
for (int i = 0; i < array.length - 1 - 1 - 1; i++) {
if(array[i] > array[i+1]){
temp = array[i];
array[i] = array[i+1];
array[i+1] =temp;
}
}
System.out.println("第三次排序后-->"+ Arrays.toString(array));
//第三次排序后-->[10, 14, 3, 14, 29, 37]
//4.第四次排序;
for (int i = 0; i < array.length - 1 - 1 -1; i++) {
if(array[i] > array[i+1]){
temp = array[i];
array[i] = array[i+1];
array[i+1] =temp;
}
}
System.out.println("第四次排序后-->"+ Arrays.toString(array));
//第四次排序后-->[10, 3, 14, 14, 29, 37]
//5.第五次排序;
for (int i = 0; i < array.length - 1 - 1 -1; i++) {
if(array[i] > array[i+1]){
temp = array[i];
array[i] = array[i+1];
array[i+1] =temp;
}
}
System.out.println("第五次排序后-->"+ Arrays.toString(array));
//第五次排序后-->[3, 10, 14, 14, 29, 37]
}
}
综合写法
public class BubbleSortTest {
public static void main(String[] args) {
//需要排序的数组
int[] array = {29,10,14,37,14,3};
//调用方法; 完成由大到小排序
int[] sortArray = BubbleSort(array);
System.out.println("冒泡排序结果-->"+Arrays.toString(sortArray));
//冒泡排序结果-->[3, 10, 14, 14, 29, 37]
}
public static int[] BubbleSort(int[] array){
for (int i = 0; i <array.length -1; i++) {
for (int j = 0; j < array.length - i - 1; j++) {
//后一个和之前的交换;
if(array[j] > array[j+1]){
int temp = array[j];
array[j] = array[j+1];
array[j+1] = temp;
}
}
System.out.println("第"+(i+1)+"次排序后-->"+Arrays.toString(array));
}
return array;
}
}
运行结果
第1次排序后-->[10, 14, 29, 14, 3, 37]
第2次排序后-->[10, 14, 14, 3, 29, 37]
第3次排序后-->[10, 14, 3, 14, 29, 37]
第4次排序后-->[10, 3, 14, 14, 29, 37]
第5次排序后-->[3, 10, 14, 14, 29, 37]
冒泡排序结果-->[3, 10, 14, 14, 29, 37]
稍微优化一下
如果说,我这个数组比较特殊;
例如:3,2,14,37,14,3
看看它的执行步骤;会发现其实第三次它就排序完成了;但还进行了后面的无意义排序;
第1次排序后-->[2, 3, 14, 14, 3, 37]
第2次排序后-->[2, 3, 14, 3, 14, 37]
第3次排序后-->[2, 3, 3, 14, 14, 37]
第4次排序后-->[2, 3, 3, 14, 14, 37]
第5次排序后-->[2, 3, 3, 14, 14, 37]
冒泡排序结果-->[2, 3, 3, 14, 14, 37]
那么,就对之前的冒泡排序优化一下;
在执行时加入标志位的判断;
public class BubbleSortTest3 {
public static void main(String[] args) {
//需要排序的数组
int[] array = {3,2,14,37,14,3};
//调用方法; 完成由大到小排序
int[] sortArray = BubbleSort(array);
System.out.println("冒泡排序结果-->"+Arrays.toString(sortArray));
}
public static int[] BubbleSort(int[] array){
//定义标志位;
boolean flag =false;
for (int i = 0; i <array.length -1; i++) {
for (int j = 0; j < array.length - i - 1; j++) {
//后一个和之前的交换;
if(array[j] > array[j+1]){
flag = true;
int temp = array[j];
array[j] = array[j+1];
array[j+1] = temp;
}
}
//对标志位判断后再决定是否继续循环;
if(flag){
//重置标志位;
flag = false;
}else {
//表示没发生交换;跳过本次循环;
break;
}
System.out.println("第"+(i+1)+"次排序后-->"+Arrays.toString(array));
}
return array;
}
}
看看执行过程
第1次排序后-->[2, 3, 14, 14, 3, 37]
第2次排序后-->[2, 3, 14, 3, 14, 37]
第3次排序后-->[2, 3, 3, 14, 14, 37]
冒泡排序结果-->[2, 3, 3, 14, 14, 37]
3.简单选择排序
比如说要定义由小到大的排序;
首先假设数组的第一个数是最小的数;去依次和后面的数进行比较,直到找到一个比它小的,然后将那个数标记为最小的数,接着继续依次比较;直到数组遍历结束;将带有标
以上是关于学习数据结构笔记====＞不同的排序算法(Sort Algorithm)[冒泡,选择,插入,快速,希尔,基数,归并]的主要内容，如果未能解决你的问题，请参考以下文章
python 学习笔记 -- 数据结构与算法 冒泡排序 Bubble sort
python 学习笔记 -- 数据结构与算法 插入排序 Insertion Sort
python 学习笔记 -- 数据结构与算法 归并排序 Merge Sort
python 学习笔记 -- 数据结构与算法 快速排序 Quick Sort