归并排序与快速排序背后的秘密

Posted 2021-12-07 dog250

排序问题一直都是各类考试和面试的热门问题，在读了《算法之美》第三章后，就发觉其实它在各个场合都很热门。其实我们一直在不断地排序，无论我们做什么。

说回具体的考试面试中的排序，很多人都能用各种语言写出各种排序算法，但很少有人会去思考这些算法步骤背后的秘密，那么本文来抛块砖，说说归并排序和快速排序。

到处都讲归并排序采用分治方法，所以效率比冒泡排序高：

将一个大问题分解成一些小问题，分而治之，各个击破…

但这些诠释都缺了关键点，即 效率必须随规模非线性增加的场景，分治才有意义，如果是线性系统，比如计数，分时调度，分治反而增加额外开销。

只要记住，基于比较的排序效率随着规模下凸增加，就足以理解分治方法了。这很容易理解，每次比较涉及两个数而不是一个，这意味着比较的次数比参与比较的数字规模更大。

把规模缩小一倍，排序效率便不止提升一倍，这是分治策略的基础。排序两个子数组(相当于降维)然后再合并的效率一定比直接排序一个大数组效率高，在此基础之上再看归并排序的时间复杂度。

设待排序数组大小为$n$，使用冒泡排序算法，需要比较的次数为：

$T(n)=(n-1)+(n-2)+...+1=\frac{n(n-1)}{2}$

按照时间复杂度的定义忽略小阶项，$T(n)$可以等价为$n^2$。

现在将数组均拆成两半，每一半分别冒泡排序，然后合并两个有序子数组，设$T_i$为将数组均拆成$i$个子数组时的排序时间复杂度度量，则：

$T_2(n)=2(\frac{n}{2}{)}^2+n$

具体采用什么算法排序子数组无所谓，只是为了演示经过$\log n$次均拆之后，子数组将仅剩下一个元素，整个归并排序只需要$\log n$层的子数组合并即可，而每层若干合并的总比较次数为$n$。

继续均拆，随着子数组变小，排序涉及的比较次数指数递减。

将大小为$i$的子数组逐级合并为大小为$2i$的子数组，每次合并操作涉及的操作次数固定为$n$，对于不同的$i$，总比较次数分别为：

$T_4(n)=4(\frac{n}{4}{)}^2+2n$

$T_8(n)=8(\frac{n}{8}{)}^2+3n$
…

可以期望，子数组大小肯定会递减到1，合并两个大小为1的子数组仅需一次比较，此时：

$T_n(n)=n(\frac{n}{n}{)}^2+n{\log }_{2}n=n{\log }_{2}n+n$

这就是归并排序的时间复杂度$O(n{\log }_{2}n)$。从这个过程发现无论最好，最坏，平均，归并排序的时间复杂度不变。

这是一个非常清晰的过程，但并没有回答一个核心问题，与$O(n^2)$的冒泡排序相比，归并排序到底省掉了哪些比较，从而让时间复杂度减少到$O(\log n)$？

看一下合并两个已排序数组的过程，请看下图：

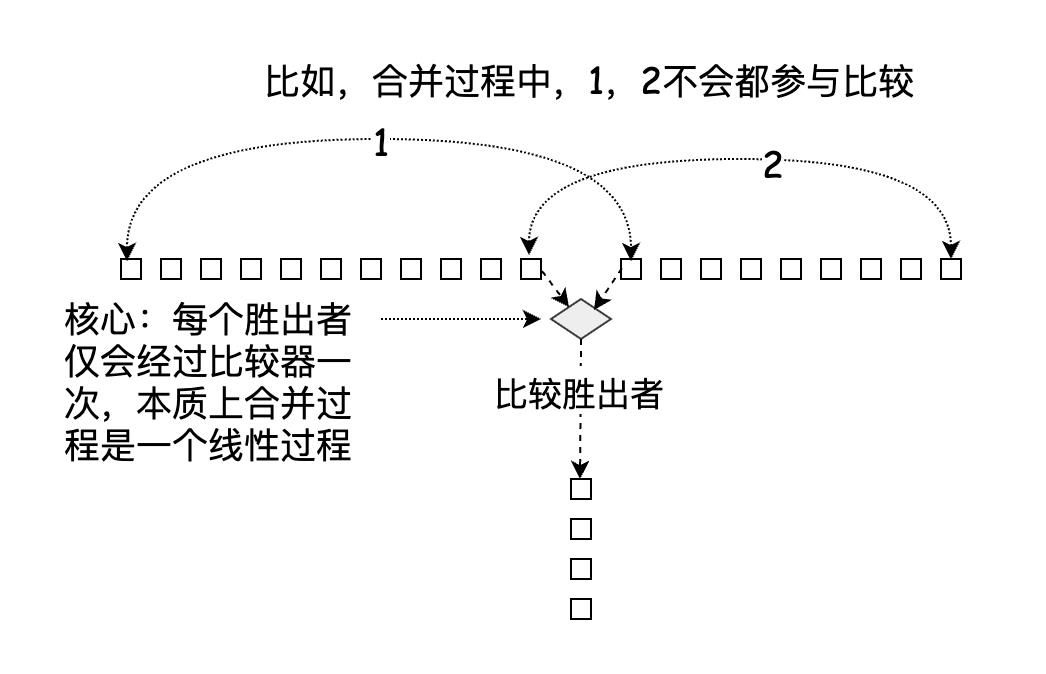
两个有序子数组中两组数字，其中一个的头和另一个的尾，在一次合并中不会同时参与比较，减少的比较操作正是来源于此，经过不断分治，归并排序实际上就是一个递归合并的过程。

若仅仅考虑时间复杂度，归并排序可以证明是最高效的排序算法。$O(n\log n)$是比较排序算法绕不过的极限，而这很容易证明。

$n$个数字有$n!$种序列，升序(或者降序)是其中一种。$n$个数字中两数经过一次比较可确定两数的相对位置，那么就剩下$\frac{n!}{2}$种序列，在$\frac{n!}{2}$种序列中，再比较一次，就会剩下$\frac{n!}{4}$种序列，以此类推，现在问，至少比较多少次能只剩下1种序列，设比较$x$次可达，那么：

$2^x\ge n!$

两边取对数，解$x$，即：

$x\ge {\log }_{2}n!$

不等号右边用斯特林公式近似，得到比较排序的时间复杂度极限$O(n\log n)$，而归并排序就是比较排序的一种，它的最差情况都能达到$O(n\log n)$，这无疑是最棒的算法。

遗憾的是，它的空间复杂度为$O(n)$，在实际实现中，随着$n$的增加，排序操作需要大量的内存，这非常不利于cache亲和，而快速排序的原地排序优化可以避免空间问题，这就是快速排序胜出的原因。

那么快速排序为什么可以胜任？它的时间复杂度表现如何呢？

很著名的一篇文章：
数学之美番外篇：快排为什么那样快
我觉得小题大做了，没那么复杂，快速排序核心就是随机，如果每次都能抓到剩余子数组的中位数，每次都是均拆，考虑到每拆到一层$i$，该层比较总和为$n-1-i$，总的操作次数是可以算出来的：

$T=\sum _{i=0}^{\log n}(n-1-i)$

在最好的情况下，快速排序和归并排序时间复杂度均一致，均为$O(n\log n)$。

但每次都抓住中位数几乎不可能，$n$个数选一个，概率均为$\frac{1}{n}$，所有子数组均能选中中位数概率可想而知。

无论是否抓到了中位数，快速排序每一步总是可以将子数组分成两个部分，相比$O(n^2)$的冒泡排序，快速排序减少比较次数从而降低时间复杂度的秘密在于，在某层被拆开的两部分之间，直到排序结束，均不会发生任何比较。

既然最好情况几乎不可达，最差时间复杂度又是不可接受的$O(n^2)$，问题是，平均情况下，距离最好情况，差多少呢？如果平均情况接近最好情况，也不错。

快速排序的平均情况显然也是$O(n\log n)$，若非如此，也就没有本文，问题是不光要把它推导出来，还要能直观地描绘出来。

平均情况体现在所有排序可能性最接近所有可能性平均数的地方，下图展示了最坏情况到最好情况的单调过渡：

退化成链表的二叉树高度为$h=n$，它逐渐变矮，直到满二叉树最矮$h=\log n$，这个过程中，$h$越小，可以构造的二叉树越多，可能性分布越密集。而每一棵二叉树都表示一种可能的快速排序，所有可能的平均数位置必然接近密度最大处，显然$h_{avg}$会很小：

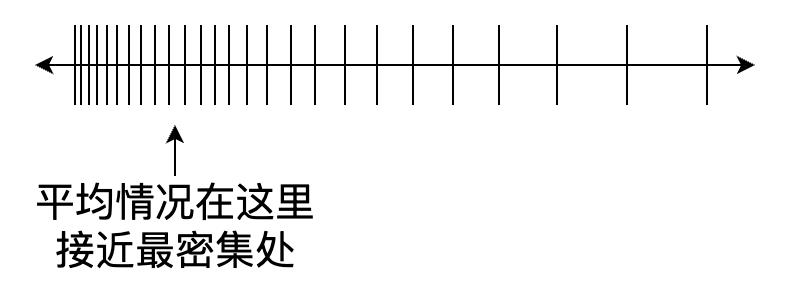
有了直观的感受，推导出来的平均时间复杂度就容易理解了。来自wiki，设$T(n)$为排序$n$个数所需的操作：

T ( n ) = 1 n ∑ i = 0 n − 1 ( T ( i ) + T ( n − i − 1 ) ) + ( n − 1 ) = 1.39 n log ⁡ n T(n)=\\dfrac{1}{n}\\sum\\limits_{i=0}^{n-1}(T(i)+T(n-i-1))+(n-1)=1.39n\\log n

以上是关于归并排序与快速排序背后的秘密的主要内容，如果未能解决你的问题，请参考以下文章

常用排序快速排序与归并排序

搜索与排序—— 归并排序与快速排序

精益求精单链表归并排序与快速排序

JavaScript算法（归并排序与快速排序）

快速排序与归并排序

PAT：归并排序与快速排序模板