B. Omkar and Last Class of Math1300 / 数论

Posted 2021-12-07 幽殇默

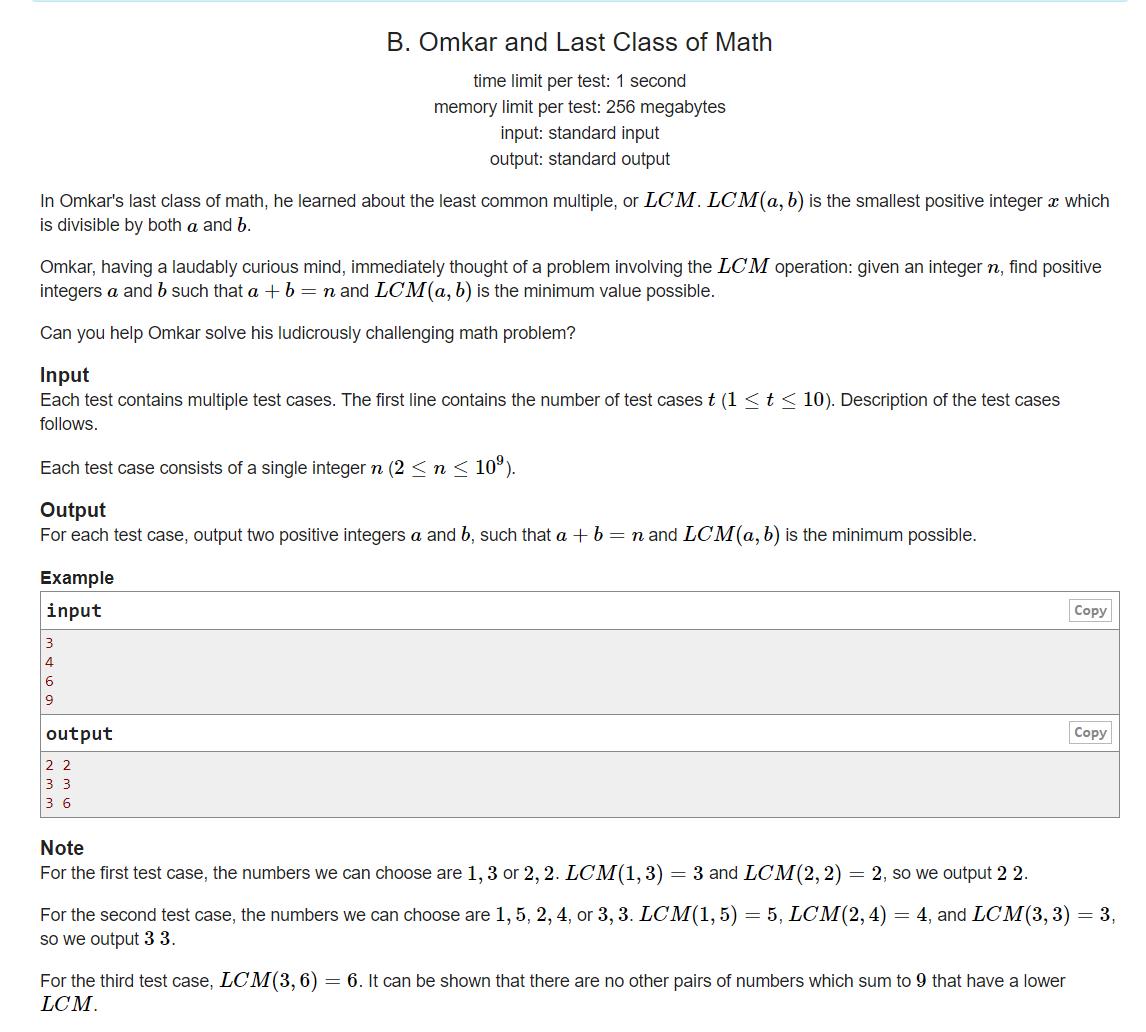
https://codeforces.com/problemset/problem/1372/B
设x是n的因子，a=x，b=n-x,那么就有max(a,b)%min(a,b)=0
那么a，b的最大公倍数便是max(a,b)
例如: 8=2*4 那么可以分成 4 4
例如: 16=4*4 那么可以分成 4 12 必可以是它的约数
随着约数的增大，我们的分的第二份越来越小，越来越是正解。

#include<bits/stdc++.h>
using namespace std;
int main(void)
{
	int t; cin>>t;
	while(t--)
	{
		int n; cin>>n;
		int cnt=n,x=1,y=n-x;
		for(int i=2;i<=n/i;i++)
		{
			if(n%i==0)
			{
				int temp1=n/i,temp2=n-temp1;//总共i份 1份给temp1 (i-1)份给temp2
				if(temp2<=cnt) cnt=temp2,x=temp1,y=temp2;
			}
		}
		cout<<x<<" "<<y<<endl;
	}
	return 0;
}