图像处理：图像的几何变换

Posted 2021-12-07 GeniusAng

图像处理笔记总目录

---

1 图像缩放

缩放是对图像的大小进行调整，即使图像放大或缩小。

API：cv2.resize(src,dsize,fx=0,fy=0,interpolation=cv2.INTER_LINEAR)

参数：

• src : 输入图像
• dsize: 绝对尺寸，直接指定调整后图像的大小
• fx,fy: 相对尺寸，将dsize设置为None，然后将fx和fy设置为比例因子即可
• interpolation：插值方法

插值	含义
cv2.INTER_LINEAR	双线性插值法
cv2.INTER_NEAREST	最近邻插值
cv2.INTER_AREA	像素区域重采样（默认）
cv2.INTER_CUBIC	双三次插值

在缩小时推荐cv2.INTER_ARER，扩大时推荐cv2.INTER_CUBIC和cv2.INTER_LINEAR

示例：

import cv2.cv2 as cv
# 1. 读取图片
img1 = cv.imread("./image/dog.jpeg")
# 2.图像缩放
# 2.1 绝对尺寸
rows,cols = img1.shape[:2]
res = cv.resize(img1,(2*cols,2*rows),interpolation=cv.INTER_CUBIC)

# 2.2 相对尺寸
res1 = cv.resize(img1,None,fx=0.5,fy=0.5)

# 3 图像显示
# 3.1 使用opencv显示图像(不推荐)
cv.imshow("orignal",img1)
cv.imshow("enlarge",res)
cv.imshow("shrink）",res1)
cv.waitKey(0)

# 3.2 使用matplotlib显示图像
fig,axes=plt.subplots(nrows=1,ncols=3,figsize=(10,8),dpi=100)
axes[0].imshow(res[:,:,::-1])
axes[0].set_title("绝对尺度（放大）")
axes[1].imshow(img1[:,:,::-1])
axes[1].set_title("原图")
axes[2].imshow(res1[:,:,::-1])
axes[2].set_title("相对尺度（缩小）")
plt.show()

2 图像平移

图像平移将图像按照指定方向和距离，移动到相应的位置。

API：cv.warpAffine(img,M,dsize)
参数：

• img：输入图像
• M：2 $\ast$ 3移动矩阵
  对于$(x,y)$处的像素点，要把它移动到 $(x+t_x,y+t_y)$ 处时，M矩阵应如下设置：
  $$M=\left[\begin{array}{lll}1& 0& t_x\\ 0& 1& t_y\end{array}\right]$$
  注意：将M设置为np.float32类型的Numpy数组。
• dsize: 输出图像的大小
  注意：输出图像的大小，它应该是(宽度，高度)的形式。请记住,width=列数，height=行数。

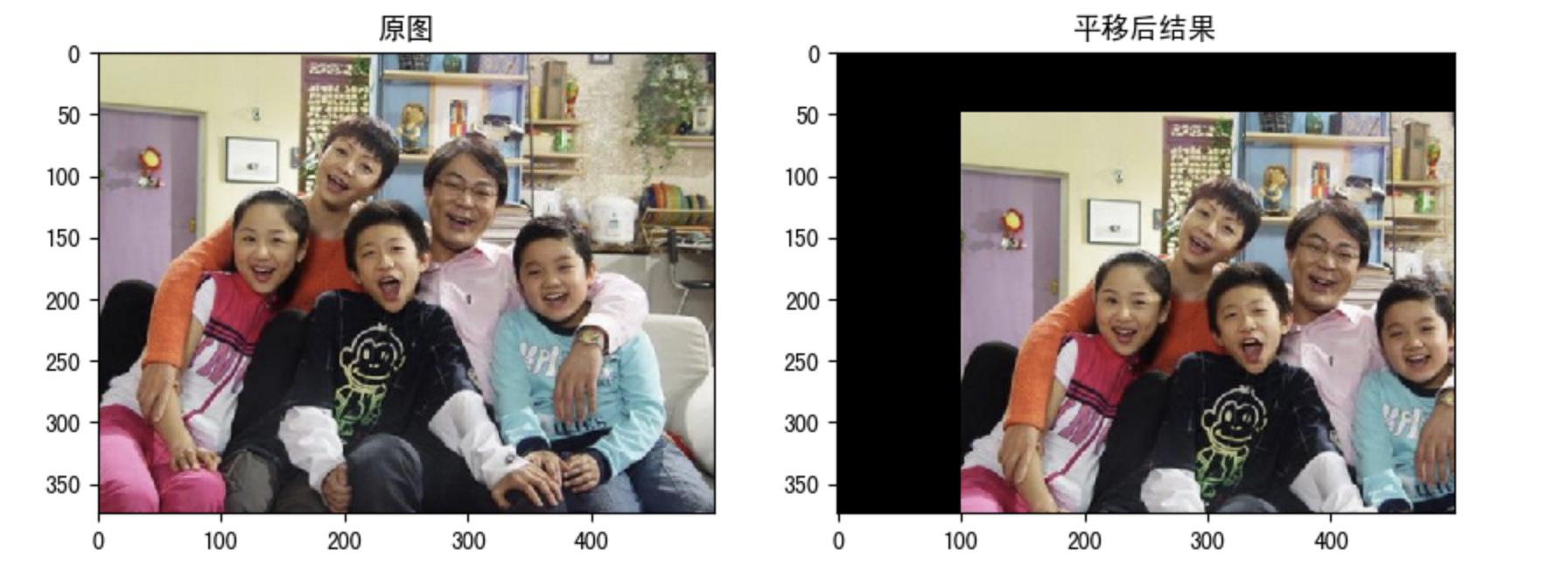
示例：需求是将图像的像素点移动 (100,50) 的距离

import numpy as np
import cv2.cv2 as cv
import matplotlib.pyplot as plt
# 1. 读取图像
img1 = cv.imread("./image/image2.jpg")

# 2. 图像平移
rows,cols = img1.shape[:2]
M = M = np.float32([[1,0,100],[0,1,50]])# 平移矩阵
dst = cv.warpAffine(img1,M,(cols,rows))

# 3. 图像显示
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,8),dpi=100)
axes[0].imshow(img1[:,:,::-1])
axes[0].set_title("原图")
axes[1].imshow(dst[:,:,::-1])
axes[1].set_title("平移后结果")
plt.show()

3 图像旋转

图像旋转是指图像按照某个位置转动一定角度的过程，旋转中图像仍保持这原始尺寸。图像旋转后图像的水平对称轴、垂直对称轴及中心坐标原点都可能会发生变换，因此需要对图像旋转中的坐标进行相应转换。

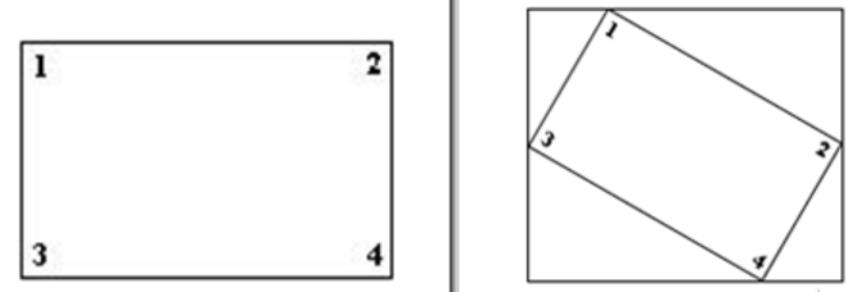
那图像是怎么进行旋转的呢？如下图所示：

假设图像逆时针旋转 $\theta$，则根据坐标转换可得旋转转换为:
$$\{\begin{array}{l}{x}^{\prime }=r\cos (\alpha -\theta )\\ y^{\prime }=r\sin (\alpha -\theta )\end{array}$$

其中：

$$r=\sqrt{x^2+y^2},\sin \alpha =\frac{y}{\sqrt{x^2+y^2}},\cos \alpha =\frac{x}{\sqrt{x^2+y^2}}$$

带入上面的公式中，有：
$$\{\begin{array}{l}{x}^{\prime }=x\cos \theta +y\sin \theta \\ y^{\prime }=-x\sin \theta +y\cos \theta \end{array}$$

也可以写成：
$$\left[\begin{array}{lll}{x}^{\prime }& y^{\prime }& 1\end{array}\right]=\left[\begin{array}{lll}x& y& 1\end{array}\right]\left[\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]$$

同时我们要修正原点的位置，因为原图像中的坐标原点在图像的左上角，经过旋转后图像的大小会有所变化，原点也需要修正。

假设在旋转的时候是以旋转中心为坐标原点的，旋转结束后还需要将坐标原点移到图像左上角，也就是还要进行一次变换。

[ x ′ ′ y ′ ′ 1 ] = [ x ′ y ′ 1 ] [ 1 0 0 0 − 1 0 l e f t  top  1 ] = [ x y 1 ] [ cos ⁡ θ − sin ⁡ θ

以上是关于图像处理：图像的几何变换的主要内容，如果未能解决你的问题，请参考以下文章

几何变换

数字图像处理——图像的几何变换

图像的几何变换

Python图像处理丨带你掌握图像几何变换

图像几何变换之透视变换

OpenCV中的图像处理 —— 改变颜色空间+图像几何变换