数据结构堆

Posted 2021-12-07 凛音Rinne

堆

---

文章目录

• 堆
• • 一、堆的概念
  • 二、堆的实现
  • • 1. 定义节点
    • 2. 堆的初始化
    • 3. 堆的销毁
    • 4. 堆的插入
    • 5. 堆的删除

一、堆的概念

堆是二叉树的一种特殊情况

• 一个堆中的所有节点的值总是不大于或不小于其父节点的值

• 堆是一棵完全二叉树。

• 堆分为大堆和小堆

  大堆：根节点最大的堆叫做最大堆或大根堆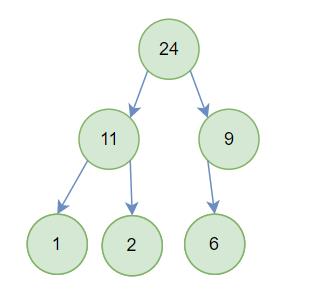

  

  小堆：根节点最小的堆叫做最小堆或小根堆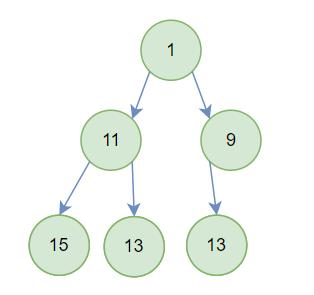

  

普通的二叉树是不适合用数组来存储，因为可能会因为数据不连续而导致存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。

又因为上一篇文章中提出【数据结构】二叉树的定义以及性质_Rinne’s blog-CSDN博客

子节点和父节点序号有一定的联系

这里的堆，我们用数组来实现

---

二、堆的实现

1. 定义节点

我们先确定了用数组的形式来实现，虽然物理上是一个顺序表的样子，但逻辑上我们使用的过程它却是一个堆

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}Heap;

---

2. 堆的初始化

本质上就是顺序表的初始化

//堆的初始化
void HeapInit(Heap* hp)
{
	assert(hp);

	hp->a = NULL;
	hp->capacity = 0;
	hp->size = 0;
}

---

3. 堆的销毁

本质上是顺序表的销毁

// 堆的销毁
void HeapDestory(Heap* hp)
{
	assert(hp);

	free(hp->a);
	hp->capacity = hp->size = 0;
}

---

4. 堆的插入

前面还是跟顺序表一样，插入之前先判断内存空间够不够，不够就malloc

关键在于：

• 如果是一个大堆，插入的数比它的父节点大，我们需要去向上调整
• 如果是一个小堆，插入的数比它的父节点小，我们需要去向上调整

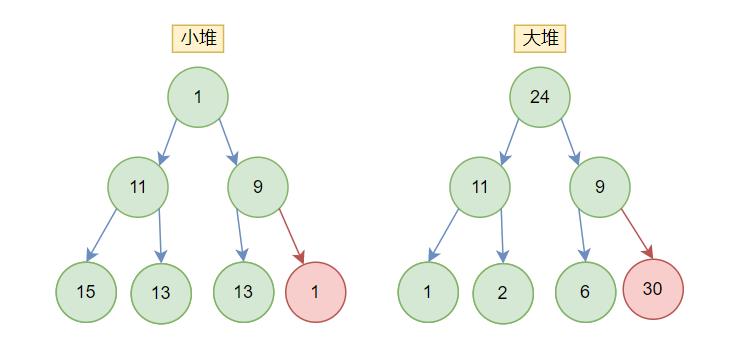
先看大堆

如果子节点比父节点大，交换父子节点

当子节点序号为0时候停止

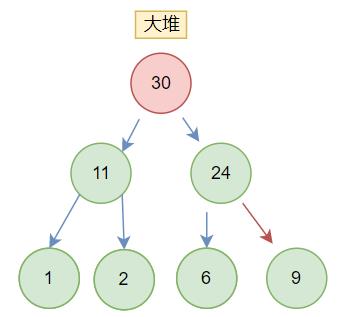
以下是大堆，小堆需要改一下＞符号

//交换数据
void swap(HPDataType* parent, HPDataType* child)
{
	HPDataType tmp = *child;
	*child = *parent;
	*parent = tmp;
}

//向上调整
void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (a[child] > a[parent] && child != 0)
	{
		swap(&a[child], &a[parent]);
		child = parent;
		parent = (child - 1) / 2;
	}
}

// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{
	assert(hp);

	if (hp->size == hp->capacity)
	{
		int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(hp->a, newcapacity * sizeof(HPDataType));
		
		if (tmp == NULL)
		{
			exit(-1);
		}

		hp->a = tmp;
		hp->capacity = newcapacity;
	}

	hp->a[hp->size] = x;
	hp->size++;

	AdjustUp(hp->a, hp->size - 1);
}

测试：

void test1()
{
	Heap h;
	HeapInit(&h);
	HeapPush(&h, 24);
	HeapPush(&h, 11);
	HeapPush(&h, 9);
	HeapPush(&h, 1);
	HeapPush(&h, 2);
	HeapPush(&h, 6);
	HeapPush(&h, 30);

	int i = 0;

	for (i = 0; i < h.size; i++)
	{
		printf("%d ", h.a[i]);
	}

}

测试结果： 可以看出后面插入的30被向上调整到前面去了

---

5. 堆的删除

删除堆是删除堆顶的数据

还是以刚才的例子为例

将堆顶的数据根最后一个数据一换，然后删除数组最后一个数据

为什么不直接删除根呢，根是数组的头，类似顺序表的头删，需要把所有元素向前移动，这就改变了整个树的相对位置，时间复杂度为o(n)，而删除了根之后，我们需要调整位置，找到下一个根，根的子节点，为左右两个孩子，挑出左右孩子中最大的那个

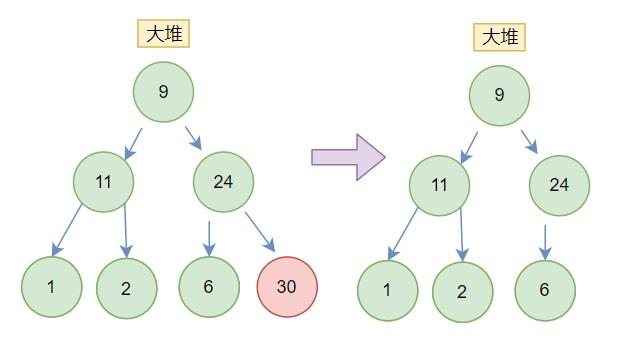
再进行 向下调整算法

//向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{
	int child = parent * 2 + 1;

	while (child < n)
	{
		if (a[child] < a[child + 1] && child + 1 < n)
		{
			child++;
		}

		if (a[parent] < a[child])
		{
			swap(&a[parent], &a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

// 堆的删除
void HeapPop(Heap* hp)
{
	assert(hp);
	assert(hp->size);

	swap(&hp->a[0], &(hp->a[hp->size - 1]));
	hp->size--;

	//删完后开始调整
	AdjustDown(hp->a, hp->size, 0);

}

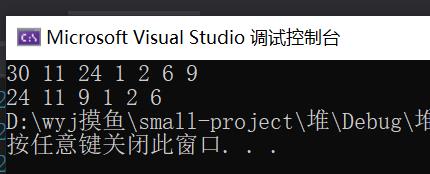
在插入的测试代码基础上再删除根

测试结果：

---