数据结构二叉树的定义以及性质

Posted 2021-12-07 凛音Rinne

二叉树

文章目录

• 二叉树
• • 一、树
  • • 1.树的定义
    • 2. 树的概念
    • • (1) 节点的度
      • (2) 叶节点(终端节点)
      • (3) 分支节点(非终端节点)
      • (4) 父节点(双亲节点)
      • (5) 子节点(孩子节点)
      • (6) 兄弟节点
      • (7) 树的度
      • (8) 节点的层次
      • (9) 树的高度(深度)
      • (10) 堂兄弟节点
  • 二、二叉树
  • • 1. 树的表示
    • 2. 二叉树
    • 3. 二叉树的种类
    • • (1) 满二叉树
      • (2) 完全二叉树
    • 4. 二叉树的性质

二叉树

在了解二叉树之前，专业外的人，比如我，二叉树的名称早就听说过，在了解二叉树之前，应当先去了解树的几个概念，毕竟，二叉树是普通树中特殊的存在

一、树

1.树的定义

树是一种 非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。

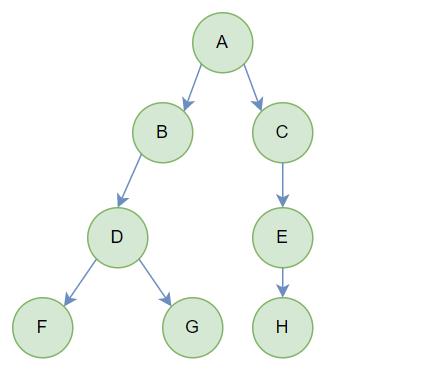
• B 和 C 是 A 的子节点
• 有一个特殊的结点(A)，称为根结点，根节点没有前驱结点
• 子树之间不能有交集，否则就不是树形结构

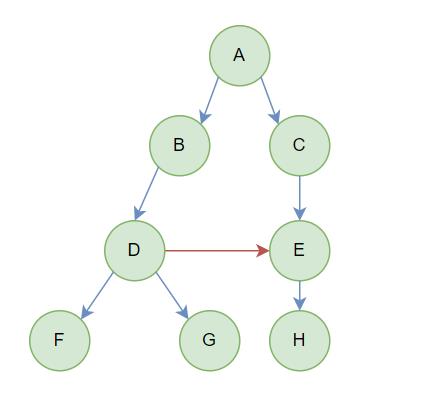
2. 树的概念

树的概念还是很多专有名词的，还是得多看几遍才能记住

(1) 节点的度

一个节点含有的子树的个数称为该节点的度

---

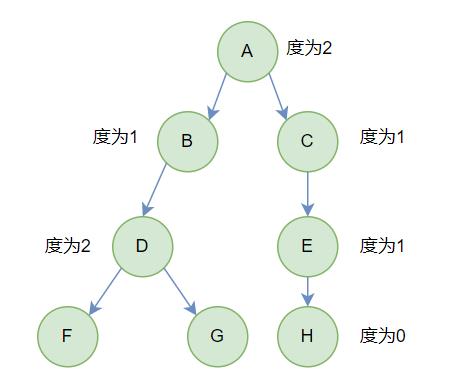
(2) 叶节点(终端节点)

度为0的节点称为叶节点

---

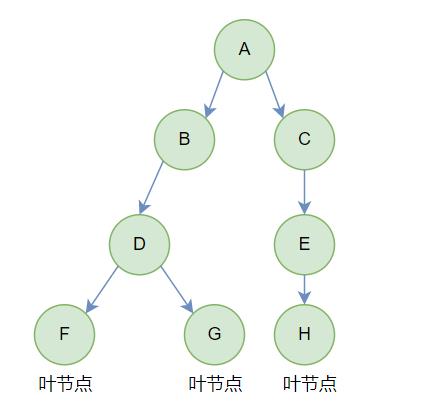
(3) 分支节点(非终端节点)

不为0的节点

---

(4) 父节点(双亲节点)

若一个节点含有子节点，则这个节点称为其子节点的父节点

A 是 B 和 C 的 父节点

---

(5) 子节点(孩子节点)

一个节点含有的子树的根节点称为该节点的子节点

B 和 C 是 A 的 子节点

---

(6) 兄弟节点

具有相同父节点的节点互称为兄弟节点

B 和 C 互为 兄弟节点

---

(7) 树的度

最大的 节点的度 称为树的度

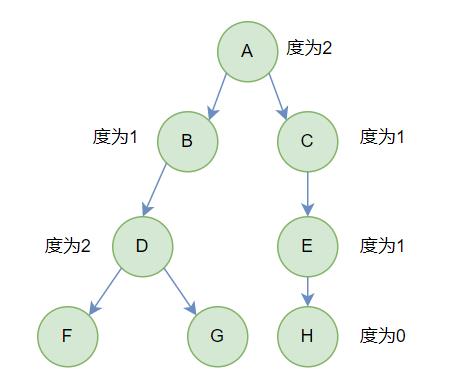
这个数最大的度为2，所以树的度也为2

---

(8) 节点的层次

从根开始定义起，根为第1层，根的子节点为第2层，依次递增

---

(9) 树的高度(深度)

树中节点的最大层次

比如例子中树的高度为4

---

(10) 堂兄弟节点

双亲在同一层的节点互为堂兄弟

比如例子中的G 和 H

---

二、二叉树

如果要写一个二叉树的话，先了解一下树是怎么写的

1. 树的表示

既要保存值域，也要保存结点和结点之间的关系

树有很多种表示方式如：双亲表示法，孩子表示法、孩子双亲表示法以及孩子兄弟表示法等

我们这里就简单的了解其中最常用的孩子兄弟表示法

typedef int DataType;
struct Node
{
 struct Node* Child;//第一个孩子结点
 struct Node* Brother;//指向其下一个兄弟结点
 DataType data; //结点中的数据域
};

图解：

---

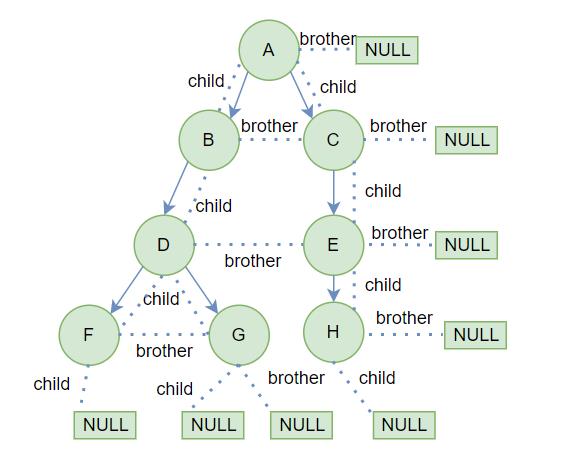
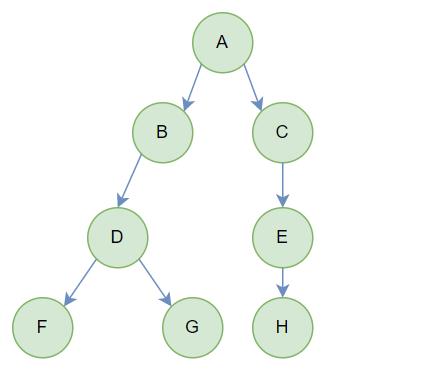
2. 二叉树

• 度最大为2的树
• 有左右之分，左边为左孩子，右边为右孩子

---

3. 二叉树的种类

(1) 满二叉树

每个节点的度都是2，则这个二叉树就是满二叉树。

如果一个二叉树的层数为K，且结点总数是2^k - 1，则它就是满二叉树

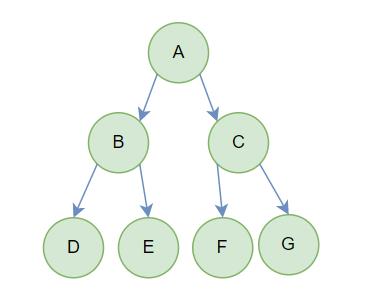
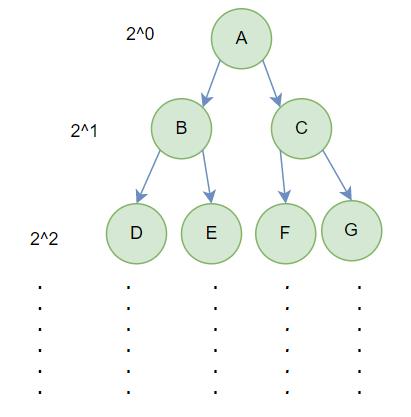
用等比数列求和公式，得出所有的节点加起来是2^k - 1

---

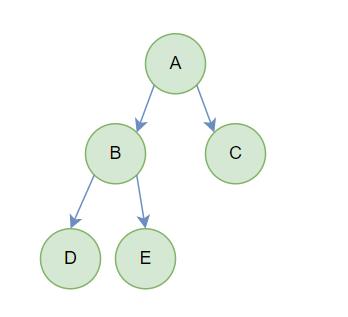
(2) 完全二叉树

简单来说二叉树中元素是连续的，

如图：

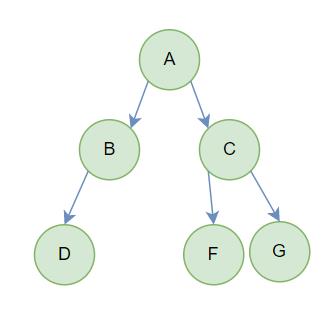
错误图示：

---

4. 二叉树的性质

• 二叉树的 i 行最多有 2^h-1个节点

• 深度为h的二叉树，节点数最多有 2^h -1

• 对任何一棵二叉树, 如果度为0其叶结点个数为 n0 , 度为2的分支结点个数为 n2

  证明: 除了根节点A其他每个节点都有一个从上往下的箭头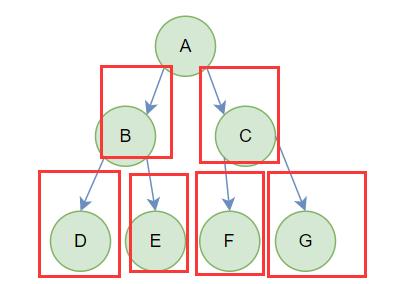

  

  单独挑出来，放大了看，这是每有一个度为1的节点，有一个箭头向下：

  

  每有一个度为2的节点就有两个箭头，向下

  

  先设

  • 一共有n个节点

  • 度为0的节点有n0个

  • 度为1的节点有n1个

  • 度为2的节点有n2个

  节点数的两个式子：

  n = n1 + n2 + n0

  而 度为0 的没有这个箭头，我们拿这个箭头去算

  箭头个数的式子

  n - 1 = n1 + 2n2

  两个式子联立

  得出 n0 = n2 + 1

• 若规定根节点的层数为1，具有n个结点的满二叉树的深度为log2(n + 1)

• 父亲序号为i，找左右孩子

  因为每层节点的个数成指数型增长

  2⁰、2¹、2²……

  

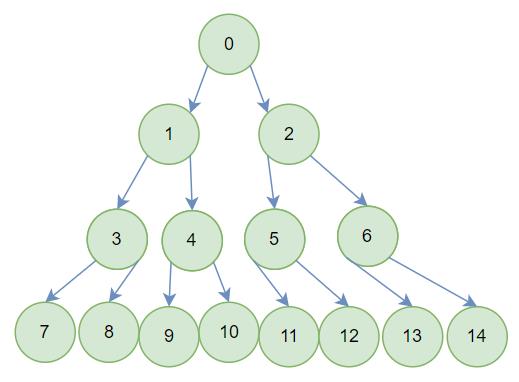
  可以看出左孩子序号是父亲序号的2倍 + 1

  可以看出右孩子序号是父亲序号的2倍 + 2

• 孩子序号为i，找父亲，反之就行，父亲为 (i - 1)/2

---