恒源云_CAN: 借助数据分布提升分类性能

Posted 2021-12-06 AI酱油君

文章来源 | 恒源云社区（专注人工智能/深度学习GPU免费加速平台，官方体验网址：https://gpushare.com）

原文作者 | Mathor

原文地址 | https://gpushare.com/forum/topic/683/can-%E5%80%9F%E5%8A%A9%E6%95%B0%E6%8D%AE%E5%88%86%E5%B8%83%E6%8F%90%E5%8D%87%E5%88%86%E7%B1%BB%E6%80%A7%E8%83%BD?_=1635993190297

本文将介绍一种用于分类问题的后处理技巧（Trick），出自EMNLP 2021 Findings的一篇论文《When in Doubt: Improving Classification Performance with Alternating Normalization》。经过实测，CAN（Classification with Alternating Normalization）确实多数情况下能提升多分类问题的效果（CV、NLP通用），而且几乎没有增加预测成本，因为它仅仅只是对预测结果的重新归一化操作

---

CAN的思想

有趣的是，其实CAN的思想非常朴素，朴素到我们每个人几乎都用过。具体来说，假设考试中有10道选择题，前9道你都比较有信心，第10题完全不会只能瞎蒙，但是你发现前面9题选A、B、C、D的比例是3:3:2:2，那么第10题在蒙的时候，你会不会更倾向于C和D？如果是更极端的情况，你发现前面9题选A、B、C的都有，但就是没有选D的，那你蒙第10题的时候，会不会更倾向于D？

回到分类任务上，假设现在有一个二分类问题，模型对于输入aaa给出的预测结果是$p^{(a)}=[0.05,0.95]$，那么我们就可以给出预测类别为1；接下来，对于输入bbb，模型给出的预测结果是$p^{(b)}=[0.5,0.5]$，这种结果是最不确定的，我们也不知道应该输出哪个类别

但是，假如我告诉你：

1. 类别必然是0或1其中之一
2. 两个类别出现的概率各为0.5

在已知这两点「先验」信息的情况下，由于前一个样本的预测结果为1，那么基于朴素的均匀思想，我们是否会更倾向于将后一个样本预测为0，以得到一个满足第二点「先验」的预测结果？

这些简单的例子背后，有着跟CAN同样的思想，其实就是用**「先验分布」来校正「低置信度」的预测结果，使得新的预测结果的分布更接近先验分布**

TOP-K熵

准确地说，CAN是针对低置信度预测结果的后处理手段，所以我们首先要有一个衡量预测结果不确定性的指标。常见的度量是「熵」，对于$p=[p_1,p_2,\dots ,p_m]$ ，定义为

虽然熵是一个常见的选择，但其实它得出的结果并不总是符合我们的直观理解。例如对于$p^{(a)}=[0.5,0.25,0.25]和p^{(b)}=[0.5,0.5,0]$，直接套用公式得到$H(p^{(b)})H(p^{(b)})$，但如果让人主观去评价这两个概率分布，显然我们会认为$p^{(b)}比p^{(a)}$更不确定，所以直接用熵还不够合理

客观地讲，熵值越大，表示这个系统内部越不稳定。如果要与置信度联系起来，熵值越大，置信度越低

一个简单的修正是只用前top-k个概率值来算熵，假设$p_1,p_2,\dots ,p_k$是概率最高的$k$个值，那么

其中，$\mathcal{T}$是一个取向量最大的前k个值的操作$R^m$→$R^k$。我们可以将式(2)带入式(1)展开得

其中，$pi=p_i/\sum _{i=1}^k{p}_i$

交替归一化（ALTERNATING NORMALIZATION）

这一部分我先给出论文中的算法步骤描述，下一节我会手动模拟一遍计算过程

Step1

设列向量${\mathbf{b}}_0\in {\mathbb{R}}^m$为输入样本$x$对应各类别的概率分布，$m$表示类别数。我们生成一个$n$×$m$的概率矩阵$A_0，A_0$其实是$n$个置信度非常高的样本对各个类别的预测概率向量拼接而得，通过将$A_0和{\mathbf{b}}_0$进行拼接得到一个$(n+1)\times m$的矩阵 $L_0$

Step2

第二步是一个迭代的过程，具体来说，首先对矩阵$L_0$进行列归一化（使得每列求和为1），然后进行行归一化（使得每行求和为1）。进行算法步骤前，先定义一个向量对角化操作：

D(v)会将列向量$\mathbf{v}\in {\mathbb{R}}^n$转换为$n\times n$的对角矩阵，对角线元素即原本的向量元素

列归一化
​
其中，参数$\alpha \in {\mathbb{N}}^{+}$控制着${\mathbf{b}}_0$收敛到高置信度的速度（越大速度越快，默认取1）；$\mathbf{e}\in {\mathbb{R}}^{n+1}$是全1的列向量。经过式(4)的变换后，矩阵$S_d\in {\mathbb{R}}^{(n+1)\times m}$是$L_{d-1}$矩阵的列归一化形式；${\Lambda }_S^{-1}$是${\Lambda }_S$的逆矩阵

行归一化

其中，$\mathbf{e}\in {\mathbb{R}}^m$仍然是全1的列向量，只不过此时它的维度是mmm维的；矩阵$L_d\in {\mathbb{R}}^{(n+1)\times m}$是行归一化的（但$L_d$并不是具体某个矩阵的行归一化形式）；${\Lambda }_q\in {\mathbb{R}}^{m\times m}$是一个对角矩阵，对角线上的元素是各类别的分布占比

例如

表示这是一个三分类问题，并且各个类别的比例为1:2:2

Step3

Step2循环迭代ddd次后得到的矩阵$L_d$：

其中，${\mathbf{b}}_d$就是根据「先验分布」调整后的新的概率分布

注意，这个过程需要我们遍历每个低置信度的预测结果，也就是说逐个样本进行修正，而不是一次性修正的。并且虽然迭代过程中$A_0$里对应的各个样本的预测概率也都随之更新了，但那只是临时结果，最后都是弃之不用的，每次修正都是用原始的$A_0$

模拟计算AN（ALTERNATING NORMALIZATION）

首先我们设置一些矩阵和参数
​
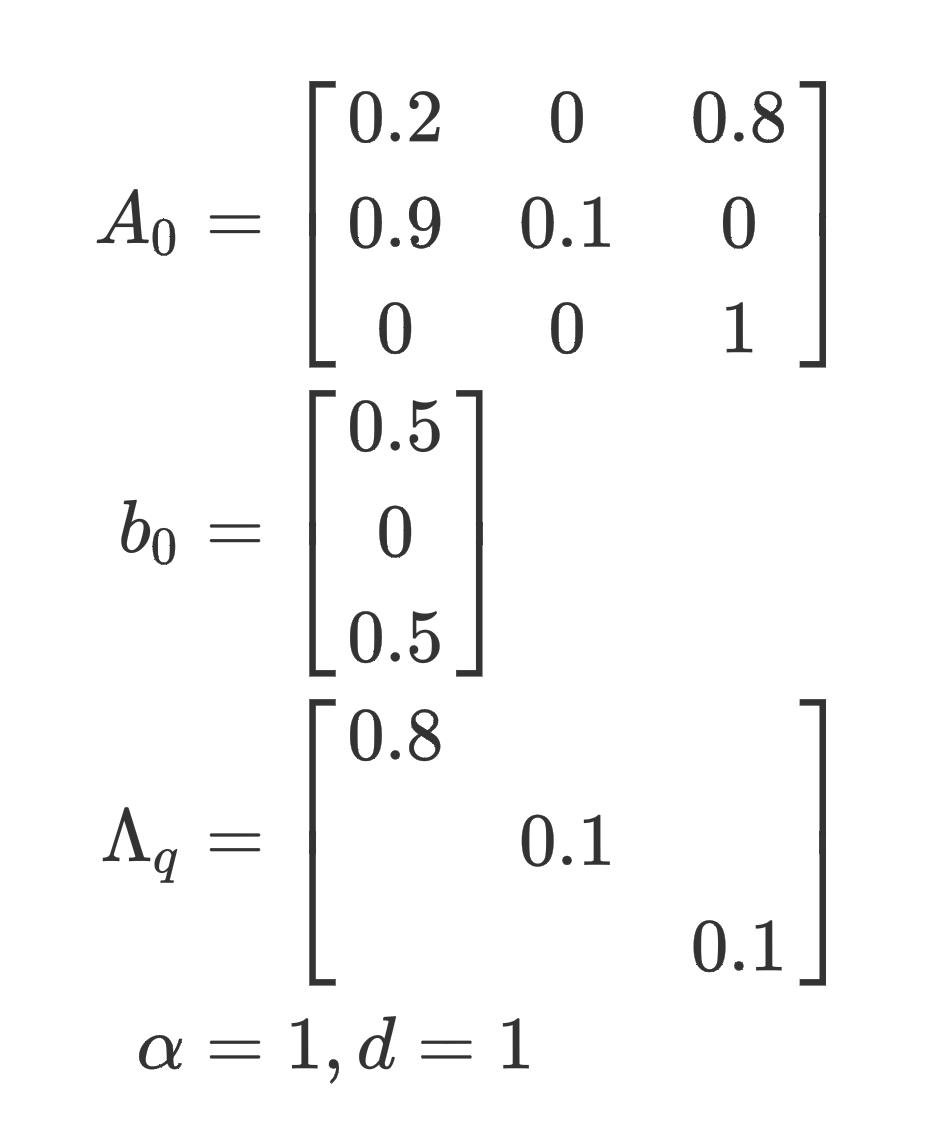
稍微解释一下，$A_0$根据原算法描述是nnn个置信度比较高的样本的预测概率分布进行拼接，可以看出只有3个样本置信度比较高，并且他们的预测类别分别为2，0，2；$b_0$

恒源云_云GPU服务器如何使用LightGBM？

恒源云_[文本分类] 文本数据增强1(论文笔记)

阿里推出 PolarFS 分布式文件系统：将存储与计算分开，提升云数据库性能（附论文）

恒源云(GpuShare)_MaskFormer：语义分割可以不全是像素级分类

恒源云(GpuShare)_MaskFormer：语义分割可以不全是像素级分类

深度学习训练 | 如何在云服务器上安装LightGBM