matlab取送货路径优化

Posted 2021-12-06 张叔zhangshu

问题描述

假设快递集散中心负责n个配送点的快递配送任务以及包装回收，每个配送点都配备了快递柜以及快递包装回收容器，配送点工作人员在负责快递柜的投放工作以及寄件服务的同时还负责废旧包装的打包工作。快递运输车辆从快递集散中心出发向配送点配发快件并收取配送点需邮寄的快件和打包好的快递包装，快递运输车辆在完成配送任务后返回快递集散中心并卸载需邮寄的快件和打包好的快递包装，快递集散中心负责将卸载的快件向上一级配送中心邮寄并把回收的快递包装整合交给废旧包装回收公司。

体积	25 立方米
百公里油耗	60元/9.5L/6.65kg
燃油二氧化碳排放系数	3.1705 kg-co2/kg
碳税	10元/吨
车辆平均行驶速度	40km/h
包装回收载货空间	0.1立方米
快递存放载货空间	3.4立方米
单位快递容积	0.027立方米
单位快递包装容积	0.0008立方米
固定成本	18.6元/辆*天

符号说明

模型假设

假设1：快递包装为标准规格包装；
假设2：不考虑不同路面及交通延误对配送方案的影响；
假设3：配送车辆均为标准规格的快递配送车；
假设4：不考虑各配送点的时间窗约束；
假设5：各配送点均自行负责回收的快递包装打包工作，因此配送方案不考虑回收的快递包装打包产生的人工费用，
模型建立

假设某一快递配送中心为27个配送点配送和收取快递同时收取废旧包装[13]，各配送点及配送中心的位置和货物信息如下表所示；运送的快件多为4号标准规格的包装，即360×300×250MM规格包装，因此本文将所有快件都视为此规格的快件，回收的包装材料也打包为同等规格的包装，具体参数如下表所示。

客户	横坐标	纵坐标	配送量/件	取件量/件	回收量/件
0	11	11	0	0	0
1	46	10	160	130	148
2	16	29	260	270	214
3	18	7	100	125	89
4	13	43	400	333	389
5	13	39	120	112	105
6	19	30	160	185	152
7	1	36	120	157	111
8	27	7	200	226	187
9	32	4	350	433	326
10	20	5	650	467	614
11	38	35	180	118	163
12	50	12	240	130	227
13	37	30	420	222	396
14	20	48	420	400	374
15	21	31	180	109	152
16	14	15	120	235	112
17	11	40	400	406	388
18	42	27	270	238	259
19	50	49	200	124	187
20	21	23	80	106	69
21	8	23	220	150	205
22	27	5	240	160	215
23	41	17	360	305	317
24	14	31	280	229	265
25	11	50	280	151	269
26	18	11	150	109	148
27	31	42	500	640	492

车型	百公里燃油消耗	容量	平均使用年限	购置税
轻型卡车	60元	25立方米	8	54270元

tic
clear
clc
%% 用importdata这个函数来读取文件 
load('data1');
cap=25;
%% 提取数据信息
vertexs=data(:,2:3);                %所有点的坐标x和y
customer=vertexs(2:end,:);          %顾客坐标
cusnum=size(customer,1);            %顾客数
v_num=16;                           %初始车辆使用数目
demands=data(2:end,4);              %需求量
qujian=data(2:end,5);%取件量
huishou=data(2:end,5);%回收量
h=pdist(vertexs);
dist=squareform(h);                 %距离矩阵
%% 遗传算法参数设置
alpha=1000;                                                       %违反的容量约束的惩罚函数系数
NIND=200;                                                        %种群大小
MAXGEN=1000;                                                     %迭代次数
Pc=0.9;                                                         %交叉概率
Pm=0.05;                                                        %变异概率
GGAP=0.9;                                                       %代沟(Generation gap)
N=cusnum+v_num-1;                                               %染色体长度=顾客数目+车辆最多使用数目-1
%% 种群初始化
Chrom=InitPop(NIND,N);
%% 输出随机解的路线和总距离
disp('初始种群中的一个随机值:')
[currVC,NV,TD]=decode(Chrom(1,:),cusnum,cap,demands,dist);       %对初始解解码
currCost=costFuction(currVC,dist,demands,cap,alpha,NV,qujian,huishou);        %求初始配送方案的成本=车辆行驶总成本+alpha*违反的容量约束之和
disp(['车辆使用数目：',num2str(NV),'，车辆行驶总距离：',num2str(TD)]);
disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~')
%% 优化
BestCost=zeros(MAXGEN,1);       %记录每一代全局最优解的总成本
gen=1;
while gen<=MAXGEN
    %% 计算适应度
    ObjV=calObj(Chrom,cusnum,cap,demands,dist,alpha,qujian,huishou);                           %计算种群目标函数值
    FitnV=Fitness(ObjV);
    %% 选择
    SelCh=Select(Chrom,FitnV,GGAP);
    %% OX交叉操作
    SelCh=Recombin(SelCh,Pc);
    %% 变异
    SelCh=Mutate(SelCh,Pm);
    %% 局部搜索操作
%     SelCh=LocalSearch(SelCh,cusnum,cap,demands,dist,alpha,qujian,huishou);
    %% 重插入子代的新种群
    Chrom=Reins(Chrom,SelCh,ObjV);
%     %% 删除种群中重复个体，并补齐删除的个体
%     Chrom=deal_Repeat(Chrom);
    %% 打印当前最优解
    ObjV=calObj(Chrom,cusnum,cap,demands,dist,alpha,qujian,huishou);                           %计算种群目标函数值
    [minObjV,minInd]=min(ObjV);
    BestCost(gen)=minObjV;
    disp(['第',num2str(gen),'代最优解:'])
    [bestVC,bestNV,bestTD]=decode(Chrom(minInd(1),:),cusnum,cap,demands,dist);
    disp(['车辆使用数目：',num2str(bestNV),'，车辆行驶总距离：',num2str(bestTD)]);
    fprintf('\\n')
    %% 更新迭代次数
    gen=gen+1 ;
end
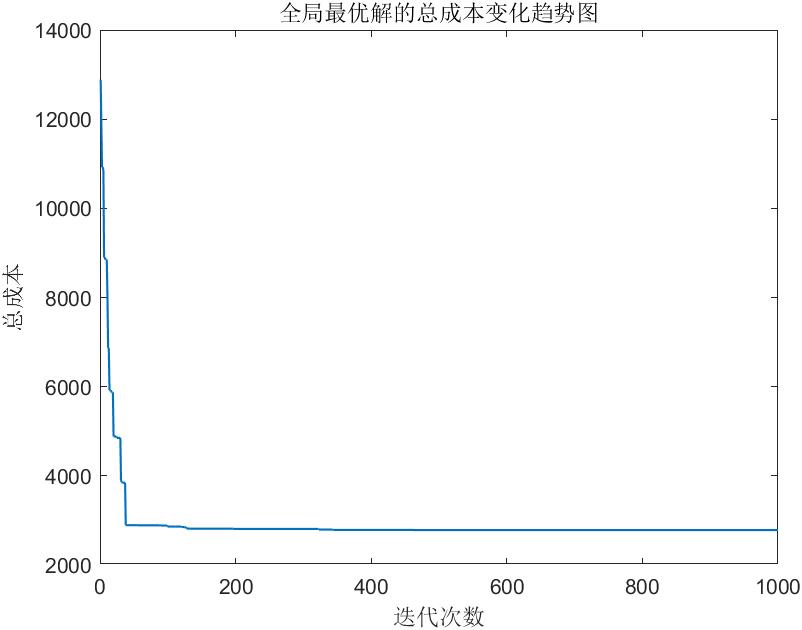
%% 打印外层循环每次迭代的全局最优解的总成本变化趋势图
figure;
plot(BestCost,'LineWidth',1);
title('全局最优解的总成本变化趋势图')
xlabel('迭代次数');
ylabel('总成本');
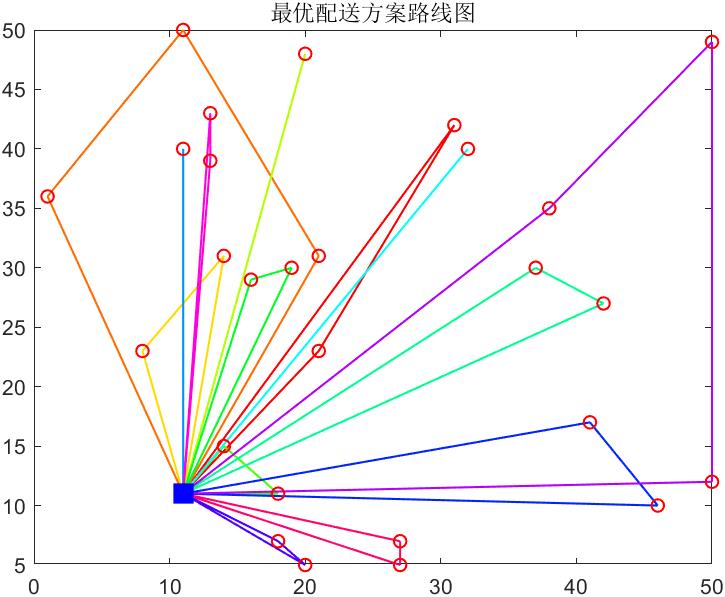
%% 打印全局最优解路线图
draw_Best(bestVC,vertexs);
toc
VX：zhangshu2274