用opencv实现的PCA算法，非API调用

Posted 2020-09-21 mthoutai

理论參考文献：但此文没有代码实现。这里自己实现一下，让理解更为深刻

问题：如果在IR中我们建立的文档-词项矩阵中，有两个词项为“learn”和“study”，在传统的向量空间模型中，觉得两者独立。

然而从语义的角度来讲。两者是相似的。并且两者出现频率也类似，是不是能够合成为一个特征呢？

       《模型选择和规则化》谈到的特征选择的问题。就是要剔除的特征主要是和类标签无关的特征。比方“学生的名字”就和他的“成绩”无关，使用的是互信息的方法。

       而这里的特征非常多是和类标签有关的，但里面存在噪声或者冗余。

在这样的情况下，须要一种特征降维的方法来降低特征数。降低噪音和冗余，降低过度拟合的可能性。

        PCA的思想是将n维特征映射到k维上（k<n）。这k维是全新的正交特征。

这k维特征称为主元，是又一次构造出来的k维特征，而不是简单地从n维特征中去除其余n-k维特征。

         ＰＣＡ计算过程：

  如果我们得到的2维数据例如以下：

     

  行代表了例子。列代表特征，这里有10个例子，每一个例子两个特征。能够这样觉得。有10篇文档，x是10篇文档中“learn”出现的TF-IDF。y是10篇文档中“study”出现的TF-IDF。

第一步 分别求x和y的平均值，然后对于全部的例子。都减去相应的均值。这里x的均值是1.81。y的均值是1.91，那么一个例子减去均值后即为（0.69,0.49），得到

     

      第二步 ，求特征协方差矩阵。假设数据是3维。那么协方差矩阵是

     

     这里仅仅有x和y，求解得

     

     对角线上各自是x和y的方差，非对角线上是协方差。

协方差是衡量两个变量同一时候变化的变化程度。协方差大于0表示x和y若一个增。还有一个也增；小于0表示一个增，一个减。假设ｘ和ｙ是统计独立的。那么二者之间的协方差就是０；可是协方差是０，并不能说明ｘ和ｙ是独立的。协方差绝对值越大，两者对彼此的影响越大。反之越小。协方差是没有单位的量，因此，假设相同的两个变量所採用的量纲发生变化，它们的协方差也会产生树枝上的变化。

    第三步 。求协方差的特征值和特征向量。得到

     

     上面是两个特征值，以下是相应的特征向量，特征值0.0490833989相应特征向量为 。这里的特征向量都归一化为单位向量。

     第四步 ，将特征值依照从大到小的顺序排序。选择当中最大的k个。然后将其相应的k个特征向量分别作为列向量组成特征向量矩阵。

     这里特征值仅仅有两个，我们选择当中最大的那个，这里是1.28402771，相应的特征向量是 。

      第五步 ，将样本点投影到选取的特征向量上。如果例子数为m，特征数为n，减去均值后的样本矩阵为DataAdjust(m*n)。协方差矩阵是n*n。选取的k个特征向量组成的矩阵为EigenVectors(n*k)。那么投影后的数据FinalData为

     

     这里是

     FinalData(10*1) = DataAdjust(10*2矩阵)×特征向量

     得到结果是

     

     这样，就将原始例子的n维特征变成了k维，这k维就是原始特征在k维上的投影。

详细代码例如以下：

#include<cv.h>
#include "opencv2/core/core.hpp"
#include "opencv2/contrib/contrib.hpp"
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/objdetect/objdetect.hpp"
using namespace std;
using namespace cv;

void printMat(CvMat* matric)
{
  int row = matric->rows,col = matric->cols,i,j;
  for(i = 0;i < row;i++)
  {
    for(j = 0;j < col;j++)
    {
      float num = cvGet2D(matric,i,j).val[0];
      cout << num << " ";
    }
    cout << endl;
  }
}
int main()
{
  printf("-------输入原矩阵的行和列-----------\\n");
  int row,col,i,j;
  cin >> row >> col;
  float* data = new float [row*col];
  printf("-------输入原矩阵的元素-------------\\n");
  for(i = 0;i < col;i++)
  {
    for(j = 0;j < row;j++)cin >> data[j * col + i]; 
  }
  CvMat* inputs = cvCreateMat(row,col,CV_32FC1);
  cvSetData(inputs,data,inputs->step);
  printf("------输入的矩阵为------------------\\n");
  printMat(inputs);
  CvMat* means = cvCreateMat(1,col,CV_32FC1);//均值
  CvMat* EigenValue = cvCreateMat(col,1,CV_32FC1);//特征值
  CvMat* EigenVector = cvCreateMat(col,col,CV_32FC1);//特征向量


//	eigen(inputs,EigenValue,EigenVector);

  cvCalcPCA(inputs,means,EigenValue,EigenVector,CV_PCA_DATA_AS_ROW);//以行作为特征维数计算PCA的參数
  printf("-------------均值为-----------------\\n");
  printMat(means);
  printf("-------------特征值为---------------\\n");
  printMat(EigenValue);
  printf("-------------特征向量为-------------\\n");
  printMat(EigenVector);
  printf("-----输入PCA的降维系数。按特征值总和的比例确定PCA的维度，大小在0~1之间------\\n");
  float rate;
  cin >> rate;
  float EigenValueSum = cvSum(EigenValue).val[0],curSum = 0.0;
  for(i = 0;i < col;i++)
  {
    curSum += cvGet2D(EigenValue,i,0).val[0];//cvCalcPCA求出的特征值和特征向量都是排好序的。能够直接使用
    if(curSum > EigenValueSum * rate)break;
  }
  int postDim = i;
  cout << "----从原来的 " << col <<" 维降到 " << postDim << " 维"<<endl;
  CvMat* postEigenVector = cvCreateMat(col,postDim,CV_32FC1);//取前k个特征向量组成的投影矩阵
  CvMat sub;
  cvGetSubRect(EigenVector,postEigenVector,cvRect(0,0,postDim,col));
  for(i = 0;i < row;i++)
  {
    cvGetSubRect(inputs,⊂,cvRect(0,i,col,1));
    cvSub(⊂,means,⊂);
  }
  printf("------------投影矩阵为------------\\n");
  printMat(postEigenVector);
  printf("-----------原矩阵单位化后为----------\\n");
  printMat(inputs);
  CvMat* output = cvCreateMat(row,postDim,CV_32FC1);
  cvmMul(inputs,postEigenVector,output);//cvMul 是多维向量的点乘,cvmMul 是矩阵乘
  printf("-----------PCA处理后的结果为---------\\n");
  printMat(output);

  delete[] data;
  cvReleaseMat(&inputs);
  cvReleaseMat(&means);
  cvReleaseMat(&EigenValue);
  cvReleaseMat(&EigenVector);
  cvReleaseMat(&postEigenVector);
  cvReleaseMat(&output);
  return 0;
}

例子測试：

fangjian@fangjian:~/study/code$ ./opencv 

-------输入原矩阵的行和列-----------

10 2

-------输入原矩阵的元素-------------

2.5 0.5 2.2 1.9 3.1 2.3 2 1 1.5 1.1 2.4 0.7 2.9 2.2 3.0 2.7 1.6 1.1 1.6 0.9

------输入的矩阵为------------------

2.5 2.4 

0.5 0.7 

2.2 2.9 

1.9 2.2 

3.1 3 

2.3 2.7 

2 1.6 

1 1.1 

1.5 1.6 

1.1 0.9 

-------------均值为-----------------

1.81 1.91 

-------------特征值为---------------

1.15562 

0.044175 

-------------特征向量为-------------

0.677873 0.735179 

0.735179 -0.677873 

-----输入PCA的降维系数，按特征值总和的比例确定PCA的维度。大小在0~1之间------

0.98

----从原来的 2 维降到 1 维

------------投影矩阵为------------

0.677873 

0.735179 

-----------原矩阵单位化后为----------

0.69 0.49 

-1.31 -1.21 

0.39 0.99 

0.0899999 0.29 

1.29 1.09 

0.49 0.79 

0.19 -0.31 

-0.81 -0.81 

-0.31 -0.31 

-0.71 -1.01 

-----------PCA处理后的结果为---------

0.82797 

-1.77758 

0.992197 

0.27421 

1.6758 

0.912949 

-0.0991095 

-1.14457 

-0.438046 

-1.22382 

注意，输入的降维比例要足够大，至少保证有1维 ，这里使用的是0.98

上面的数据能够觉得是learn和study特征融合为一个新的特征叫做LS特征，该特征基本上代表了这两个特征。

  上述过程有个图描写叙述：

     

     正号表示预处理后的样本点，斜着的两条线就各自是正交的特征向量（因为协方差矩阵是对称的。因此其特征向量正交）。最后一步的矩阵乘法就是将原始样本点分别往特征向量相应的轴上做投影。

     假设取的k=2。那么结果是

     

     这就是经过PCA处理后的样本数据，水平轴（上面举例为LS特征）基本上能够代表所有样本点。

整个过程看起来就像将坐标系做了旋转，当然二维能够图形化表示，高维就不行了。

上面的假设k=1，那么仅仅会留下这里的水平轴，轴上是所有点在该轴的投影。

     这样PCA的过程基本结束。

在第一步减均值之后，事实上应该另一步对特征做方差归一化。比方一个特征是汽车速度（0到100）。一个是汽车的座位数（2到6），显然第二个的方差比第一个小。因此，假设样本特征中存在这样的情况，那么在第一步之后，求每一个特征的标准差  。然后对每一个例子在该特征下的数据除以  。

     归纳一下，使用我们之前熟悉的表示方法，在求协方差之前的步骤是：

     

     当中  是例子，共m个。每一个例子n个特征，也就是说  是n维向量。  是第i个例子的第j个特征。  是例子均值。  是第j个特征的标准差。

     整个PCA过程貌似及其简单。就是求协方差的特征值和特征向量，然后做数据转换。可是有没有认为非常奇妙。为什么求协方差的特征向量就是最理想的k维向量？其背后隐藏的意义是什么？整个PCA的意义是什么？

 PCA理论基础

     要解释为什么协方差矩阵的特征向量就是k维理想特征。我看到的有三个理论：各自是最慷慨差理论、最小错误理论和坐标轴相关度理论。这里简单探讨前两种，最后一种在讨论PCA意义时简单概述。

 最慷慨差理论

     在信号处理中觉得信号具有较大的方差。噪声有较小的方差。信噪比就是信号与噪声的方差比。越大越好。如前面的图，样本在横轴上的投影方差较大，在纵轴上的投影方差较小，那么觉得纵轴上的投影是由噪声引起的。

因此我们觉得，最好的k维特征是将n维样本点转换为k维后。每一维上的样本方差都非常大。

     比方下图有5个样本点：（已经做过预处理，均值为0。特征方差归一）

     

     以下将样本投影到某一维上，这里用一条过原点的直线表示（前处理的过程实质是将原点移到样本点的中心点）。

     

     如果我们选择两条不同的直线做投影，那么左右两条中哪个好呢？依据我们之前的方差最大化理论。左边的好。由于投影后的样本点之间方差最大。

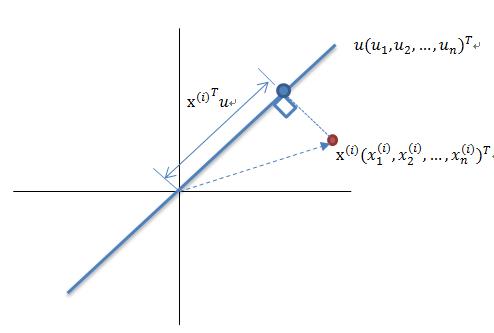
     这里先解释一下投影的概念：

     

     红色点表示例子  。蓝色点表示  在u上的投影，u是直线的斜率也是直线的方向向量，并且是单位向量。蓝色点是  在u上的投影点。离原点的距离是 （即  或者  ）因为这些样本点（例子）的每一维特征均值都为0。因此投影到u上的样本点（仅仅有一个到原点的距离值）的均值仍然是0。

     回到上面左右图中的左图，我们要求的是最佳的u。使得投影后的样本点方差最大。

     因为投影后均值为0，因此方差为：

     

     中间那部分非常熟悉啊，不就是样本特征的协方差矩阵么（  的均值为0，一般协方差矩阵都除以m-1，这里用m）。

     用  来表示  ，  表示  ，那么上式写作

        

     因为u是单位向量，即  ，上式两边都左乘u得，

     即 

     We got it！

  就是  的特征值，u是特征向量。

最佳的投影直线是特征值  最大时相应的特征向量。其次是  第二大相应的特征向量，依次类推。

     因此，我们仅仅须要对协方差矩阵进行特征值分解。得到的前k大特征值相应的特征向量就是最佳的k维新特征，并且这k维新特征是正交的。得到前k个u以后，例子 通过下面变换能够得到新的样本。

     

     当中的第j维就是 PCA算法理解及代码实现

OpenCV小项目：自实现 Canny 算子

毕业设计/Matlab系列基于PCA和BP神经网络相结合的图像压缩技术

毕业设计/Matlab系列基于PCA的图像压缩算法实现（附matlab代码）

递归算法之阶乘代码实现与非递归实现

PCA算法（实现降维）