关联规则挖掘算法FP-Growth算法

Posted 2021-12-06 ZSYL

频繁项集挖掘-FP-Growth算法

• FP-Growth算法
• • FP-Growth原理分析
  • 算法实现

FP-Growth算法

FP-Growth（Frequent Patterns）相比于Apriori是一种更加有效的频繁项集挖掘算法，FP-Growth算法只需要对数据库进行两次扫描，而Apriori算法对于每次产生的候选项集都会扫描一次数据集来判断是否频繁，因此当数据量特别巨大，且扫描数据库的成本比较高时，FP-Growth的速度要比Apriori快。

但是FP-Growth只能用于发现频繁项集，不能用于发现关联规则。

FP-Growth原理分析

FP-Growth算法实现步骤

• 构建FP树
• 从FP树中挖掘频繁项集

FP-Growth算法将数据存储在一种被称为FP树的紧凑数据结构中。

下图就是利用上面的数据构建的一棵FP树（最小支持度为3）：

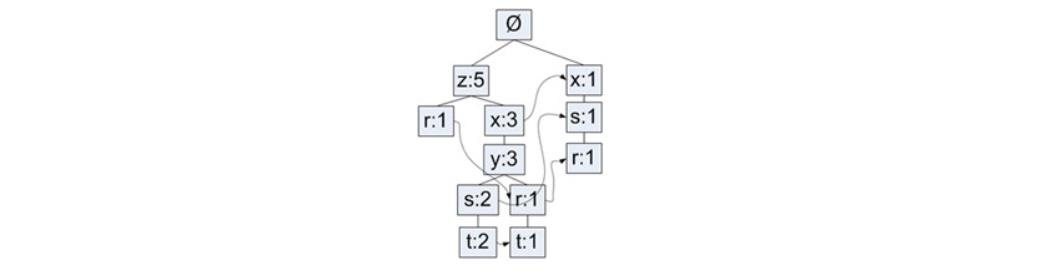
• FP树中最小支持度指项集总共出现的次数
• 一个元素项可以在一棵FP树中出现多次
• FP树存储项集的出现频率，且每个项集会以路径的方式存储在树中
• 存在相似元素的集合会共享树的一部分
• 只有当集合之间完全不同时，树才会分叉
• 树节点上给出集合中的单个元素及其在序列中的出现次数，路径会给出该序列的出现次数

FP-Growth算法工作流程：

• 扫描数据集两遍
• 第一遍对所有元素项的出现次数进行计数
• 根据前面的结论，如果某元素是不频繁的，那么包含该元素的超集也是不频繁的
• 第二遍扫描，只考虑那些频繁元素，并且第二遍扫描开始构建FP树

算法实现

class treeNode(object):
    def __init__(self, nameValue, numOccur, parentNode):
        # 节点名称
        self.name = nameValue
        # 节点计数
        self.count = numOccur
        # 记录相似的元素项
        self.nodeLink = None
        # 父节点对象
        self.parent = parentNode
        # 子节点
        self.children = {}

    def inc(self, numOccur):
        self.count += numOccur

    def disp(self, ind=1):
        print('--'*ind, self.name, ' ', self.count)
        for child in self.children.values():
            child.disp(ind+1)

def createTree(dataSet, minSup=1):  # create FP-tree from dataset but don't mine
    '''遍历数据集两遍'''
    # 第一遍对元素计数
    originHeaderTable = {}    # headerTable用于记录树的结构情况
    for trans in dataSet:
        for item in trans:
            originHeaderTable[item] = originHeaderTable.get(item, 0) + dataSet[trans]

    popKeys = []
    # 过滤掉非频繁项集
    for k in originHeaderTable.keys():
        # 记录非频繁项
        if originHeaderTable[k] < minSup:
            popKeys.append(k)

    freqItemSet = set(originHeaderTable.keys()) - set(popKeys)

    # headerTable用于记录树的结构情况
    headerTable = {}
    if len(freqItemSet) == 0:   # 如果初选没有频繁项集，那么直接退出
        return None, None

    # 重新构建headerTable
    for k in freqItemSet:
        headerTable[k] = [originHeaderTable[k], None]  # reformat headerTable to use Node link
    del originHeaderTable

    # 构建空树，根节点为空集
    root_node = treeNode('Null Set', 1, None)
    # 第二遍扫描，开始构建FP树
    for tranSet, count in dataSet.items():  # go through dataset 2nd time
        localD = {}
        for item in tranSet:  # put transaction items in order
            if item in freqItemSet:
                localD[item] = headerTable[item][0]
        if len(localD) > 0:
            orderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: p[1], reverse=True)]
            updateTree(orderedItems, root_node, headerTable, count)  # populate tree with ordered freq itemset
    return root_node, headerTable  # return tree and header table

def updateTree(items, parentNode, headerTable, count):
    # 判断第一个项集是已经是当前节点的子节点
    if items[0] in parentNode.children:  # check if orderedItems[0] in retTree.children
        # 如果是，那么直接count + 1
        parentNode.children[items[0]].inc(count)  # incrament count
    else:  # add items[0] to inTree.children
        # 如果不是，那么新建节点，并存储为当前节点的子节点
        parentNode.children[items[0]] = treeNode(items[0], count, parentNode)
        # 更新headerTable

        # 判断当前item是否是第一次记录
        if headerTable[items[0]][1] == None:
            # 如果是第一次，那么把新建的节点直接记录到头表中
            headerTable[items[0]][1] = parentNode.children[items[0]]
        else:
            # 如果不是第一次，那么说明新节点是当前item的节点的子节点，因此将它记录到当前分支的末位去，即设置为当前分支的叶子节点
            updateHeader(headerTable[items[0]][1], parentNode.children[items[0]])
    # 如果还有第二个元素，那么递归执行以上操作
    if len(items) > 1:
        updateTree(items[1::], parentNode.children[items[0]], headerTable, count)

def updateHeader(lastNode, newLeafNode):
    # 判断上一节点是否有连接节点，如果没有，那么说明上一节点就是叶子节点，那么直接将新节点设为叶子节点
    while (lastNode.nodeLink != None):
        # 如果上一节点已经有连接节点，那么循环知道遍历到叶子节点，再设置新叶子节点
        lastNode = lastNode.nodeLink
    # 将新的叶子节点设置为旧叶子节点的连接节点
    lastNode.nodeLink = newLeafNode


def loadTestDataset():
    dataset = [['r', 'z', 'h', 'j', 'p'],
               ['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],
               ['z'],
               ['r', 'x', 'n', 'o', 's'],
               ['y', 'r', 'x', 'z', 'q', 't', 'p'],
               ['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]
    return dataset

def createInitDataset(dataSet):
    dictDataset = {}
    for trans in dataSet:
        dictDataset[frozenset(trans)] = 1
    return dictDataset

def buildCombinedItems(leafNode, combinedItems):
    if leafNode.parent != None:
        combinedItems.append(leafNode.name)
        buildCombinedItems(leafNode.parent, combinedItems)

def buildCombinedDataset(nodeObject):
    # 根据节点名称，组合出新的项集节点
    combinedDataset = {}
    while nodeObject != None:
        combinedItems = []
        buildCombinedItems(nodeObject, combinedItems)
        if len(combinedItems) > 1:
            combinedDataset[frozenset(combinedItems[1:])] = nodeObject.count
        nodeObject = nodeObject.nodeLink
    return combinedDataset

def scanFPTree(headerTable, minSup, parentNodeNames, freqItemList):

    # 遍历排序后的headerTable，(节点名称，节点信息）
    for baseNode, nodeInfo in headerTable.items():
        # 根据prefix
        newFreqSet = parentNodeNames.copy()
        newFreqSet.add(baseNode)
        # 节点计数值
        nodeCount = nodeInfo[0]
        # 节点对象
        nodeObject = nodeInfo[1]
        # 记录下频繁项集以及计数
        freqItemList.append((newFreqSet, nodeCount))

        # 根据当前节点的子节点，构建出新的项集组合
        combinedDataset = buildCombinedDataset(nodeObject)

        # 根据新的项集组合，重合构建子FP树
        subFPTree, subFPTreeHeaderTable = createTree(combinedDataset, minSup)
        # 如果头表不为空，那么递归新树的头表
        if subFPTreeHeaderTable != None:
            print('conditional tree for: ', newFreqSet)
            subFPTree.disp(1)
            # 根据新的头表 扫描FP-Tree
            scanFPTree(subFPTreeHeaderTable, minSup, newFreqSet, freqItemList)

if __name__ == '__main__':

    from pprint import pprint
    simpDat = loadTestDataset()
    initSet = createInitDataset(simpDat)
    # 构建初始的FP-Tree
    initFPtree, initFPtreeHeaderTable = createTree(initSet, 3)
    initFPtree.disp(1)

    freqItems = []    # 存储频繁项集
    # 扫描FP树，找出所有符合条件的频繁项集

    root_node_names = set([])    # 从根路径空集开始扫描
    scanFPTree(initFPtreeHeaderTable, 3, root_node_names, freqItems)
    pprint(freqItems)