机器学习笔记：线性判别分析（Fisher）

Posted 2021-12-06 UQI-LIUWJ

        线性判别分析可用于处理二分类问题，其过程是寻找一个最佳的投影方向，使得样本点在该方向上的投影符合类内小、类间大的思想（“低耦合，高内聚”），具体指的是类内的方差之和小，类间的均值之差大。

1 、数据

        

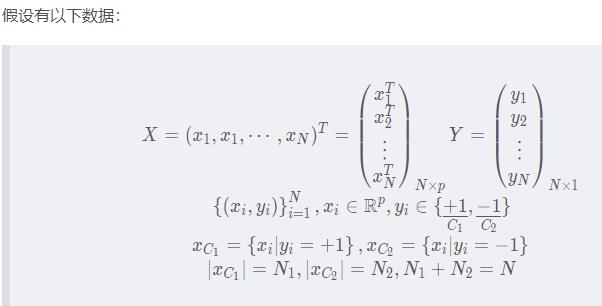
2 目标函数 

2.1 均值&方差

     ——>这个是两个类放到一块的数据集的均值和方差

     

   

 2.2 目标函数

 定义目标函数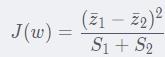

2.2.1 分子

分子是类间均值的距离（中心点之间的距离），越大表示类“分得越快” 

 

 2.2.2 分母

分母是两个类方差的和，越小表示每个类“内部越紧”

先看S1

S2 同理，所以有：

 2.2.3 目标函数整体

结合2.2.1和2.2.2，我们有：

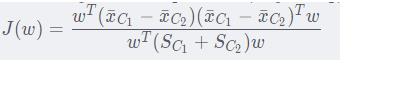
 极大化J(w)就可以使得类内的方差之和小，类间的均值之差大。

3 线性判别分析的求解

为了方便起见，我们令：

于是

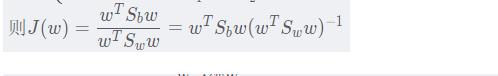
 对J(w)关于w求导数：

 

 参考内容：机器学习-白板推导系列笔记（四）-线性分类_scu-liu的博客-CSDN博客