机器学习之回归
Posted 长路漫漫,道阻且长
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习之回归相关的知识,希望对你有一定的参考价值。
近期阅读了《白话机器学习的数学》,为了将所读的内容充分理解消化,故将整理一系列文章,该篇是上一篇文章的续篇。
1.设置问题
基于广告费预测网站的点击量
2. 定义模型
- 假设点击量只与广告费这一个变量有关,现有一些数据(广告费与对应点击量的值),在坐标系中表示为下图
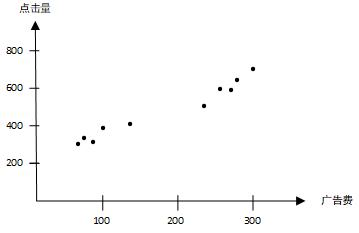
为了找出广告费与点击量之间的关系,可借助数学表达式即定义模型。为了方便,由上图建立广告费(x)与点击量(y)之间的函数关系为 f θ ( x ) = θ 0 + θ 1 x f_{\\theta}(x)=\\theta_{0}+\\theta_{1}x fθ(x)=θ0+θ1x即一次函数,这里的 f θ f_\\theta fθ 是指含有参数(变量)的函数,采用 θ 0 \\theta_0 θ0 和 θ 1 \\theta_1 θ1 代表变量,在机器学习中称为参数。一次函数的模型如下图:

机器学习中,变量或者预测值统称为参数。
3.如何求参
根据定义的模型求得的值与真实值存在一定的偏差,我们的目标就是使定义的模型求得的值尽可能贴近真实的值,也就是使模型的值与真实值的差值越来越小。
即为了求参,定义目标函数,然后微分求出参数的更新表达式。—这种算法也称为逻辑回归。
3.1 最小二乘法
最小二乘法就是目标函数为 E ( θ ) = 1 2 ∑ i = 1 n ( y ( i ) − f θ ( x ( i ) ) ) 2 E(\\theta)=\\frac{1}{2}\\sum_{i=1}^{n}(y^{(i)}-f_{\\theta}(x^{(i)}))^{2} E(θ)=21∑i=1n(y(i)−fθ(x(i)))2 ,通过不断修改参数的值,使得误差越来越小,。
Q1:误差怎么表示?
A1:按照设定的模型,由已知数据来求
θ
0
\\theta_0
θ0 和
θ
1
\\theta_1
θ1 。由于
f
θ
(
x
)
f_{\\theta}(x)
fθ(x) 求得的值与实际值是有误差的,我们的目标就是将模型求得的值接近真实值,即使所有数据的误差和降到最小。误差表示为:
E
(
θ
)
=
1
2
∑
i
=
1
n
(
y
(
i
)
−
f
θ
(
x
(
i
)
)
)
2
E(\\theta)=\\frac{1}{2}\\sum_{i=1}^{n}(y^{(i)}-f_{\\theta}(x^{(i)}))^{2}
E(θ)=21∑i=1n(y(i)−fθ(x(i)))2 ,
E
(
θ
)
E(\\theta)
E(θ)也称为目标函数,令其最小。其中
y
(
i
)
和
f
θ
(
x
(
i
)
)
y^{(i)} 和 f_{\\theta}(x^{(i)})
y(i)和fθ(x(i))不是指y和f的i次幂,而是指第i个数据对应的实际的值和模型计算的值。
Q2:为什么
E
(
θ
)
E(\\theta)
E(θ)是两者之差的平方而不是绝对值
A2:平方方便求微分(求导),而绝对值可能还需要对某些值的大小进行讨论
Q3:为什么需要乘
1
2
\\frac{1}{2}
21?
A3:结果导向,为了使最后的结果更加简单
为了求 E ( θ ) E(\\theta) E(θ)的最小值,对 E ( θ ) E(\\theta) E(θ)函数微分,以微分后的结果判断下一步 θ 0 \\theta_0 θ0和 θ 1 \\theta_1 θ1要调整的值,这里 x ( i ) x^{(i)} x(i)和 y ( i ) y^{(i)} y(i)为数据,值是已知的。
Q4:由微分结果如何调整参数的值?
A4:找到导数等于0的位置
最速下降法/梯度下降法
简单理解就是根据微分后的结果调整参数。
结合这个模型,
E
(
θ
)
E(\\theta)
E(θ)含有两个参数
θ
0
\\theta_0
θ0和
θ
1
\\theta_1
θ1,这里就用到偏微分(偏微分是对含有多个变量的表达式微分的方法,当对某一个变量微分时,其他的变量视为常量)。
若直接使用
E
(
θ
)
E(\\theta)
E(θ)对
θ
0
\\theta_0
θ0和
θ
1
\\theta_1
θ1偏微分,需要将
E
(
θ
)
E(\\theta)
E(θ)的表达式展开,很复杂,这里使用复合函数求偏微分。以下为具体过程:
令
u
=
E
(
θ
)
,
v
=
f
θ
(
x
)
ϑ
u
ϑ
θ
=
ϑ
u
ϑ
v
⋅
ϑ
v
ϑ
θ
令\\ u=E(\\theta),\\ v=f_\\theta(x) \\qquad \\frac{\\vartheta u}{\\vartheta \\theta}=\\frac{\\vartheta u}{\\vartheta v}·\\frac{\\vartheta v}{\\vartheta \\theta}
令 u=E(θ), v=fθ(x)ϑθϑu=ϑvϑu⋅ϑθϑv
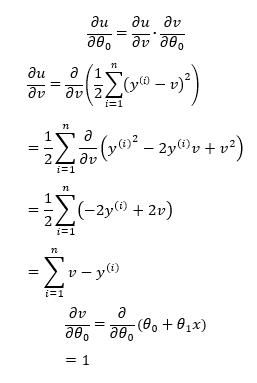
因此
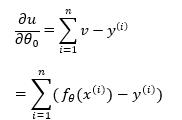
则
θ
0
\\theta_0
θ0的更新表达式为
θ
0
:
=
θ
0
−
η
∑
i
=
1
n
(
f
θ
(
x
(
i
)
)
−
y
(
i
)
)
\\theta_0 :=\\theta_0-\\eta\\sum_{i=1}^{n}(f_\\theta(x^{(i)})-y^{(i)})
θ0:=θ0−ηi=1∑n(fθ(x(i))−y(i))
同理可求得
θ
1
\\theta_1
θ1的更新表达式为
θ
1
:
=
θ
1
−
η
∑
i
=
1
n
(
f
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
(
i
)
\\theta_1:=\\theta_1-\\eta\\sum_{i=1}^{n}(f_\\theta(x^{(i)})-y^{(i)})x^{(i)}
θ1:=θ1−ηi=1∑n(fθ(x(i))−y(i))x以上是关于机器学习之回归的主要内容,如果未能解决你的问题,请参考以下文章