深度学习神经网络入门案例详细解析-鸢尾花案例
Posted 生产队的驴儿
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了深度学习神经网络入门案例详细解析-鸢尾花案例相关的知识,希望对你有一定的参考价值。
神经网络设计过程
案例: 鸢尾花分类
鸢尾花三种类别:
三种: 狗尾巴 杂草 小腹肌
 通过搭建一个神经网络来对鸢尾花进行分类
通过搭建一个神经网络来对鸢尾花进行分类
收集花朵 的特征值: 四种
花萼长
花萼宽
花瓣长
花瓣宽

以及:
三种输出结果
狗尾巴 杂草 小腹肌
操作方法:
1.收集数据集,花的特征,以及这些花是什么品种,即 标签。
2.将数据集 训练模型。通过反向传播训练。
3.将不知道品种的花的特征输入模型,自动出来花的种类。
神经网络模型:
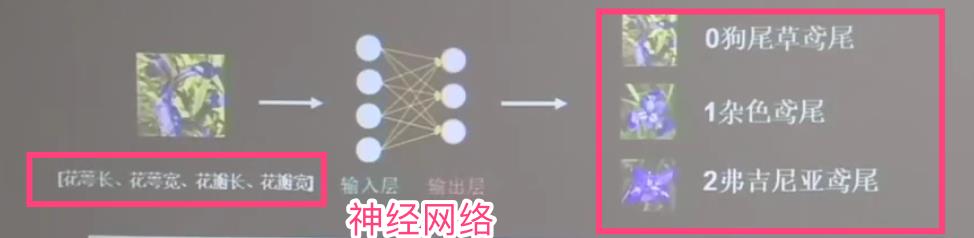
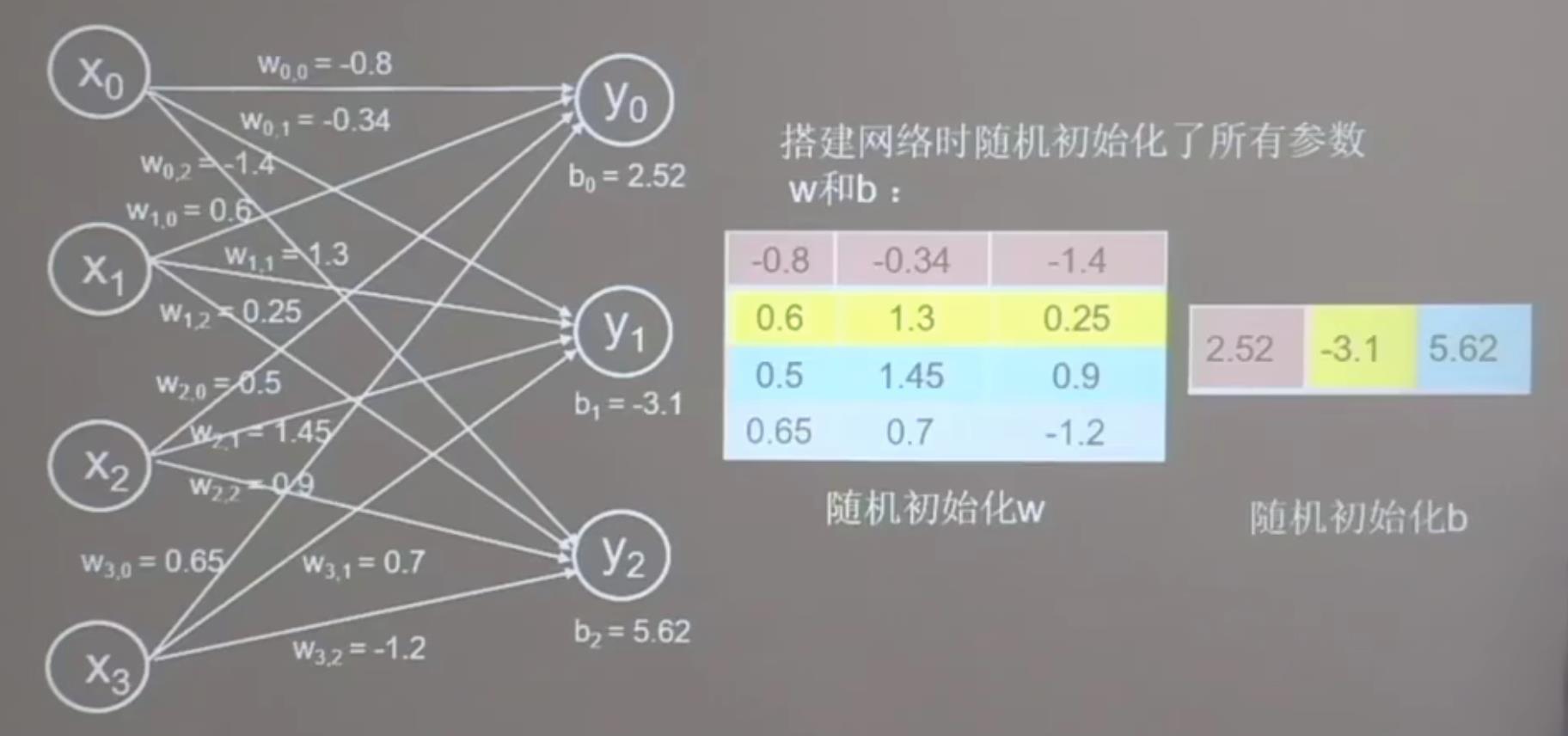
输入神经元 4个,输出神经元3个
4个是花的四个特征
3个是三种花
连接关系是12个,全连接,也成为全连接网络。
权重w和偏置b也会被随机分配初始化为0-1的数。
神经网络是由多个神经元组成的。
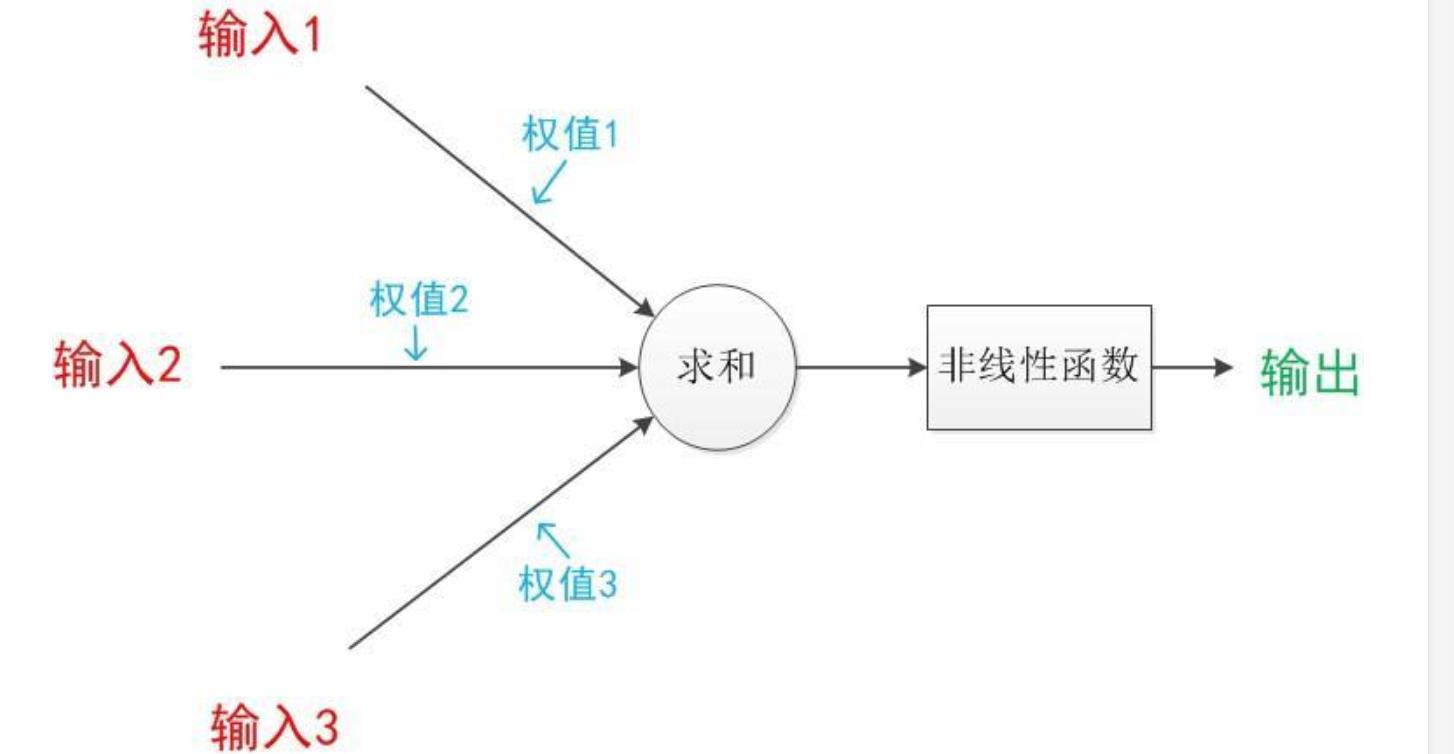
单个神经元结构图:
如下图,注意非线性函数也叫激活函数。
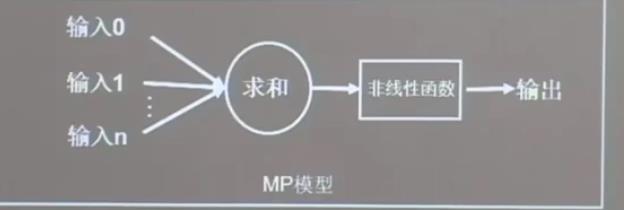
前面的输入到求和部分,细分为下图

前向传播:
代入训练集 的 x ,到模型里面,输出y的过程,称之为 前向传播。
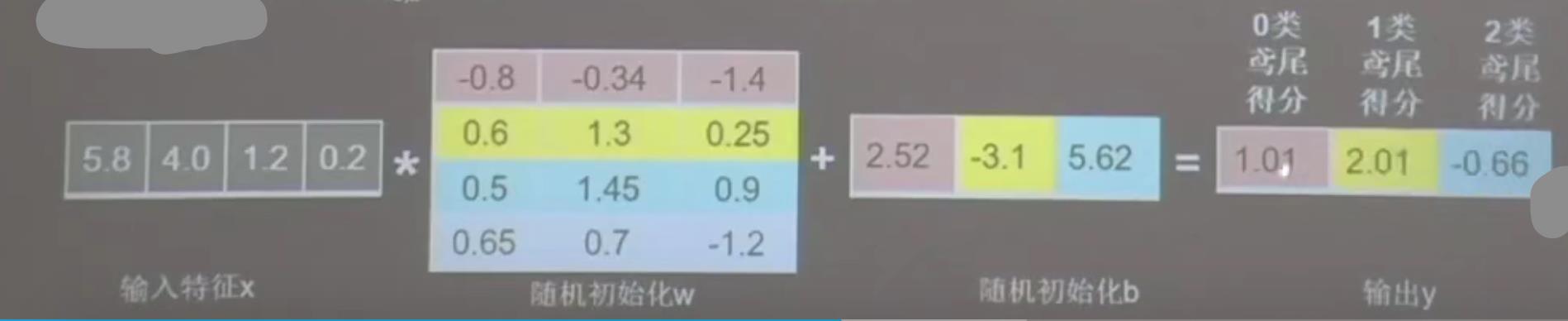
最初的参数w和b是随机产生的,所以,刚开始模型输出的结果很可能不对,是随便的。
但是要将模型输出的结果和真实值进行做差,平方求和,从而得到损失函数。
损失函数:
当损失函数最小,出现的w和b即为最优解。

损失函数有多个方式: 均方误差是最常见的。
因此,目的变成了 寻找一组w和b,让损失函数最小。
最常见的方法,即为 梯度下降法。
梯度下降法:

梯度下降法 还涉及 一个新的概念 叫做 学习率:
公式如下
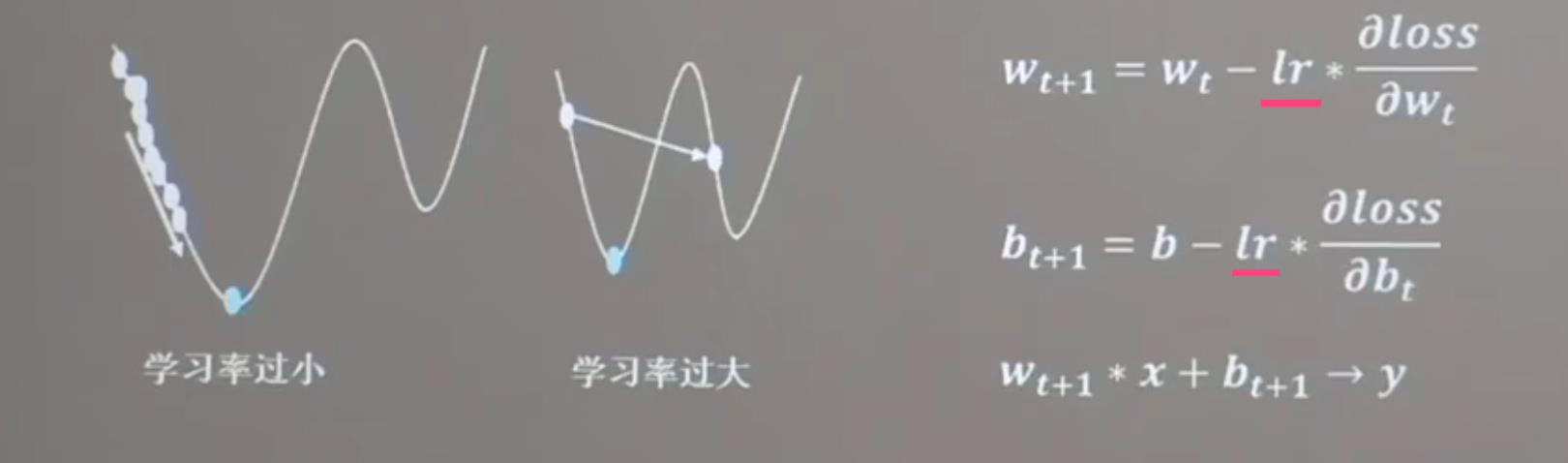
如果梯度下降比作,是从半山腰往下走的话。
学习率:就是下山的步幅长度。

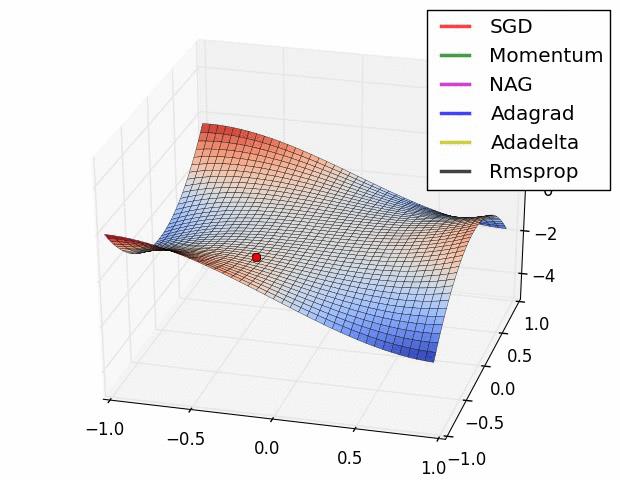
下面是一个经典的梯度下降示意图
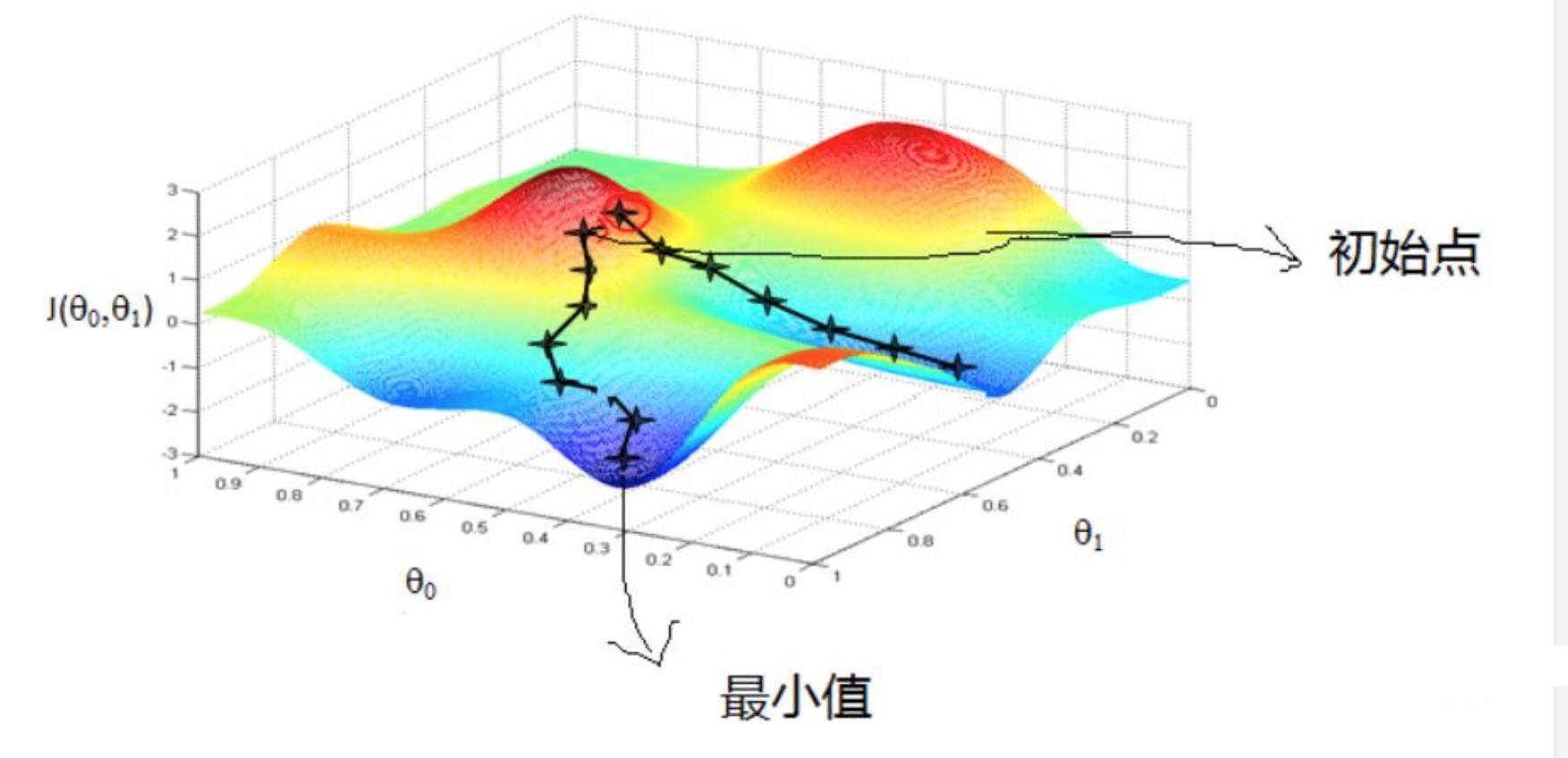
获取数据代码
from sklearn import datasets
from pandas import DataFrame
import pandas as pd
# .data返回iris数据集所有输入特征
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target
# .target返回iris数据集所有标签
# 为表格增加行索引(左侧)和列标签(上方)
x_data = DataFrame(x_data, columns=['花萼长度', '花萼宽度', '花瓣长度', '花瓣宽度'])
# 设置列名对齐
pd.set_option('display.unicode.east_asian_width', True)
# 新加一列,列标签为‘类别’,数据为y_data
x_data['类别'] = y_data
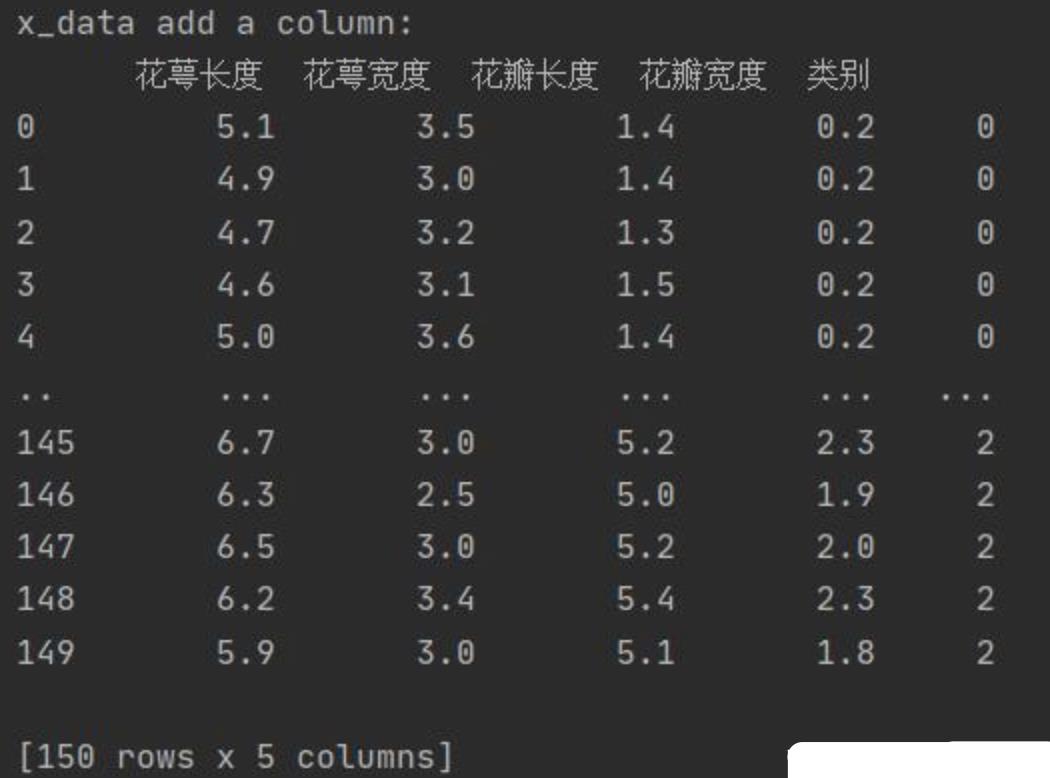
划分 训练集 和 测试集
训练集 训练模型
测试集 验证模型
一共150行数据:其中75%作为训练集,即120行;25%作为测试集,即后30行。
注意这里使用了seed随机种子函数,目的是为了在打乱x和y的同时,采用相同的随机数可以
保证其仍然是一一对应的关系。
之所以采用随机,是因为 模仿人的大脑,这里人在学习如何辨识花朵种类的时候,输入的也是无规律的数据。
# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
# 导入数据,分别为输入特征和标签
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target
# 随机打乱数据(因为原始数据是顺序的,顺序不打乱会影响准确率)
# seed: 随机数种子,是一个整数,当设置之后,每次生成的随机数都一样(为方便教学,以保每位同学结果一致)
np.random.seed(16) # 使用相同的seed,保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(16)
np.random.shuffle(y_data)
tf.random.set_seed(16)
# 将打乱后的数据集分割为训练集和测试集,训练集为前120行,测试集为后30行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]
# 转换x的数据类型,否则后面矩阵相乘时会因数据类型不一致报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)
# from_tensor_slices函数使输入特征和标签值一一对应。(把数据集分批次,每个批次batch组数据)
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)
batch
这里的bach
是为了训练更高效,通常会把数据变成batch(包),例如,把32行数据为一个小包batch。
这里一共有120个数据,32个数据打包为一个,分别是32,32,32,24.
最后一个包只有24个数据。
另外batch的选择参数,推荐,32,64,128等。选2的幂次方。
当然也可以选其他的数字。
tf.cast()是强制转换数据类型的函数
搭建神经网络
这里使用seed是为了确定每次生成的随机数是相同的,方便教学,实际情况可以删除seed=1
# 生成神经网络的参数,4个输入特征故,输入层为4个输入节点;因为3分类,故输出层为3个神经元
# 用tf.Variable()标记参数可训练
# 使用seed使每次生成的随机数相同(方便教学,使大家结果都一致,在现实使用时不写seed)
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))

设置超参数
# 学习率为0.1
lr = 0.1
# 循环500轮
# 这里的epoch是在对所有的训练数据,整体循环500次
# 一个epoch就是把所有训练数据丢进网络训练一次
epoch = 500 # 这里的epoch是在对所有的训练数据,整体循环500次
# batch_size是将多少个数据,扔进网络训练
batch_size = 10 # 是指扔进循环网络训练的数据是10个
train_loss_results = [] # 将每轮的loss记录在此列表中,为后续画loss曲线提供数据
test_acc = [] # 将每轮的acc记录在此列表中,为后续画acc曲线提供数据
loss_all = 0 # 每轮分4个step,loss_all记录四个step生成的4个loss的和
小tips:
epoch,batch_size和iteration区分
epoch:
当一个完整的数据集通过了神经网络一次并且返回了一次,这个过程称为一个 epoch。
因为
在神经网络中传递完整的数据集一次是不够的,而且我们需要将完整的数据集在同样的神经网络中传递多次。
我们使用一个迭代过程即梯度下降,优化学习过程和图示。
随着 epoch 数量增加,神经网络中的权重的更新次数也增加,曲线从欠拟合变得过拟合。
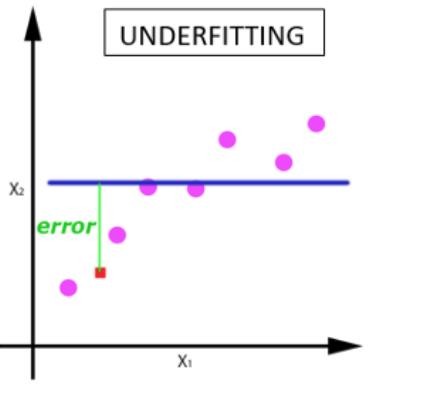
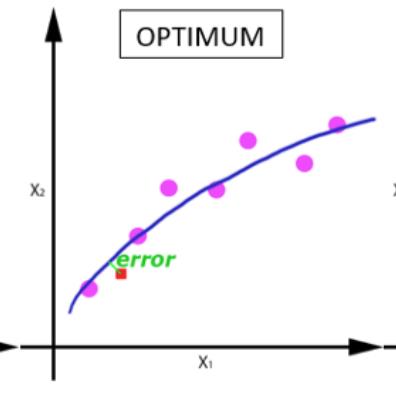
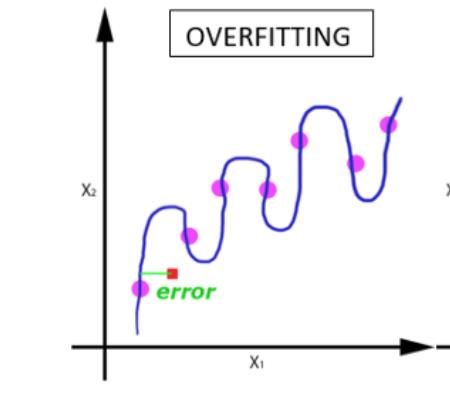
batch_size
在不能将数据一次性通过神经网络的时候,就需要将数据集分成几个 batch。
iteration 迭代次数
迭代是 batch 需要完成一个 epoch 的次数。
举个例子:总数据100个,batch_size为10个打一个包,迭代次数iteration就为10次。
一个有 2000 个训练样本的数据集。将 2000 个样本分成大小为 500 的 batch,那么完成一个 epoch 需要 4 个 iteration。
训练模型
通过 两层for循环更新参数,进行梯度下降,反向传播更新参数。
第一个for是针对将所有的数据,循环多少次。
这里训练集数据总共120个。epoch是500
意思是将这个120个数据,训练500次。
第二个for循环是针对包里面的数据进行循环,然后对权重w和偏置b求导数,进行梯度下降。
主要是32个数据,求一次真实值和模型输出之间的均方误差,然后修正w和b
for epoch in range(epoch): # 数据集别的 循环,每个epoch循环一次数据集
for step, (x_train, y_train) in enumerate(train_db): # batch级别 的循环
with tf.GradientTape() as tape: # with结构记录梯度信息
# 构建神经元
y = tf.matmul(x_train, w1) + b1 # 神经网络 乘加运算
y = tf.nn.softmax(y) # 使输出y符合概率分布(此操作后与独热码同量级,可相减求loss)
y_ = tf.one_hot(y_train, depth=3) # 将标签值转换为独热码格式,方便计算loss和accuracy
loss = tf.reduce_mean(tf.square(y_ - y)) # 采用均方误差损失函数mse = mean(sum(y-out)^2)
loss_all += loss.numpy() # 将每个step计算出的loss累加,为后续求loss平均值提供数据,这样计算的loss更准确
损失函数,需要一个包循环完毕之后,进行一次梯度下降的,同时更新一下w和b
32个数据一个包,一共120个数据,需要循环4次,才能完成一次大循环。
每进行1次32个数据的小循环,根据loss更新一下w和b,同时记录一下loss
# 根据损失函数计算梯度,进行梯度下降
grads = tape.gradient(loss, [w1, b1])
# 实现梯度更新 w1 = w1 - lr * w1_grad b = b - lr * b_grad
w1.assign_sub(lr * grads[0]) # 参数w1自更新
b1.assign_sub(lr * grads[1]) # 参数b自更新
# 每个epoch,打印loss信息
这里loss_all是把每个小循环的loss求和了,这里需要除以4,4个小循环一个大循环,来平均出,完成1次大循环
所下降的loss值
print("Epoch {}, loss: {}".format(epoch, loss_all/4))
测试部分,也要接在第一个for循环内,验证经过500次的整体大循环的情况下,acc和loss的变化曲线
total_correct = 0
total_number = 0
for x_test, y_test in test_db:
# 使用更新后的参数进行训练
y = tf.matmul(x_test, w1) + b1
y = tf.nn.softmax(y)
pred = tf.argmax(y, axis=1) # 返回y中最大值的索引,即预测的分类
pred = tf.cast(pred, dtype=y_test.dtype) # 调整数据类型和标签一致
# 如果预测值等于真实值,就输出为1,否则为0
correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
# 将每个batch的correct求和
correct = tf.reduce_sum(correct)
# 将batch中所有correct加起来求和
total_correct += int(correct)
# total_number为测试的总样本数,也就是x_test的行数,shape[0]返回变量的行数
total_number += x_test.shape[0]
# 总的准确率等于total_correct/total_number
acc = total_correct / total_number
test_acc.append(acc)
print("Test_acc:", acc)
print("--------------------------")
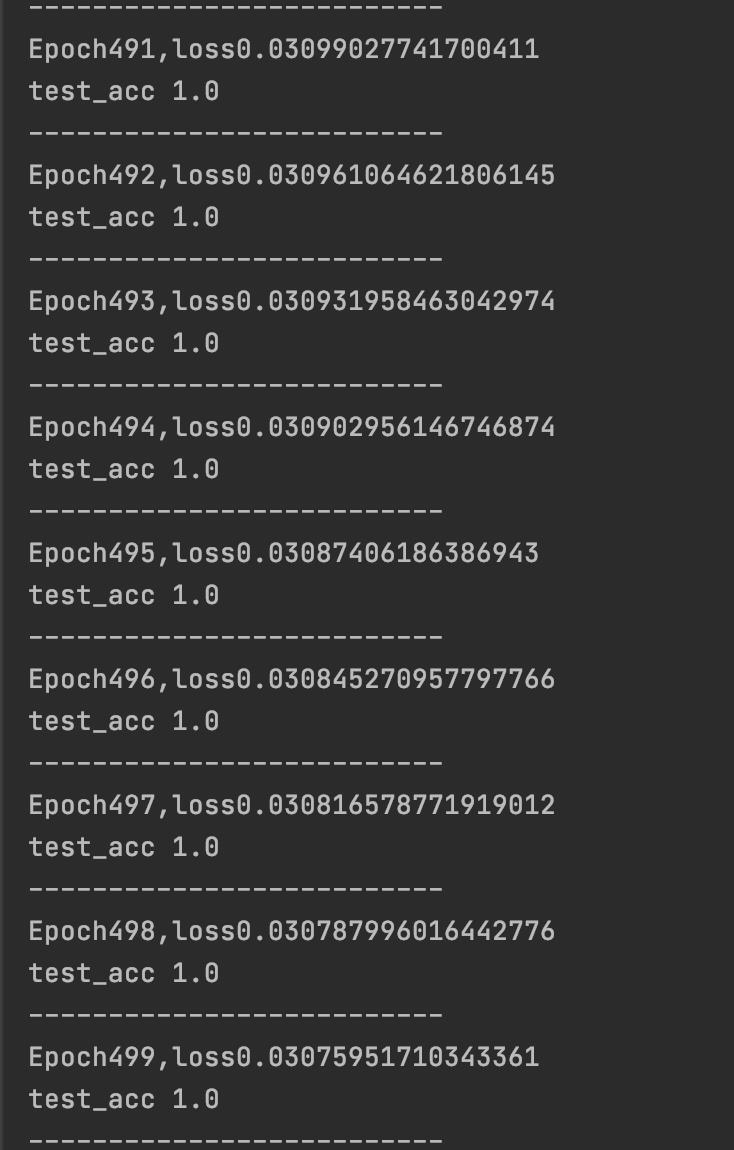
绘制loss和accuray曲线
# 绘制 loss 曲线
plt.title('Loss Function Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Loss') # y轴变量名称
plt.plot(train_loss_results, label="$Loss$") # 逐点画出trian_loss_results值并连线,连线图标是Loss
plt.legend() # 画出曲线图标
plt.show() # 画出图像
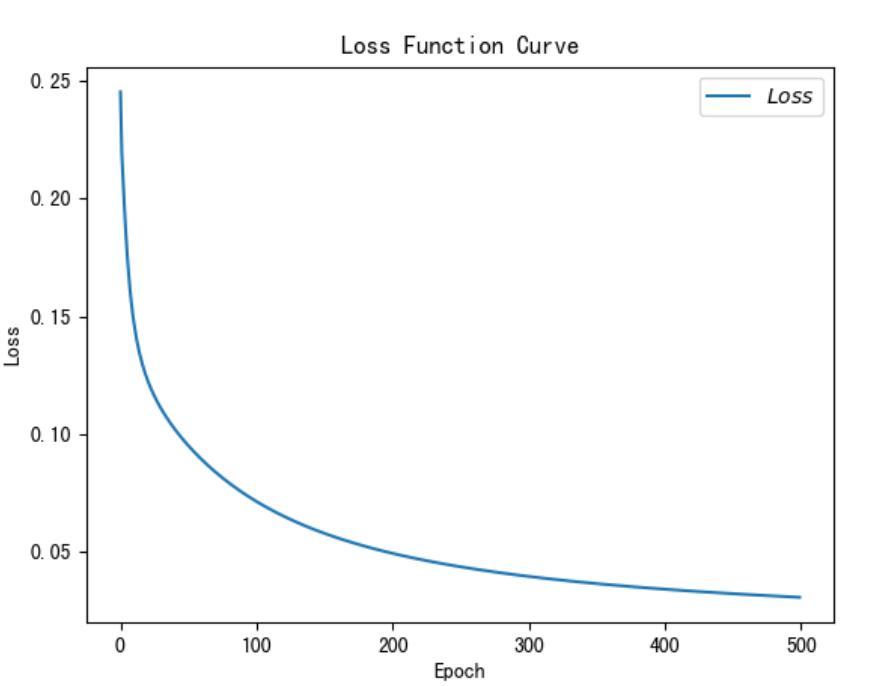
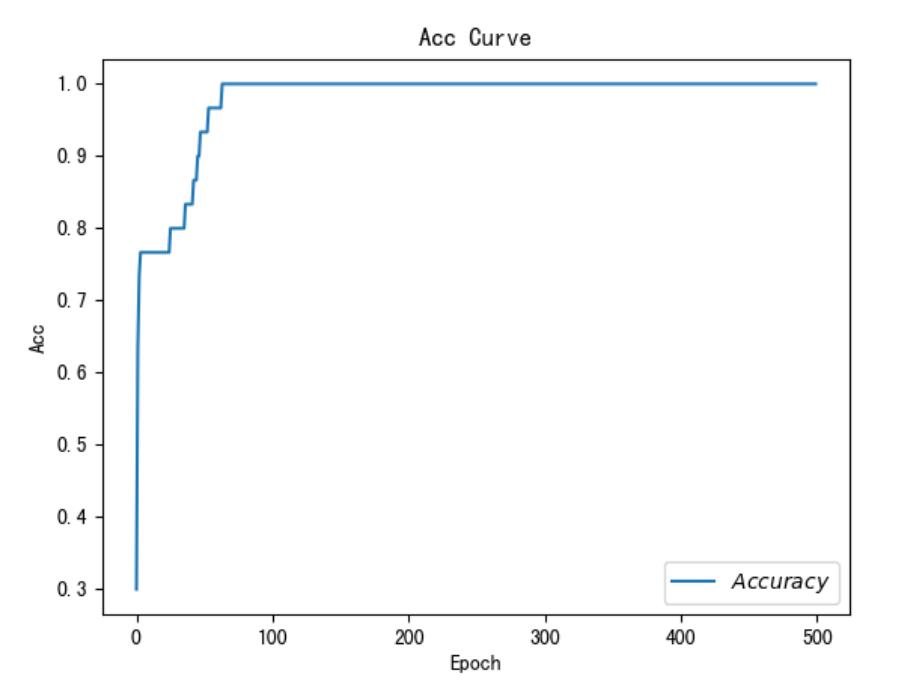
# 绘制 Accuracy 曲线
plt.title('Acc Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Acc') # y轴变量名称
plt.plot(test_acc, label="$Accuracy$") # 逐点画出test_acc值并连线,连线图标是Accuracy
plt.legend()
plt.show()
额外知识单独补充讲解
梯度下降的代码
import tensorflow as tf
# 初始化权重
w = tf.Variable(tf.constant(5, dtype=tf.float32))
# 设置学习率为0.2
lr = 0.2
# 设置迭代次数为40
epoch = 40
# 开始循环进行梯度下降,迭代40次,就是要执行40次下山
for epoch in range(epoch):
# 打开计算梯度的grads框架
with tf.GradientTape() as tape:
# 损失函数是 (w+1)的平方和
loss = tf.square(w + 1)
# 对损失函数中的w求偏导
grads = tape.gradient(loss, w)
# 根据求出的导数,进行反向传播,即w减少 导数*学习率
w.assign_sub(lr * grads)
# 打印出结果
print("After %s epoch, w is %f, loss is %f" % (epoch, w.numpy(), loss))
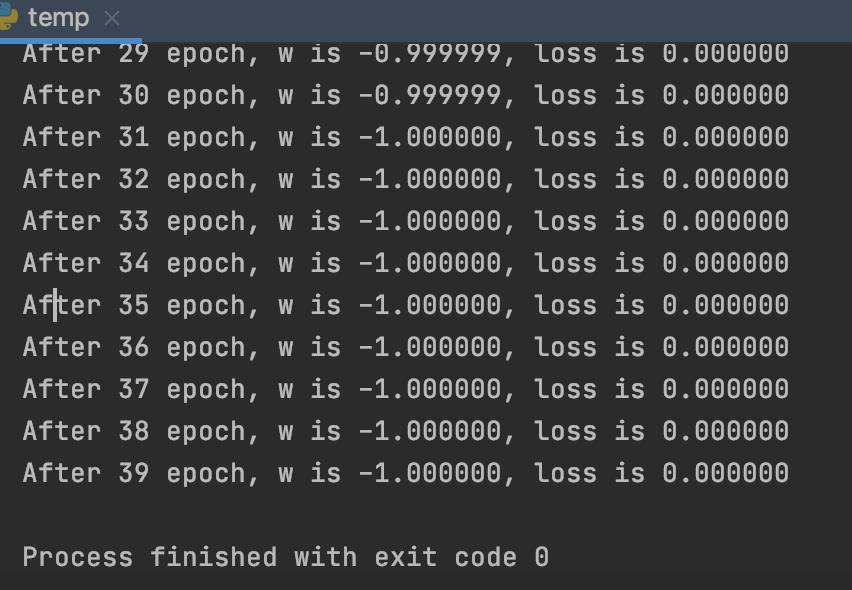
三步实现鸢尾花的分类
准备数据
搭建网络
参数优化

关于神经网络入门的一些知识整理
神经网络训练过程:
收集数据,整理数据
搭建神经网络,即 目标函数
真实值和目标函数值直接估计误差的损失函数
用损失函数值前向输入值求导
根据导数的反方向去更新网络参数(权重w和偏置b),目的是让损失函数值最终为0,最终生成模型
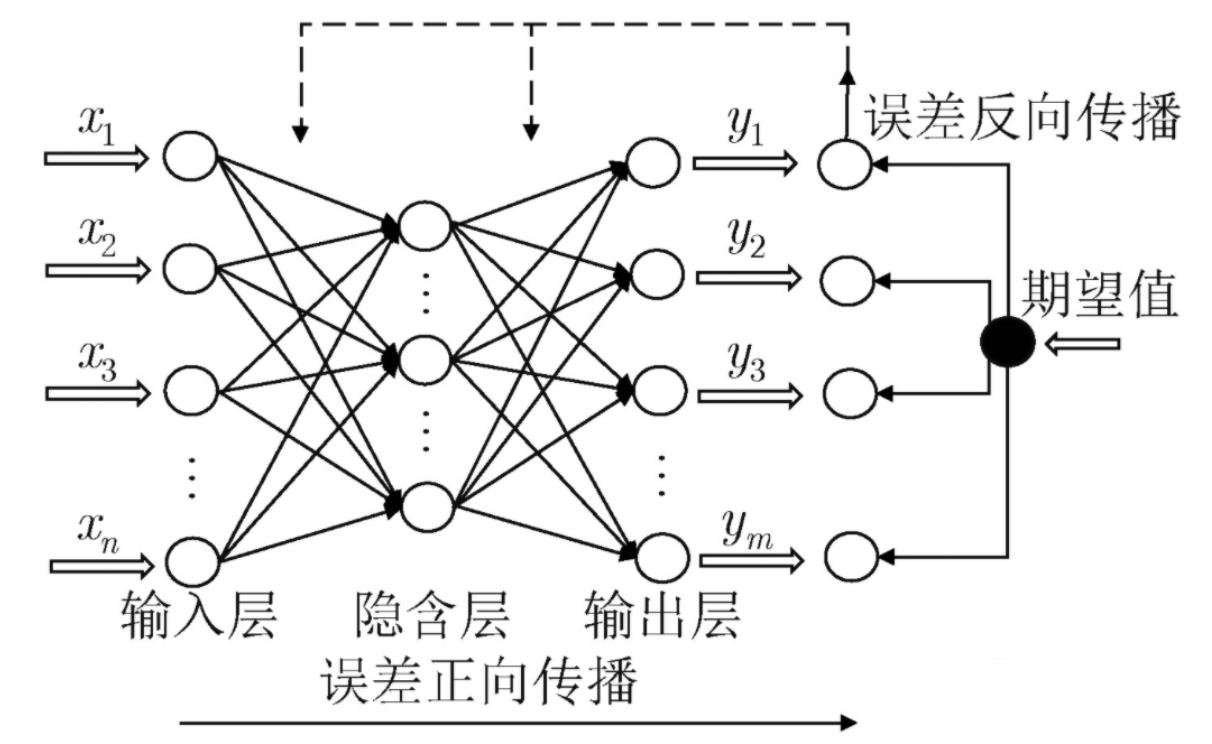
输入层:就是参数输入
输出层:就是最后的输出
隐藏层(隐含层):除去其他两层之外的层都可以叫隐藏层
模型包含两部分:神经网络结构,各个参数。
梯度:函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大。
前向传播:前向传播就是前向调用,就是把x代入到方程中,去求y值。
反向传播:反向传播就是根据误差和学习率,将参数权重进行调整。
数据预处理:
数据按比例缩放
归一化(normalization):将数据放缩到0~1区间,利用公式(x-min)/(max-min)。
标准化(Standardization):将数据转化为标准的正态分布,均值为0,方差为1。
正则化:正则化的主要作用是防止过拟合,
对模型添加正则化项可以限制模型的复杂度,使得模型在复杂度和性能达到平衡。
独热码编码 (one hot):
one hot编码是将类别变量转换为机器学习算法易于使用的一种形式的过程。one-hot通常用于特征的转换。
礼拜一,礼拜二,礼拜三,礼拜四,礼拜五,礼拜六,礼拜日。
写成 【 0 , 0, 3, 0, 0, 0, 0】
比如:一周七天,第三天可以编码为 [0,0,1,0,0,00]
数据处理库:
numpy ,pandas, matplotlib
numpy
优化版的python的列表,一般在使用的时候表示矩阵。
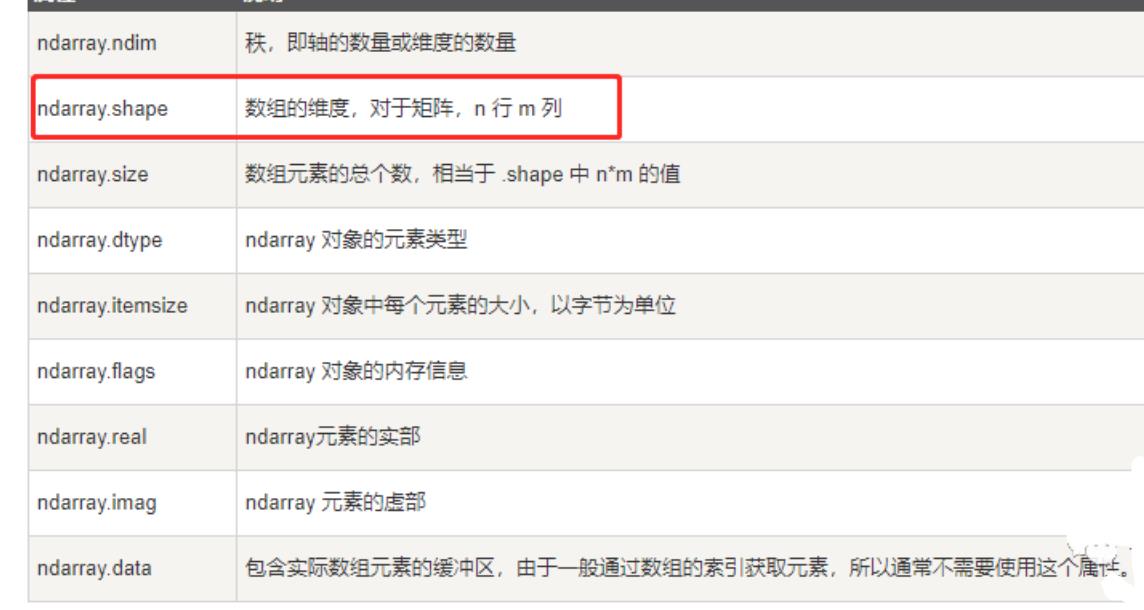
pandas
Pandas 的主要数据结构是 Series (一维数据)与 DataFrame(二维数据).
[Series] 是一种类似于一维数组的对象,它由一组数据(各种Numpy数据类型)以及一组与之相关的数据标签(即索引)组成。
DataFrame 是一个表格型的数据结构,它含有一组有序的列,每列可以是不同的值类型(数值、字符串、布尔型值)。DataFrame 既有行索引也有列索引,它可以被看做由 Series 组成的字典(共同用一个索引)。
matplotlib
画图用的,可以用来在学习的过程中对数据进行可视化,
训练集、测试集,测试集
训练集:用来训练模型的数据,用来学习的
验证集:用来验证模型的数据,主要是看下模型的训练情况
测试集: 训练完成之后,验证模型的数据
训练集-----------学生的课本;学生 根据课本里的内容来掌握知识。
验证集------------作业,通过作业可以知道 不同学生学习情况、进步的速度快慢。
测试集-----------考试,考的题是平常都没有见过,考察学生举一反三的能力。
损失函数
损失函数用来评价模型的预测值和真实值不一样的程度,损失函数越好,通常模型的性能越好。
f(x) 表示预测值,Y 表示真实值,

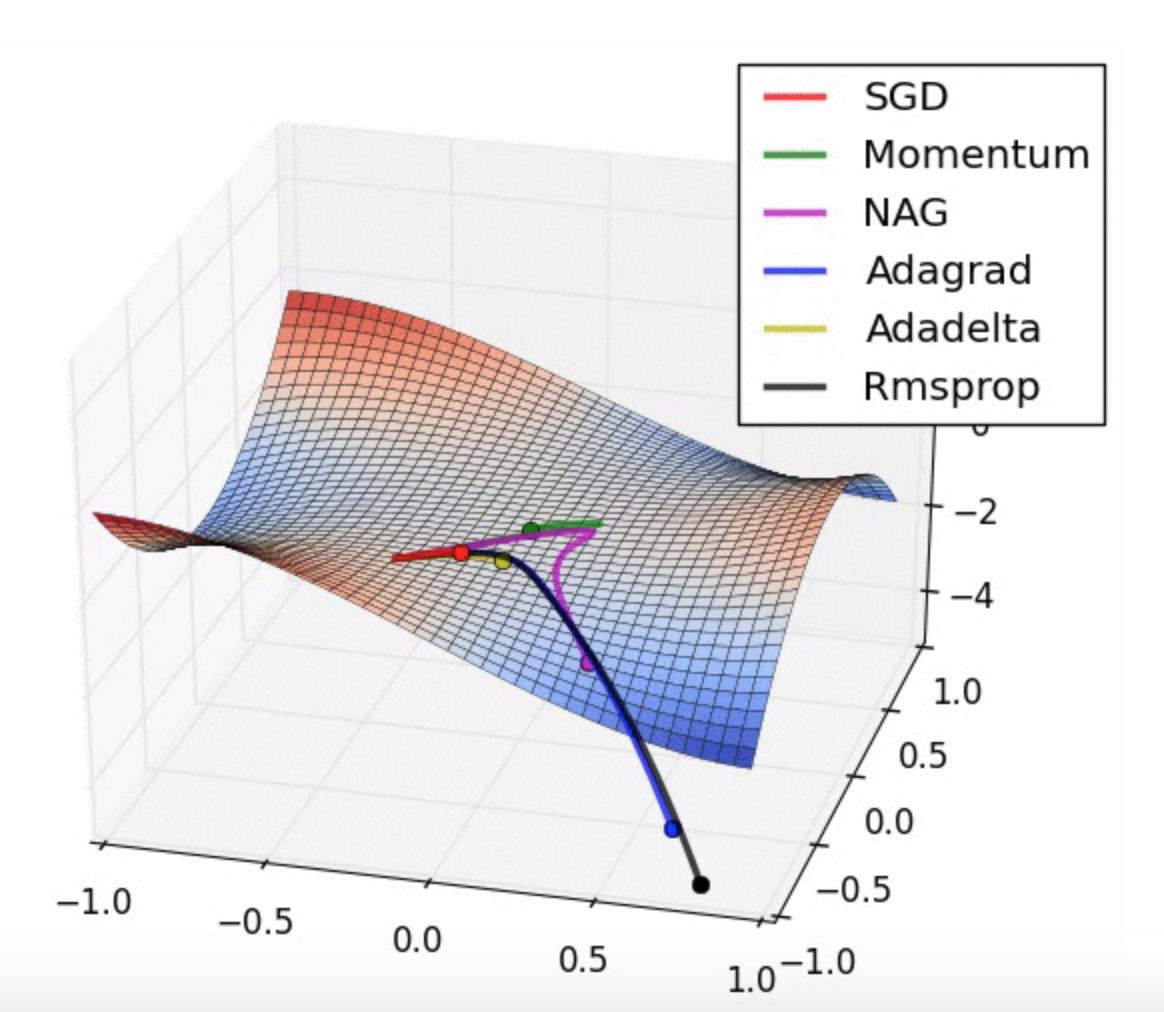
优化器
优化器就是在深度学习反向传播过程中,指引损失函数(目标函数)的各个参数往正确的方向更新合适的大小,使得更新后的各个参数让损失函数(目标函数)值不断逼近全局最小。
激活函数
激活函数就是对输入进行过滤,可以理解为一个过滤器
常见的非线性激活函数通常可以分为两类:
输入单个变量输出单个变量: sigmoid函数,Relu函数;
输入多个变量输出多个变量: 如Softmax函数,Maxout函数。
对于二分类问题,在输出层可以选择 sigmoid 函数。
对于多分类问题,在输出层可以选择 softmax 函数。
由于梯度消失问题,尽量sigmoid函数和tanh的使用。
tanh函数由于以0为中心,通常性能会比sigmoid函数好。
ReLU函数是一个通用的函数,一般在隐藏层都可以考虑使用。
有时候要适当对现有的激活函数稍作修改,以及考虑使用新发现的激活函数。
以上是关于深度学习神经网络入门案例详细解析-鸢尾花案例的主要内容,如果未能解决你的问题,请参考以下文章