5千字长文，深度总结HashMap底层实现&面试题收藏

Posted 飞人01_01

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了5千字长文，深度总结HashMap底层实现&面试题收藏相关的知识，希望对你有一定的参考价值。

哈喽，大家好！！！今天的主题：HashMap
反观整个Java的集合框架，我们讲了ArrayList、LinkedList、Stack、Queue、Deque、PriorityQueue等等集合，以及它们背后所对应的数据结构，今天我们来看一下java集合中，最为重要的，也是最常用的一个集合：HashMap。它的重要性，毋庸置疑，网上随意找一篇面经，几乎都会问到HashMap的底层实现、哈希冲突该怎么办？…… 这里我们就不细说了，直接进入主题。

文章目录

一、认识HashMap

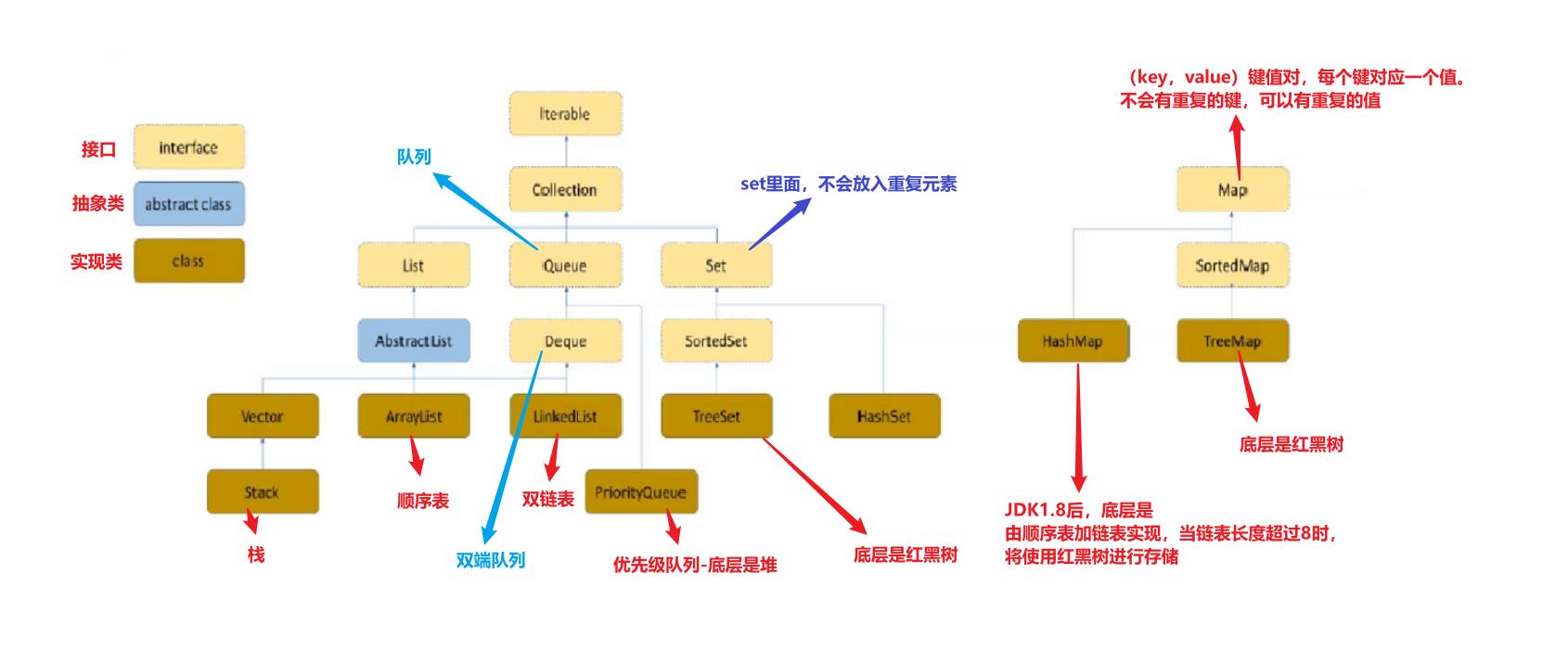
HashMap，实现了Map接口，数据存储形式采用键值对，也就是一个键对应一个值。如下图：

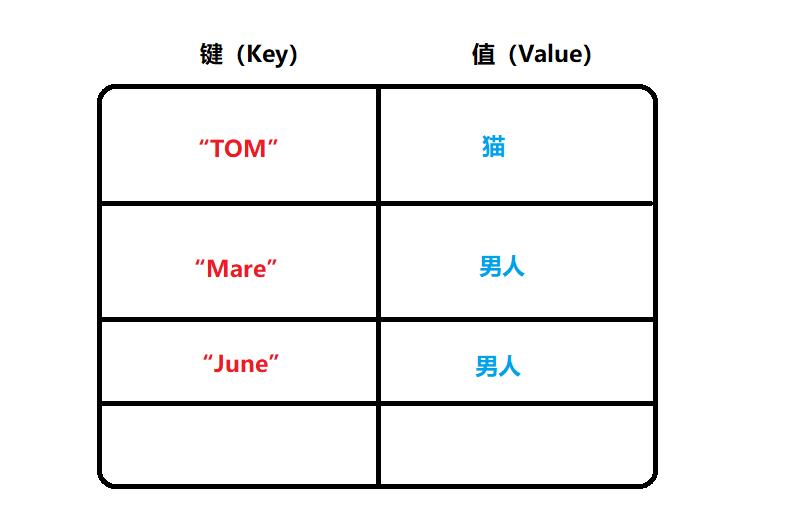
由上图可以清晰地看出，每一个键都对应一个唯一的值，并且键（Key）不能够重复，但值（Value）可以有重复的。这就是哈希表的形式，可能大家觉得这也没什么奇妙之处。不急，后面再说它的惊人之处。我们先来看看这该怎么使用这个HashMap。

构造方法：

HashMap<String, String> map1 = new HashMap<>(); //无参构造
HashMap<String, String> map2 = new HashMap<>(20);//指定初始容量
HashMap<String, String> map3 = new HashMap<>(20, 0.75f); //指定初始容量和负载因子

具体的用法就是：

  • 添加元素

    map1.put("TOM", "猫");//put方法，往里面添加元素

  • 获得值（Value）

    //根据TOM这个键，拿到相应的值。如果没有这个键，则返回null
String value = map1.get("TOM");

  • 删除元素

    map1.remove("TOM");//根据键，去删除键值对
map1.clear(); //删除map1的所有元素

  • 元素个数

    int size = map1.size(); //返回当前集合中的键值对数量

  • 查找是否包含键（Key）

    //查找map1是否有TOM这个键（Key）
boolean isContainsK = map1.containsKey("TOM");

  • 查找是否包含值（Value）

    //查找map1是否有猫，这个值（Value）
boolean isContainsV = map1.containsValue("猫");

  • map转Set

    //将map集合，转换为Set类型的集合
Set<Map.Entry<String, String>> entry = map1.entrySet();

以上方法，都好理解，主要就是最后一个Map转为Set的这个方法，我们讲解一下。

因为Set集合，它只是存储一个类型的元素，而不像HashMap这样是键值对。所有当HashMap转为Set时，会将HashMap的键和值，打包成一个整体（Map.Entry<K,V>）,打包后的对象类型就是这个括号里面的。然后再将打包好的整体放入Set集合中，如下图所示：

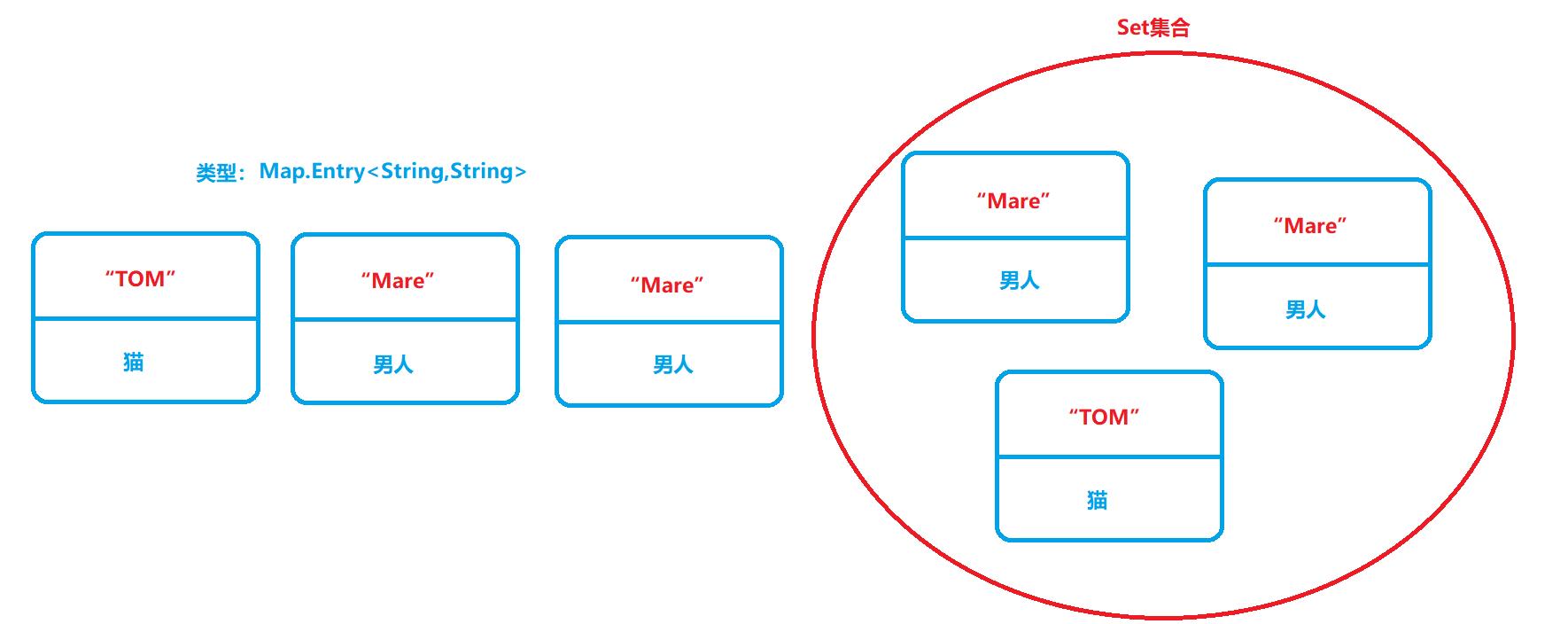
就如上图，打包成Map.Entry<K,V>类型，再放入Set集合中。这样做的好处就是，可以使用迭代器（Iterator）进行遍历，因为Map接口是没实现Interable接口的，无法使用迭代器，只能转为Set集合，再使用迭代器。以下是使用迭代器的代码：

Set<Map.Entry<String, String>> entry = map1.entrySet();
for (Map.Entry<String,String> set : entry) {
    //调用get方法，即可拿到键和值
    String key = set.getKey();
    String value = set.getValue(); 
}

还有值得注意的是，键重复的情况，假设目前HashMap中已经有了（“TOM”，“猫”）这一对键值。如果此时我再添加元素（“TOM”，“狗”），因为键是一样的，则会找到表中TOM的位置，将“狗”放入了表中，实现了覆盖的效果。如下代码：

HashMap<String,String> map1 = new HashMap<>();
map1.put("TOM", "猫"); //第一次放入
map1.put("TOM", "狗"); //第二次方法，则会将猫改写为狗

二、哈希函数

1、哈希函数的概念

在我们前面学习的所有数据结构中，无论是二叉树，还是链表，在增删查改的操作上，时间复杂度都还是有那么一点点不尽人意，拿搜索二叉树举例，当插入的数据有序时，会退化成链表，从而产生了平衡树。但平衡树的增删查改也只能做到O（logN）的水平，没法再快了。

但哈希函数可以做到O(1)的水平，这是一个非常恐怖的概念，增删查改都能做到O(1)的水平，快了不止多少倍。那么它到底是怎么实现的？我们来简单分析一下：

哈希函数：根据给定的数据，进行计算，得到一个地址，在这个地址的地方进行放入元素。

取出元素的时候，也只是根据数据计算一个地址，在该地址处取出元素。

这就是哈希函数简单的认识。就是根据一些计算，推导出一个地址。

比如：hash = 元素 % 10; 这样一个最简单的哈希函数公式，假设我们传递的数据,是99，则99 % 10 = 9。则在数组下标为9的位置放入数据……

但是还有一个问题就是：假设现在传递的数据是89，89 % 10 = 9。还是在下标为9 的位置进行插入数据。此时就发生了意外，当前9下标位置已经有数据了。

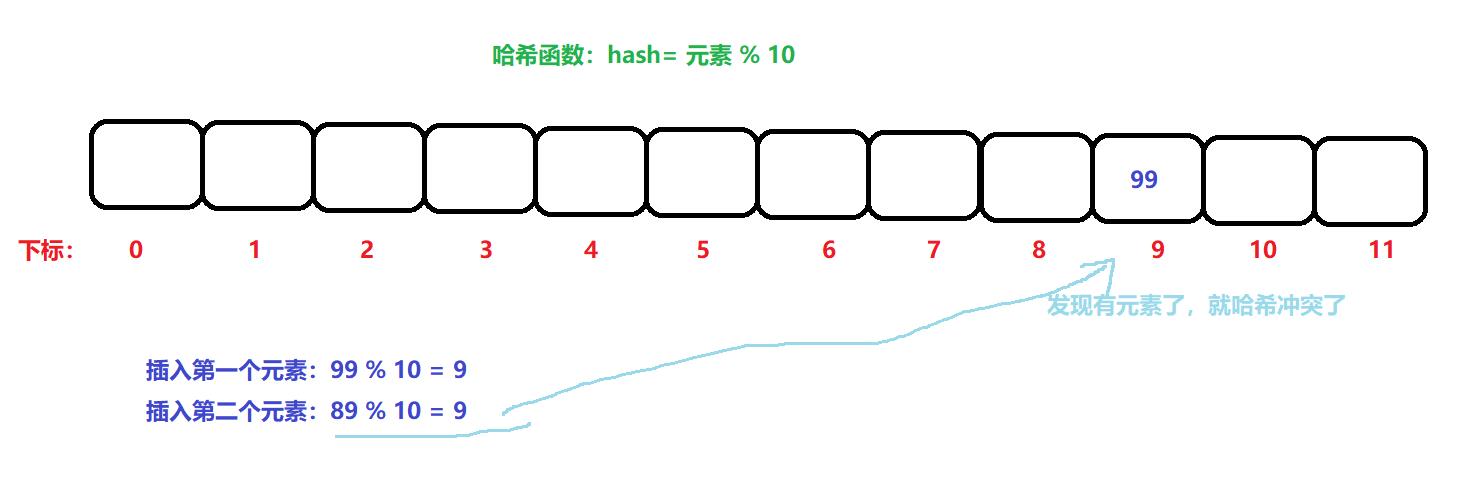
以上这样的情况，就称为哈希冲突。不同的关键字，根据相同的哈希函数计算出相同的哈希值，就是哈希冲突。

人们可以设计出精妙的哈希函数，来降低哈希冲突的概率，但是绝对不可能做到不发生冲突。也就是说，但我们添加元素足够多时，发生哈希冲突，是一个必然的现象。

常见的哈希函数，我们这里就不列举了，大家查一下就行。大多数人都不会去设计哈希函数，我们只需知道有这么个东西即可。

2、哈希冲突，该怎么办？

为了尽量降低哈希冲突，我们就得从两个方面着手：在发生冲突之前和发生冲突之后。

发生冲突之前：设计出精妙的哈希函数，存放数据的内存空间开辟大一点，还有就是有一个负载因子的概念。

负载因子：

也就是表中的元素除以哈希表的长度，就是负载因子。

负载因子的曲线图大致如下：

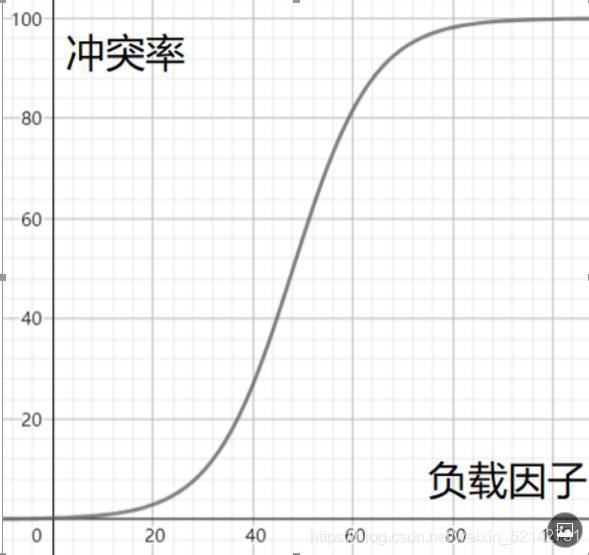
也就是说在负载因子达到一个界限的时候，就需要进行扩容，将数组扩大，即可降低负载因子。

以上方案只是在尽量预防发生冲突，那如果真的发生冲突了，又该怎么办？

哈希冲突后：

常见的解决哈希冲突的方法是：闭散列和开散列。

闭散列：也叫开放地址法，当发生哈希冲突的时候，说明此当前下标位置已经有数据了，此时我们只需沿着当前位置往下查找一个没放数据的位置，插入数据即可，如下：

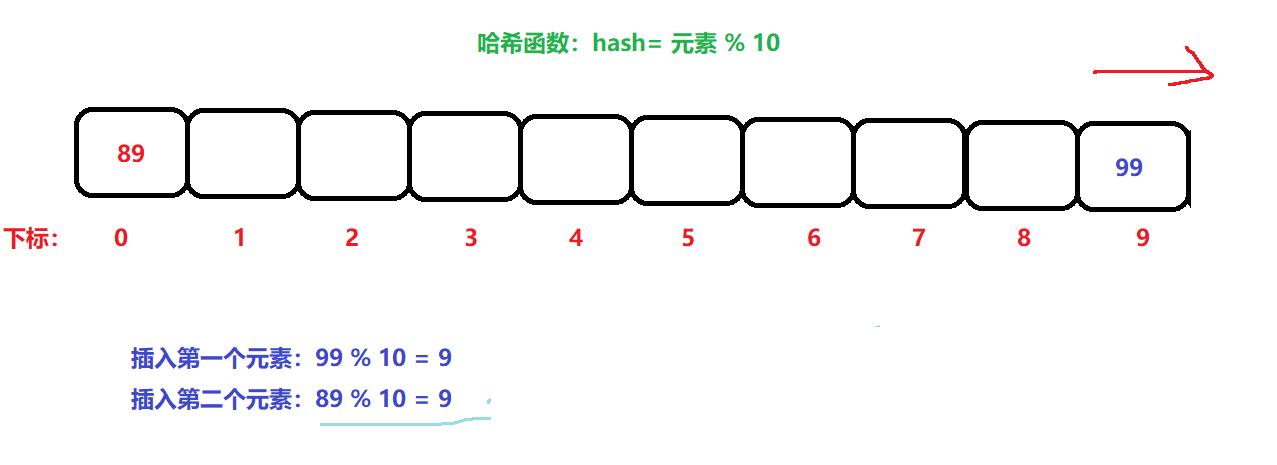
在插入89时，发生了冲突，就在9下标的后面找到一个空位置插入数据，但是9下标后面没位置了，则从数组前面开始找。

那有人可能就会问，会不会整个数据都已经满了呢？？

不可能的！因为有一个负载因子在控制数组的大小，当负载因子达到一个值的时候，就会进行扩容。

以上的方法就称为线型探测法。沿着下标，一直往下找，找到一个空位就插入即可。但是这样做的不好之处就在于，发生冲突的所有数据都聚集在一块地方，对删除操作增加了不小的难度。

例如：假设现在需要删除99，那能直接将99拿走吗？如果拿走了，那89，又如何通过哈希函数取出呢？？

所有线型探测法，对于删除操作，采用了伪删除法，也就是说，有一个变量记录99的状态表示已经删除了。

除了线型探测，还有二次探测法，就是为了解决冲突的元素聚集在一块这个问题：二次探测法，将不在沿着冲突位置的下标一个一个往下找空位置，而是通过一个公式：待插入下标 = （冲突下标 + i 2）% m 。此处的i就是发生冲突的次数。比如89第一次插入时，会跟99第一次发生冲突，计算下一个下标后，发现下一位置还是冲突的，则i=2，一直往下推导……

最重要的就是开散列：

开散列：又叫链地址法。将发生冲突的元素，用一个单链表进行串连起来，将头节点，放入数组中即可。如下图：

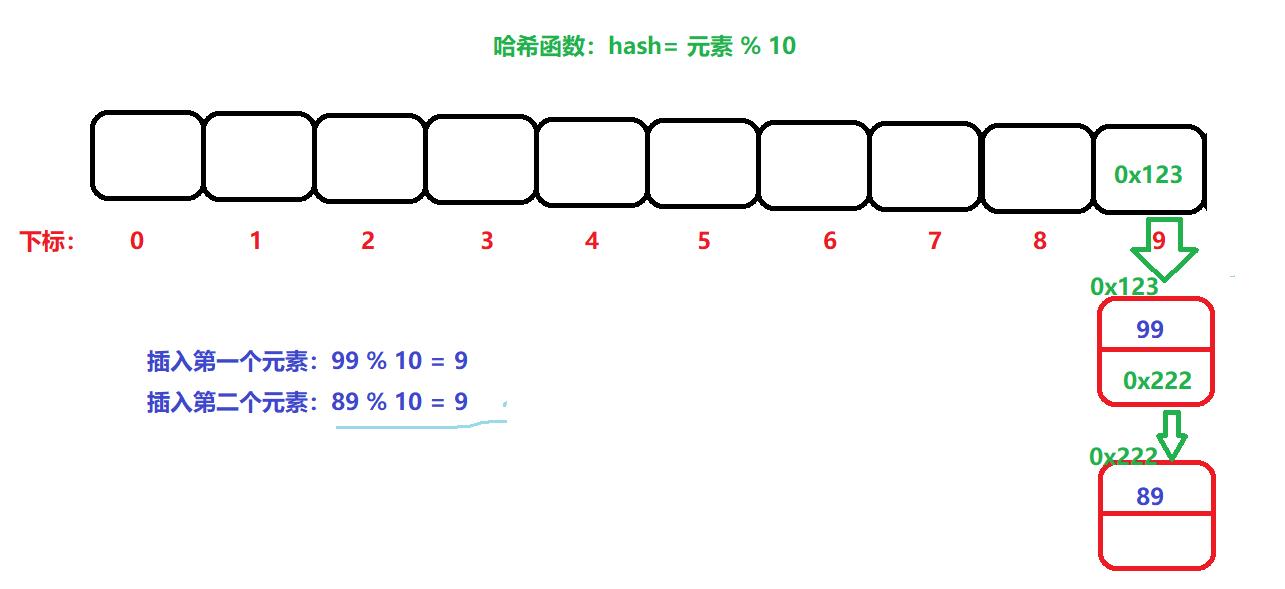
将所有发生冲突的元素，用一个单链表串连起来即可。然后在这个单链表中一个个查找。

但是还是会出现意外，如果单链表的长度很长的话，还是做不到O(1)的时间复杂度，那么此时就需要将这个单链表，转换为一个哈希表，或者是建一个红黑树（JDK1.8之后）的形式。

以上两种方法，就是解决哈希冲突之后的方案，特别值得记住的就是开散列。

3、JDK1.8的HashMap源码

（1）构造方法

在JDK1.8之前，HashMap只是采用数组+单链表的形式进行存储，且当时的单链表是用头插法的形式插入节点的。

在JDK1.8之后，HashMap采用数组+单链表+红黑树的形式进行存储，且单链表是用尾插法的形式插入节点。

那么是怎么进行存储的，我们来简单分析一下源码：

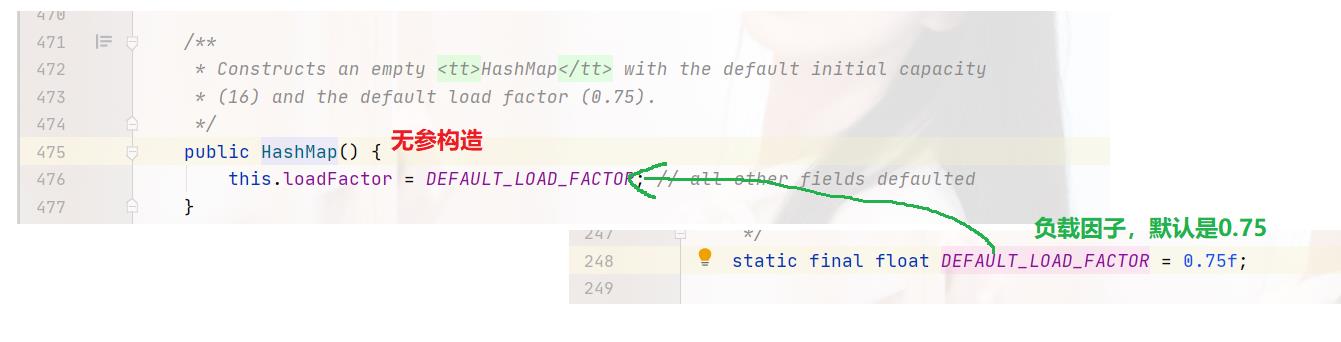
无参构造方法，只是设置了负载因子，并没有设置HashMap底层数组的大小。所以，只调用构造方法，不调用put方法，数组大小是0。跟ArrayList是一样的，ArrayList在调用add时，会将数组大小设置为10。

有参构造方法：

切记：HashMap底层数组的大小，一定是2的某次方，假设调用方传递的是20，这个数并不是2的某次方，则会向上调整，取离20最近的，且还是2的某次方的数。这里的话，离20最近且还是2的某次方的数，就是32。

千万注意，HashMap底层数组大小，不一定就是new的时候的初始化容量。

其次，我们需要认识一下几个常见的成员变量，以便于我们后续读懂put方法。

（2）put方法

在读put方法前，一定需要理解上图中的几个成员变量的意义，然后再来读put方法，这样才不至于越看越懵。

  1. 首先第一步就是put方法，调用了putVal方法 。这里需注意hash函数，设计的比较精妙。

    hash函数，除了调用了hashCode方法以外，还将计算出来的hashCode的值右移了16位，然后再做与运算。因为hashCode放回的是int类型，右移16位是将这个数值的每一位都利用起来。

  2. putVal方法

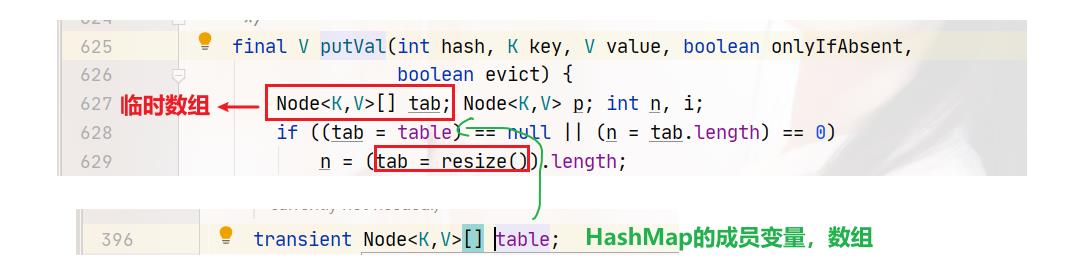
    tab指向成员变量table数组，n就是当前数组的长度。

    首先我们先来看第一条逻辑分支，628行。tab=table，首先是判断是否为null，第二判断就是数组的长度等于0的时候。当调用无参构造方法时，没有为数组分配大小和赋值等操作，所有此时调用put方法是，第628行的逻辑判断就是真：

    第629行，tab=resize（）。人如其名，resize就是调整数组大小的。这个方法有两个作用：初始化数组大小和扩容。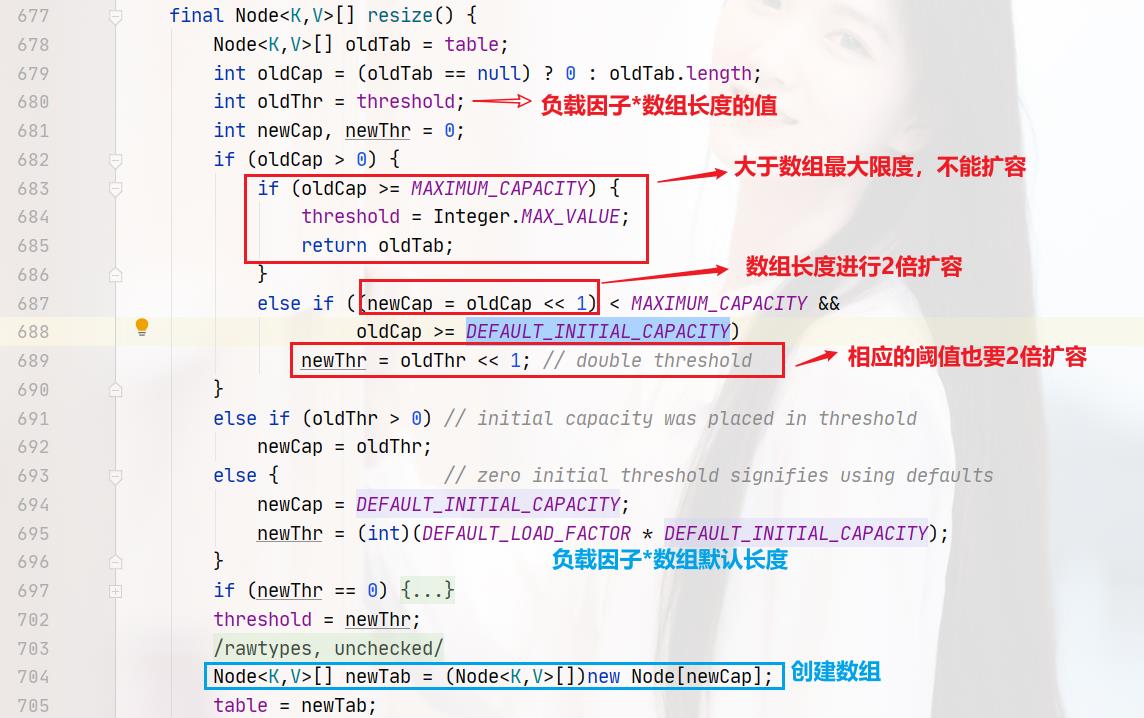

    677行至705行的代码，就是初始化创建table数组。706行至749行的代码，就是将扩容前的旧数组的所有数据重新进行hash计算，放入新数组，这里就不多讲了，代码如下：

  3. 数组开辟好之后，就是将Key和Value放入HashMap中

    切记切记：上图的蓝色框中，非常重要，可以说是精妙绝伦、无与伦比的设计理念。

    i = （n - 1）& hash。 n是当前数组的长度，假设就是16，hash就是Key计算出来的哈希值

    在n是2的某次方的前提下，切记切记，必须是2的某次方的前提，重要的事说三遍！！！

    在n是2的某次方的前提下，切记切记，必须是2的某次方的前提，重要的事说三遍！！！

    在n是2的某次方的前提下，切记切记，必须是2的某次方的前提，重要的事说三遍！！！

    i = (n - 1) & hash ，等价于 i = hash % n

    这一点非常非常重要！！！

    因为位运算肯定是比取模运算快，这也是为什么在前面讲构造方法的时候，JDK为什么会将容量调整为2的某次方的原因。可以说，JDK的实现者，为了加快HashMap的速度，费了大心思。

    这一点理解后，就好理解后面的了。根据上面的i计算之后，当前i的值肯定是在0~n-1的范围内。此时再去相应的位置放数据。

    第630行判断当前i位置是不是null，如果是null，说明这个位置还没有元素，直接插入node节点即可。

    不用想，632行开始，就是i位置不是null时，就需要将新节点插入到单链表中

    在调整为红黑树的时候，网上很多帖子写的都是在JDK1.8之后，当链表长度大于8时，就调整为红黑树，这是错的。

    调整为红黑树的代码如上图，如果此时的数值长度没有超过64时，只会进行扩容，不会调整为红黑树。

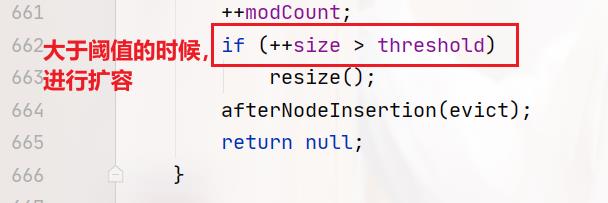
    代码的最后就是计算当前HashMap的元素个数，看是否超过了负载因子*数值长度，这个阈值。超过了就扩容：

三、面试题总结

  • 如果new HashMap（19），此时HashMap内的数组长度是多少？

    答：如果只是调用构造方法的话，数组大小是0。因为此时的构造方法，只是将计算好的数组长度存储到一个成员变量里，还并没有开辟数组，在第一次调用put方法时，会调用resize方法，进行开辟数组。 如果除了调用构造方法，还调用了一次put方法的话，那么数组长度就是32，因为JDK底层会将19向上调整，第一个是2的某次方的数，就是最后数组的长度。

  • 那么为什么JDK底层会调整19这个数组长度呢？必须是2的某次方，目的是什么？

    答：因为在存放数据的时候，需要对哈希值求余数，这个余数就是数组的下标。如果此时用取模运算（%），不够高效；而当数组的长度是2的某次方的时候，可以通过以下公式直接计算取模后的结果：i = (n - 1) & hash。（与运算比取模运算快）

  • HashMap在什么时候进行扩容？

    答：在JDK1.8中，当前哈希表的元素个数大于等于负载因子*数组长度时，会进行扩容操作。（JDK1.8的负载因子是0.75）

  • 当两个对象的hash值相同时，会发生什么？

    答：哈希冲突。

  • 如果两个键的hash值相同，该怎么取到相应的Value值？

    答：遍历当前的链表（红黑树），如果在某一个节点处，这个节点Key和此时我传递进去的Key相等，那么就是当前这个节点Value。

  • 你了解过重新调整HashMap大小时存在什么问题吗？

    答：重新调整HashMap的大小，会将以前旧数组的所有数据，重新进行哈希计算，再放入新数组。

  • HashMap的内部是如何进行存储数据的？

    答：在JDK1.8之前，采用数组+单链表的形式，且单链表的插入方式是头插法。在JDK1.8之后，采用数组+单链表+红黑树的形式，且单链表的插入方式是尾插法。

  • 在什么情况下，HashMap会将单链表转换为红黑树？

    答：在数组的长度大于等于64，且单链表的长度大于等于8的时候，会转换为红黑树。

好啦，本期更新就到此结束啦！！！我们下期见！！！

以上是关于5千字长文，深度总结HashMap底层实现&面试题收藏的主要内容，如果未能解决你的问题，请参考以下文章

C++之string的底层简单实现！（七千字长文详解）

5 千字长文+ 30 张图解 | 陪你手撕 STL 空间配置器源码

万字长文|Hashtable源码深度解析以及与HashMap的区别

HashMap底层原理及jdk1.8源码解读吐血整理1.3w字长文

c++之引用（五千字长文详解！）

四千字从源码分析ConcurrentHashMap的底层原理（JDK1.8）