用Python模拟高尔顿钉板实验

Posted 2021-12-05 天元浪子

昨天刚刚在油管上看过弗朗西斯·高尔顿的故事，今天就在CSDN上见到有人提问如何用Python模拟高尔顿钉板实验。

提到高尔顿，人们总是把他和钉板实验联系在一起，偶尔也会有人提及他是达尔文的表弟。实际上，作为维多利亚时代的人类学家、统计学家、心理学家和遗传学家，同时又是热带探险家、地理学家、发明家、气象学家，高尔顿简直就是一位集大成者。

高尔顿钉板形如上图所示：木板上钉有锥形排列的多层钉子，每颗钉子的水平位置正好位于下一层的两颗钉子正中间；小球在下落的过程中碰到钉子之后，可能从左边滚落，也可能从右边滚落，概率都是1/2；穿过m-1层钉板后，小圆球最终会落入下方的m个容器的某一个中。

这个实验之所以有名，是因为实验结果服从正态分布。不过也有人说，高尔顿钉板的实验结果服从二项分布，只是二项分布的概率密度函数可以用正态分布近似而已，和正态分布没什么关系。我不懂数学，只好把两种说法都罗列在这里，供读者参考。

好了，明白了高尔顿钉板的原理，就该程序员一展身手了。先定义一个函数，实现小球穿过m-1层钉板后落到m个容器的某一个中，容器编号从0开始。

>>> import random
>>> def galton(m):
	pos = 0
	for i in range(1, m):
		if random.random() > 0.5:
			pos += 1
	return pos

>>> galton(9)
4
>>> galton(9)
5
>>> galton(9)
4
>>> galton(9)
4
>>> galton(9)
2

这样测试太慢了，我们干脆把测试次数n也传到函数中。

>>> def galton(m, n):
	result = [0 for i in range(m)]
	for i in range(n):
		pos = 0
		for j in range(1, m):
			if random.random() > 0.5:
				pos += 1
		result[pos] += 1
	return result

>>> galton(9, 100)
[0, 7, 13, 19, 30, 19, 10, 2, 0]

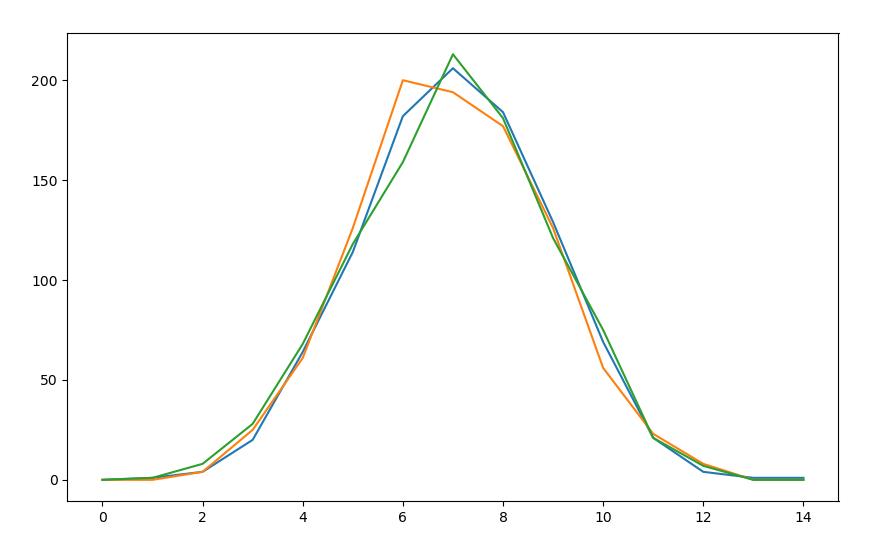
看起来的确很像正态分布的样子。我们不妨用matplotlib画出多条曲线看看，这次是14层钉板1000个小球，测试3次。

>>> import matplotlib.pyplot as plt
>>> for i in range(3):
	plt.plot(galton(15, 1000))

	
[<matplotlib.lines.Line2D object at 0x0000020938174D88>]
[<matplotlib.lines.Line2D object at 0x000002093817FF08>]
[<matplotlib.lines.Line2D object at 0x0000020938185708>]
>>> plt.show()

结果如下图所示。实验完成。