车间调度基于matlab模拟退火算法求解车间调度(jobshop-3)问题含Matlab源码 1082期

Posted 2021-12-04 紫极神光

一、车间调度简介

1 车间调度定义
车间调度是指根据产品制造的合理需求分配加工车间顺序，从而达到合理利用产品制造资源、提高企业经济效益的目的。车间调度问题从数学上可以描述为有n个待加工的零件要在m台机器上加工。问题需要满足的条件包括每个零件的各道工序使用每台机器不多于1次，每个零件都按照一定的顺序进行加工。

2 传统作业车间调度
传统作业车间带调度实例

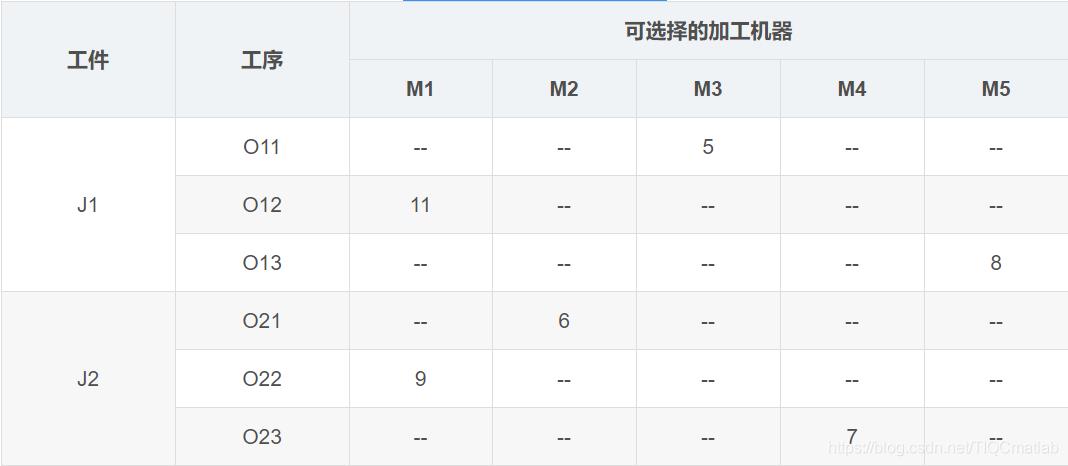
有若干工件，每个工件有若干工序，有多个加工机器，但是每道工序只能在一台机器上加工。对应到上面表格中的实例就是，两个工件，工件J1有三道工序，工序Q11只能在M3上加工，加工时间是5小时。
约束是对于一个工件来说，工序的相对顺序不能变。O11->O12->O13。每时刻，每个工件只能在一台机器上加工；每个机器上只能有一个工件。
调度的任务则是安排出工序的加工顺序，加工顺序确定了，因为每道工序只有一台机器可用，加工的机器也就确定了。
调度的目的是总的完工时间最短（也可以是其他目标）。举个例子，比如确定了O21->O22->O11->O23->O12->O13的加工顺序之后，我们就可以根据加工机器的约束，计算出总的加工时间。
M2加工O21消耗6小时，工件J2当前加工时间6小时。
M1加工O22消耗9小时，工件J2当前加工时间6+9=15小时。
M3加工O11消耗5小时，工件J1当前加工时间5小时。
M4加工O23消耗7小时，工件J2加工时间15+7=22小时。
M1加工O12消耗11小时，但是要等M1加工完O22之后才开始加工O12，所以工件J1的当前加工时间为max(5,9)+11=20小时。
M5加工O13消耗8小时，工件J2加工时间20+8=28小时。
总的完工时间就是max(22,28)=28小时。

2 柔性作业车间调度
柔性作业车间带调度实例（参考自高亮老师论文
《改进遗传算法求解柔性作业车间调度问题》——机械工程学报）

相比于传统作业车间调度，柔性作业车间调度放宽了对加工机器的约束，更符合现实生产情况，每个工序可选加工机器变成了多个，可以由多个加工机器中的一个加工。比如上表中的实例，J1的O12工序可以选择M2和M4加工，加工时间分别是8小时和4小时，但是并不一定选择M4加工，最后得出来的总的完工时间就更短，所以，需要调度算法求解优化。

相比于传统作业车间，柔性车间作业调度的调度任务不仅要确定工序的加工顺序，而且需要确定每道工序的机器分配。比如，确定了O21->O22->O11->O23->O12->O13的加工顺序，我们并不能相应工序的加工机器，所以还应该确定对应的[M1、M3、M5]->[M1、M2、M3]->[M1、M2、M3、M4、M5]->[M2、M3、M4、M5]->[M2、M4]->[M1、M3、M4、M5]的机器组合。调度的目的还是总的完工时间最短（也可以是其他目标，比如机器最大负荷最短、总的机器负荷最短）

二、模拟退火算法简介

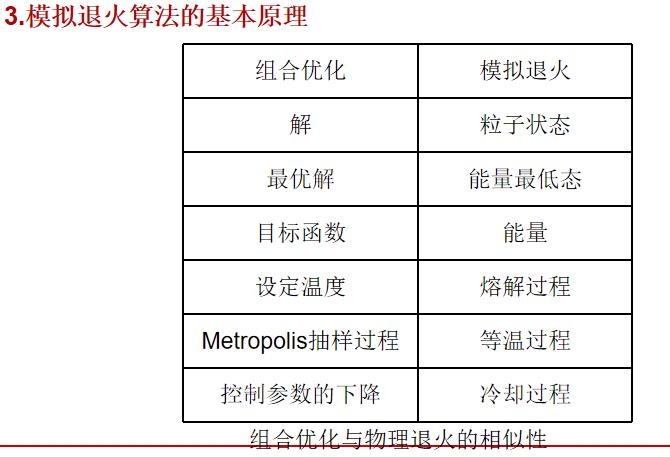
5 模拟退火算法的参数
模拟退火是一种优化算法，它本身是不能独立存在的，需要有一个应用场合，其中温度就是模拟退火需要优化的参数，如果它应用到了聚类分析中，那么就是说聚类分析中有某个或者某几个参数需要优化，而这个参数，或者参数集就是温度所代表的。它可以是某项指标，某项关联度，某个距离等等。

三、部分源代码

clc
clear
%=========数据录入，参数调整=================
swarminitNum=20;%初始生成的粒子数；

MM=[1 2 3 4 5 6 
    6 6 6 6 6 6];%工件、工序数量矩阵，MM第一行表示工件，第二行表示每个工件的工序数；

machineNum=6;   %加工机器数；

initT=500;          %模拟退火初始温度；

gen=1000;        %循环迭代数；

w1=0.35;          %变异率；

changeNum=3;     %变异变换对数；

restrictmatrixM=[3     1     2     4     6     5
                 2     3     5     6     1     4
                 3     4     6     1     2     5
                 2     1     3     4     5     6
                 3     2     5     6     1     4
                 2     4     6     1     5     3];%job-shop机器约束矩阵；
             
restrictmatrixT=[1     3     6    7      3     6
                 8     5     10   10     10    4
                 5     4     8     9     1     7
                 5     5     5     3     8     9
                 9     3     5     4     3     1
                 3     3     9     10    4     1];%job-shop时间约束矩阵；
             
%===============PSO算法==========================
swarminit=cell(1,swarminitNum);
swarminitLong=sum(MM(2,:));          %所有工序数即粒子长度；
for i=1:swarminitNum,
    swarminit{i}=randomparticle(MM) ;
end                                  %随机生成初始粒子群体
[popu,s] = size(swarminit); 
trace = ones(1,gen); 
trace(1) = 10000; % 初始全局最佳适应度设为足够大 
for i = 1:s,
    bestfit(i) = 10000; % 初始个体历史最佳适应度设为足够大 
end
bestpar = swarminit; % 个体历史最佳粒子初始化
for u=1:swarminitNum,
    fitlist=[0]; 
end
T=initT;
for step = 1:gen,
    for q=1:swarminitNum,
            fitlist(q)=timedecode(swarminit{q},restrictmatrixM,restrictmatrixT,machineNum)  ;     
    end              % 计算当前粒子群每个粒子的适应度
    [minval,sub] = min(fitlist); % 求得这代粒子的适应度最小值及其下标 
    if(trace(step) > minval)  ,
         trace(step) = minval; 
         bestparticle = swarminit{sub}; 
    end
    if(step~= gen) ,
        trace(step + 1) = trace(step); % 全局最佳适应度及最佳粒子调整 
    end
    T=0.97*T;
    for i = 1:s,
        tt=fitlist(i)-bestfit(i);
        if(tt<0)|(min(1,exp(-tt/T))>=rand(1,1));
           bestfit(i) = fitlist(i); 
           bestpar{i} = swarminit{i}; 
       end 
   end % 个体历史最佳粒子及适应度调整 ；
   for j = 1:s,
       if rand(1,1)<w1,
          bestparticle1=bianyi(bestparticle,changeNum,swarminitLong);
       else
           bestparticle1=bestparticle;
       end               %粒子变异；
       l1=1000;
       l2=1;
       l3=1000;
       l4=1;
       while (l1-l2)>swarminitLong,
           m=fix(swarminitLong*rand(1,1));
           n=fix(swarminitLong*rand(1,1));
           l1=max(m,n)+1;
           l2=min(m,n)+1;
       end
       while (l3-l4)>swarminitLong,
           m1=fix(swarminitLong*rand(1,1));
           n1=fix(swarminitLong*rand(1,1));
           l3=max(m1,n1)+1;
           l4=min(m1,n1)+1;
       end
       swarminit{j}=cross(bestpar{j},swarminit{j},l2,l1);
       swarminit{j}=cross(bestparticle1,swarminit{j},l4,l3);%粒子交叉；
   end 
end
function gant(particle,swarminitLong,restrictmatrixM,restrictmatrixT,b)
%particle=[1.0	1.0	3.0	2.0	3.0	4.0	2.0	6.0	4.0	3.0	1.0	6.0	5.0	5.0	6.0	4.0	3.0	2.0	4.0	3.0	2.0	5.0	4.0	6.0	1.0	2.0	1.0	5.0	5.0	6.0	1.0	4.0	2.0	6.0	3.0	5.0];
% restrictmatrixM=[      3     1     2     4     6     5
%                        2     3     5     6     1     4
%                        3     4     6     1     2     5
%                        2     1     3     4     5     6
%                        3     2     5     6     1     4
%                        2     4     6     1     5     3];

%restrictmatrixT=    [    1     3     6    7      3     6
%                         8     5     10   10     10    4
%                         5     4     8     9     1     7
%                         5     5     5     3     8     9
%                         9     3     5     4     3     1
%                         3     3     9     10    4     1];
%                     swarminitLong=36;
for i=1:6
    counter(i)=[1] ; %位置计数器
    s(i)=[0]  ;      %工件上一工序结束时间
    t(i)=[0]  ;      %机器上一工序结束时间   
end  
for j=1:swarminitLong,
    k=particle(j);
    time(k,counter(k))=restrictmatrixT(k ,counter(k)) ;      
    %时间矩阵解码
    machine(k,counter(k))=restrictmatrixM(k,counter(k));
    %机器矩阵解码
    
    
    [rom]=max( s(k), t(machine(k,counter(k))) );
    s(k)=rom+time(k,counter(k));
    t(machine(k,counter(k)))=rom+time(k,counter(k));
    %计算每台机器上加工时间   
    %生成甘特图
    x=[rom t(machine(k,counter(k)))];
    y=[machine(k,counter(k)) machine(k,counter(k))];
    x1=[t(machine(k,counter(k)))-0.1 t(machine(k,counter(k)))];
    y1=[machine(k,counter(k)) machine(k,counter(k))];
    plot(x,y,'LineWidth',7.5,'Color','k');
    hold on
    plot(x1,y1,'LineWidth',7.5,'Color','white');
    hold on
    a=k*10+counter(k);

    text((rom+t(machine(k,counter(k))))/2-1,machine(k,counter(k))-0.5,num2str(a))  ;
    %    text((rom+t(machine(k,counter(k))))/2-1,machine(k,counter(k))-0.5,num2str(a))  ;
    hold on
    axis([0 b+5 0 7]) ;


    counter(k)=counter(k)+1   ;
end
 xlabel('time(minute)');
 ylabel('machine');
 title('甘特图');

四、运行结果

五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.