动态规划背包题目总结

Posted 2021-12-04 karshey

01背包问题

模板题

acw 2. 01背包问题

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1005;
int v[N],w[N],dp[N];
int main()
{
	int n,vv;cin>>n>>vv;
	for(int i=0;i<n;i++)
	{
		cin>>w[i]>>v[i];
	}
	for(int i=0;i<n;i++)
	{
		for(int j=vv;j>=w[i];j--)
		{
			dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
		}
	}
	cout<<dp[vv];
	return 0; 
}

xinjun与阴阳师

xinjun与阴阳师
注意是先输入ai个w，再输入ai个v，而不是两种一起输入。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1005;
//一种模式只有一种操作，但是可以有多种模式，所以不能直接打散
struct node
{
	int size;
	int v[N],w[N];
}a[N];
int dp[N];
int main()
{
	ios::sync_with_stdio(false);
	int t,n,m;cin>>t;
	while(t--)
	{
		memset(dp,0,sizeof(dp));
		cin>>n>>m;		
		for(int i=0;i<n;i++) 
		{
			cin>>a[i].size;
			for(int j=0;j<a[i].size;j++)
			{
				//先价值后容量
				cin>>a[i].w[j];				
			}
			for(int j=0;j<a[i].size;j++)
			{			
				cin>>a[i].v[j];				
			}
		}		
		
		//01背包
		for(int i=0;i<n;i++)
		{
			for(int j=m;j>=0;j--)
			{
				for(int k=0;k<a[i].size;k++)
				{
					if(j>=a[i].v[k]) dp[j]=max(dp[j],dp[j-a[i].v[k]]+a[i].w[k]);
				}
			}
		}
		cout<<dp[m]<<endl; 
	}
	return 0; 
}

Rabbit的工作(2)

Rabbit的工作(2)
一共n天，共有k个任务，用i天完成任务会获得w[i]的满意度，老板要求在V天内完成。
首先任务是都要完成的，所以可以先花k天把任务都完成，然后用剩余的V-k天dp得到可能的最大满意度。
注意：要初始化为负无穷，因为在先花一天完成所有后w[i]可能为负数！（即两天的满意度小于一天的满意度的情况）
而且，在花完一天完成所有之后，再花一天的价值其实是w[2]！

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=4005;
int w[N],dp[N];
int main()
{
	int n,k,V;cin>>n>>k>>V;
	for(int i=1;i<=n;i++) cin>>w[i];
	for(int i=2;i<=n;i++) w[i]-=w[1];
	int ans=k*w[1];
	V-=k;
	fill(dp,dp+4005,-1e9);
	dp[0]=0;
	for(int i=1;i<n;i++)
	{
		for(int j=i;j<=V;j++)
		{
			dp[j]=max(dp[j],dp[j-i]+w[i+1]);
		}
	}
	cout<<dp[V]+ans;
	return 0; 
}

完全背包问题

笔记。

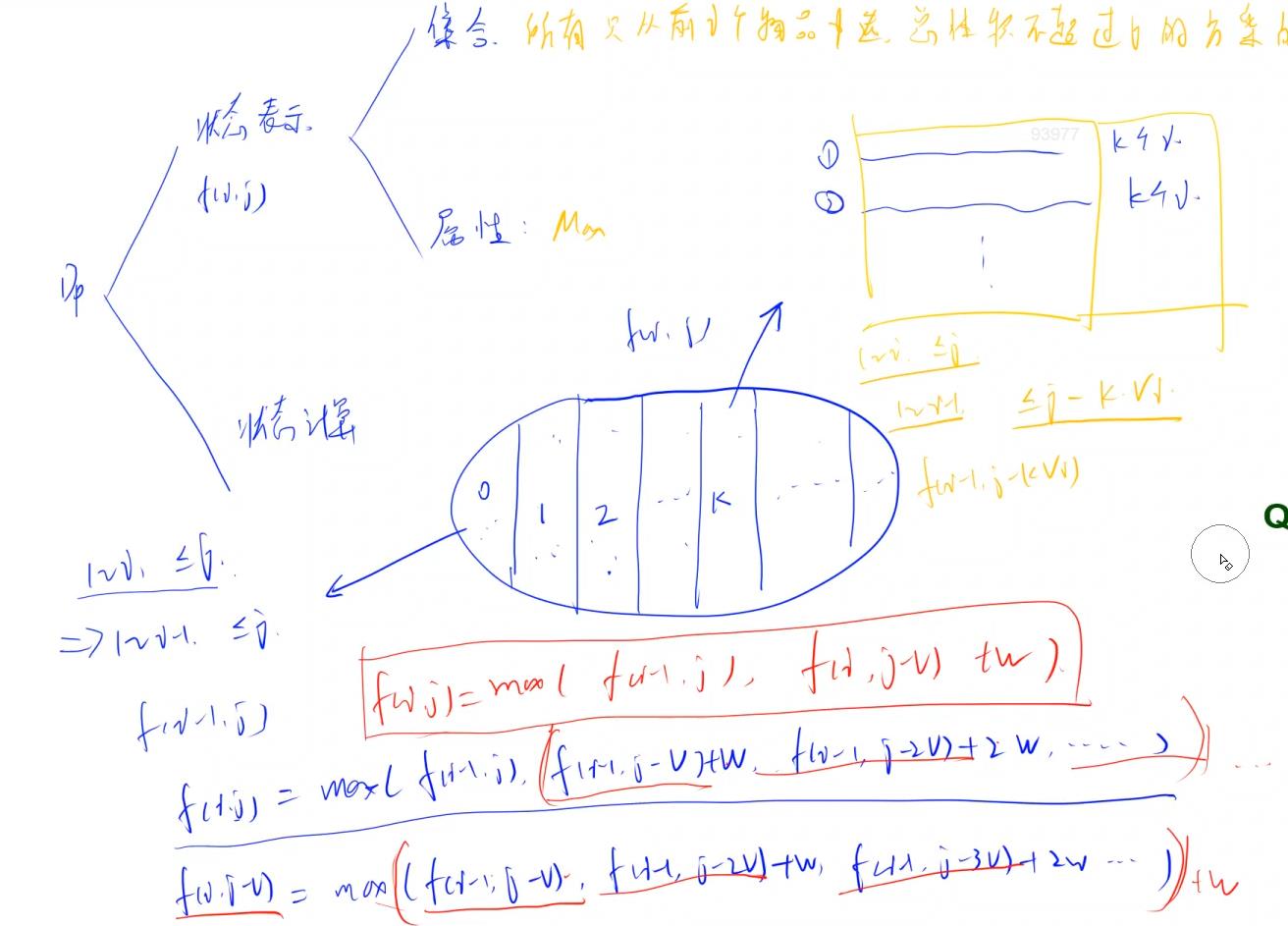
模板题

3. 完全背包问题
二维：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1005;
int v[N],w[N],dp[N][N];
int main()
{
	int n,V;cin>>n>>V;
	for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=V;j++)
		{
			dp[i][j]=dp[i-1][j];
			if(j>=v[i]) dp[i][j]=max(dp[i-1][j],dp[i][j-v[i]]+w[i]);			
		}
	}
	cout<<dp[n][V];
	return 0; 
}

一维（优化后）：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1005;
int v[N],w[N],dp[N];
int main()
{
	int n,V;cin>>n>>V;
	for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
	for(int i=1;i<=n;i++)
	{
		for(int j=v[i];j<=V;j++)
		{
			dp[j]=max(dp[j],dp[j-v[i]]+w[i]);	
		}
	}
	cout<<dp[V];
	return 0; 
}

小明打联盟

小明打联盟
先对每个招数的时间和伤害dp一次，再最后对大招的时间dp一次。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10;
ll v[6],w[6],dp[N];
int main()
{
	ll t,l,r,temp,A;
	while(cin>>t)
	{
		for(int i=1;i<=3;i++) cin>>v[i]>>w[i];
		cin>>l>>r>>temp>>A;
		v[4]=l;w[4]=temp;
		v[5]=r;w[5]=temp+A*(r-l);//分别是最小大招和最大大招
		
		memset(dp,0,sizeof(dp));
		for(int i=1;i<=5;i++)
		{
			for(ll j=v[i];j<=t;j++)
			{
				dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
			}
		}
		
		//对大招时间的dp
		for(int i=l;i<=r;i++) 
		{
			dp[t]=max(dp[t],dp[t-i]+temp+(i-l)*A);
		}
		cout<<dp[t]<<endl;
	}
	return 0; 
}

参考了小明打联盟 背包问题