王道数据结构与算法特殊矩阵的压缩存储
Posted 生命是有光的
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了王道数据结构与算法特殊矩阵的压缩存储相关的知识,希望对你有一定的参考价值。
✍、目录脑图
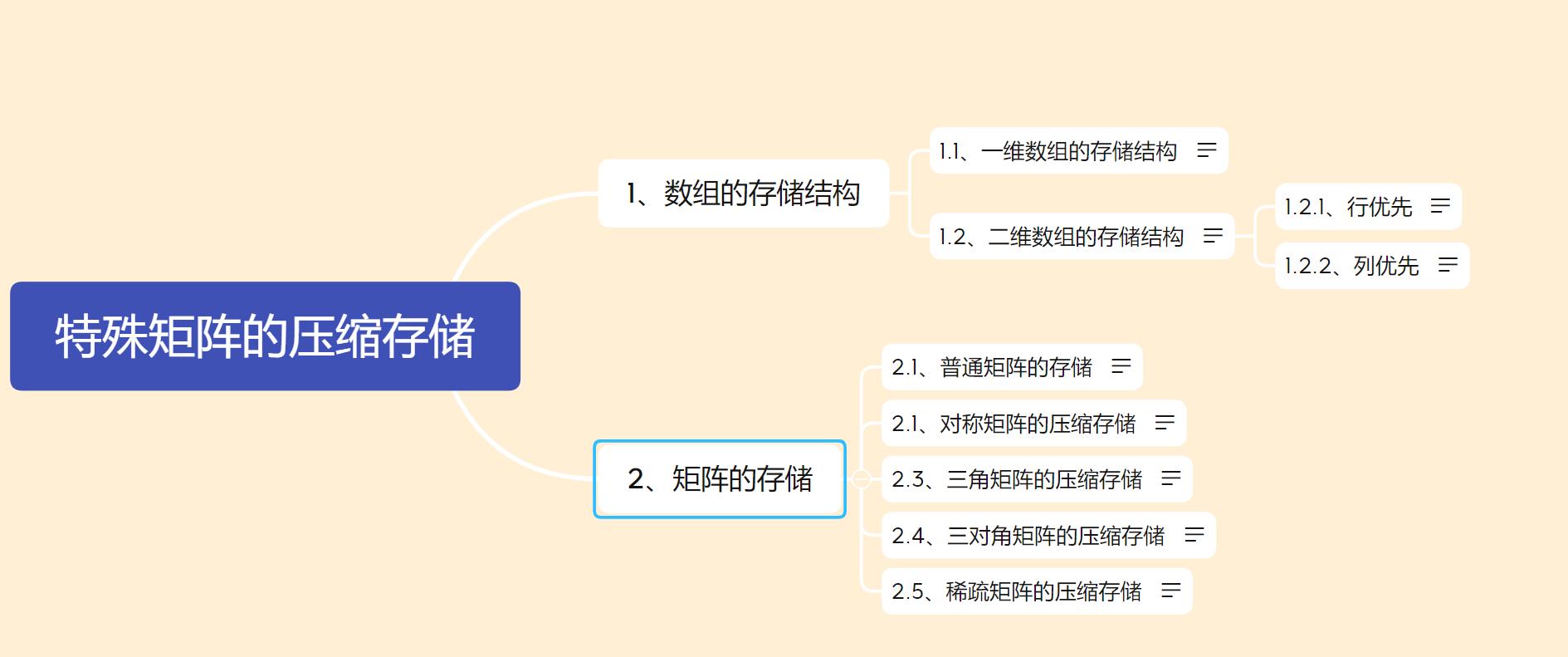
1、数组的存储结构
1.1、一维数组的存储结构

1.2、二维数组的存储结构

-
行优先:先存行,一行存完存第二行
-
列优先:先存列,一列存完存第二列
我们采用行优先或者列优先的存储方式存放二维数组,这样我们就可以通过二维数组的行号和列号来计算出这个元素所对应的存储地址。
1.2.1、行优先
我们来看行优先的一个例子

M 行 N 列的二维数组 b [M] [N] 中,若按行优先存储,则 b [i] [j] 的存储地址 = 起始地址LOC + (i*N+j) * sizeof(ElemType)
- (i * N + j) 指的是 b[i] [j] 之前有多少个元素,每个元素再乘存储空间,就是 b[i] [j] 元素前面的存储空间
- 再加上起始地址 LOC,就得到 b[i] [j] 的存储地址
1.2.2、列优先

M 行 N 列的二维数组 b [M] [N] 中,若按列优先存储,则 b [i] [j] 的存储地址 = 起始地址LOC + (j*M+i) * sizeof(ElemType)
- (j*M+i)指的是 b[i] [j] 之前有多少个元素, 每个元素再乘存储空间,就是 b[i] [j] 元素前面的存储空间
- 再加上起始地址 LOC,就得到 b[i] [j] 的存储地址
2、矩阵的存储
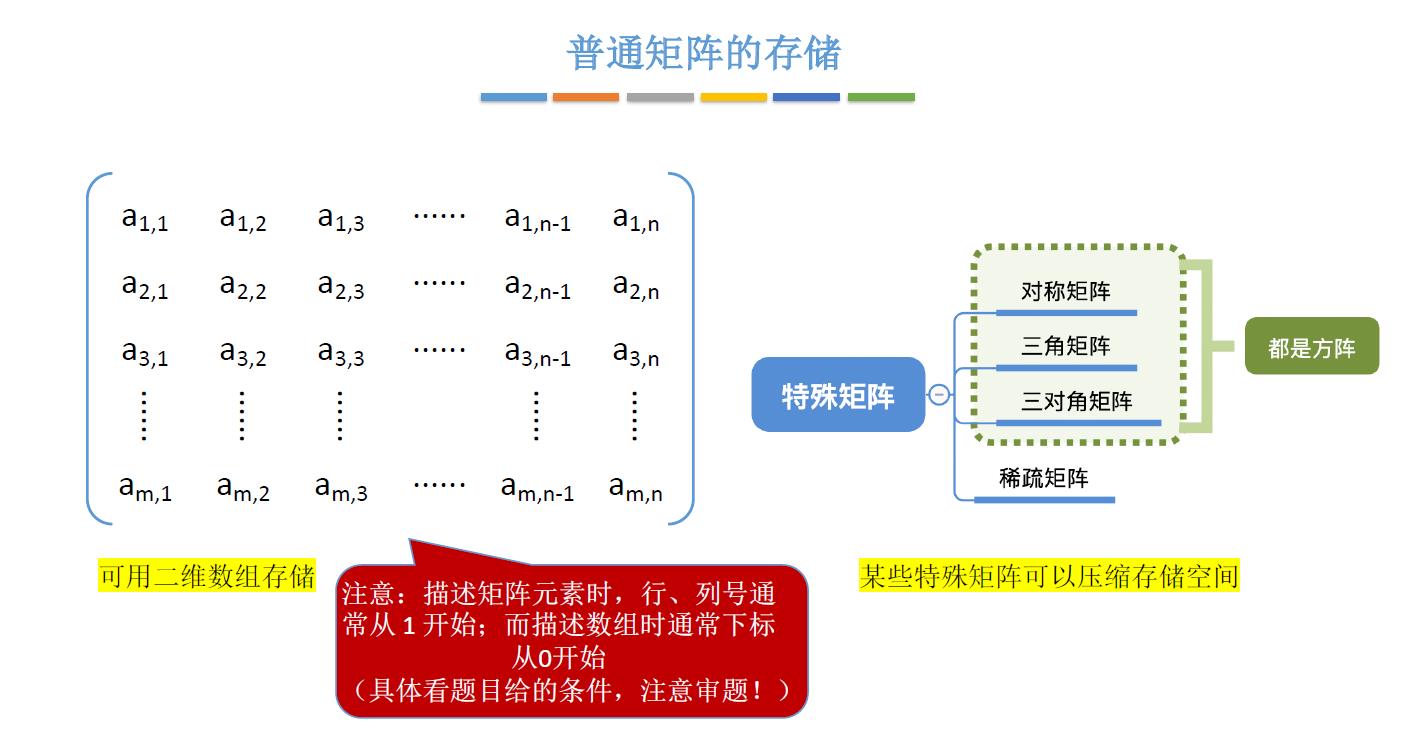
2.1、普通矩阵的存储
2.1、对称矩阵的压缩存储
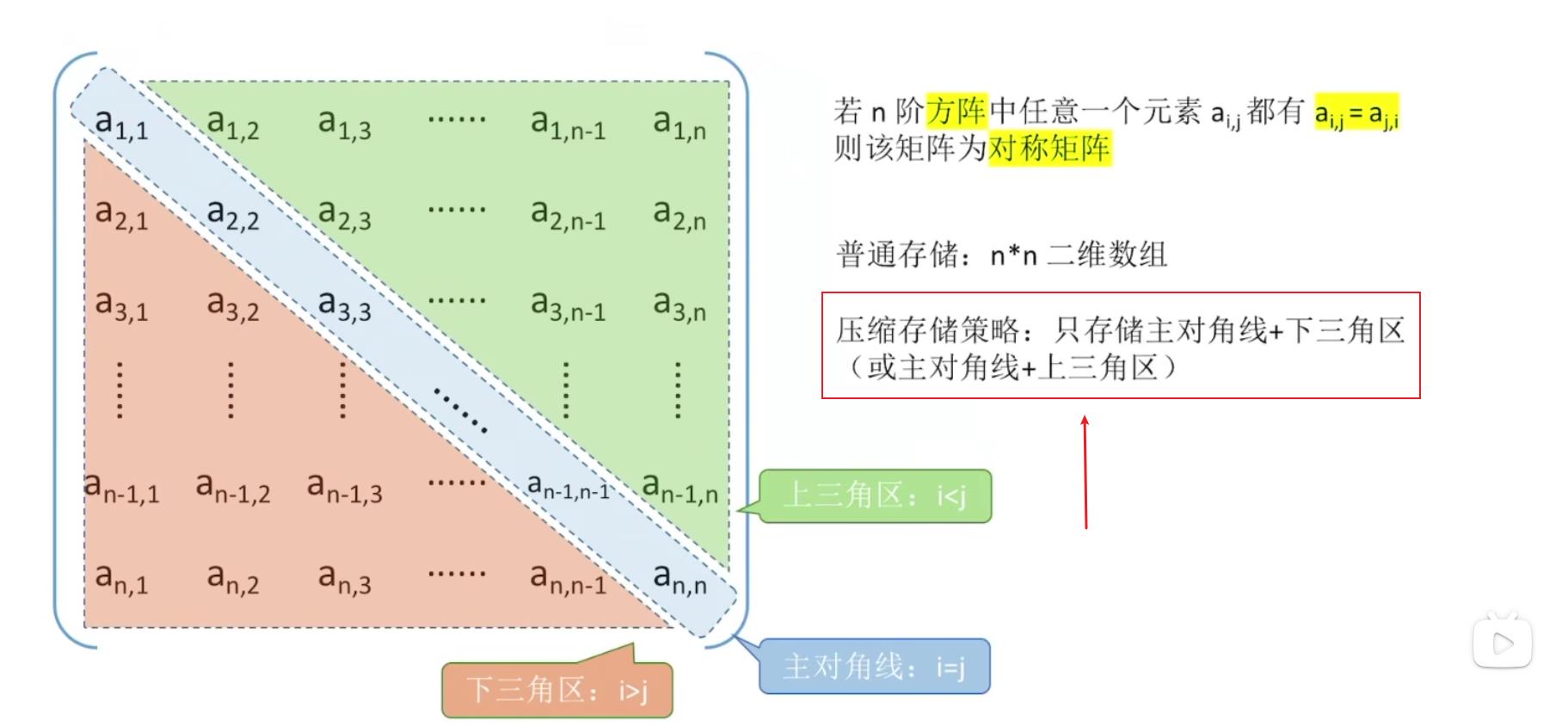
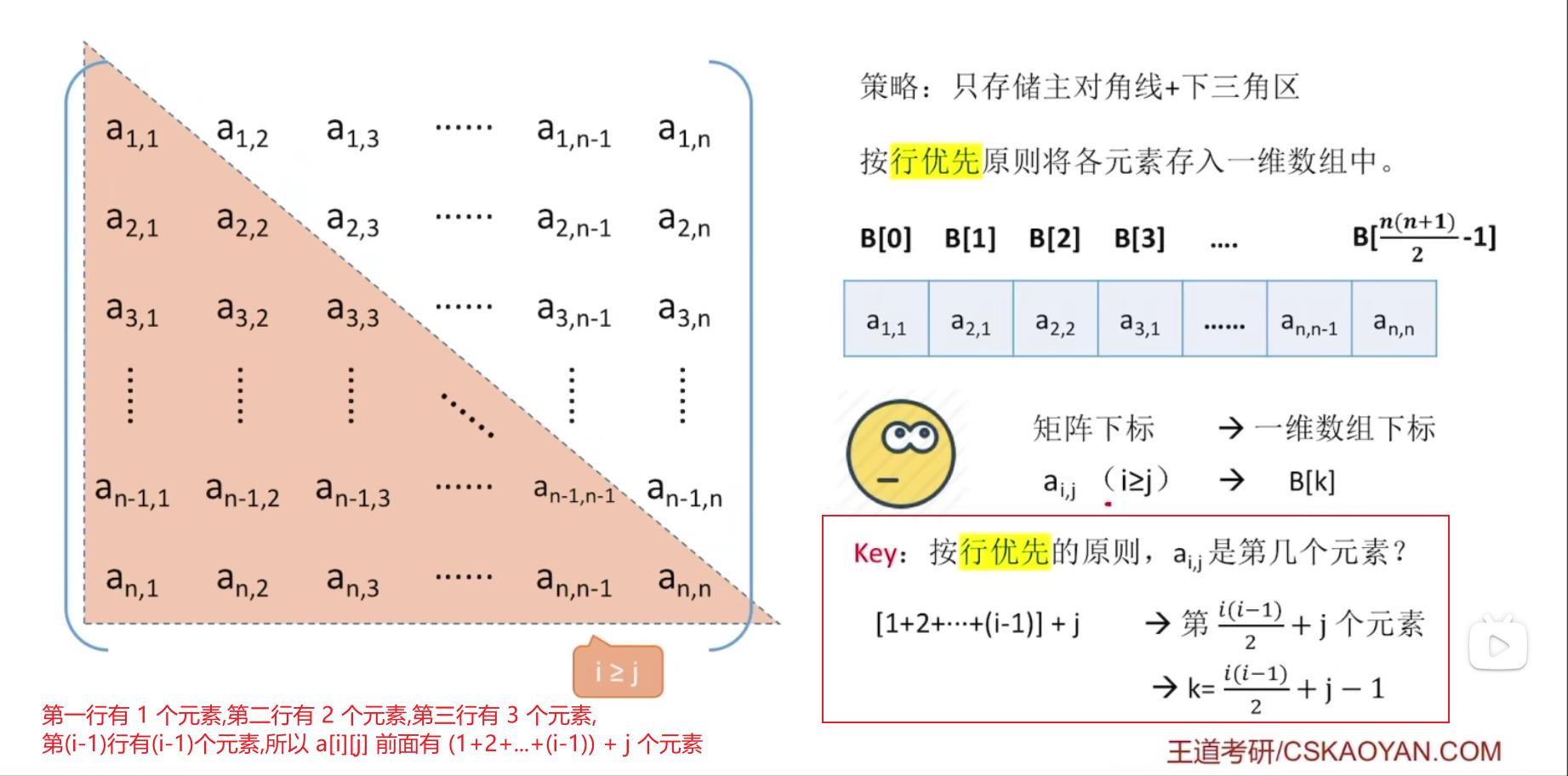
- 策略:只存储主对角线 + 下三角区
- 按行优先原则将各元素存入一维数组中,共存 (1+n)*n/2 个元素,由于一维数组下标从 0 开始,所以最后一个元素下标是 (1+n) * n/2 - 1
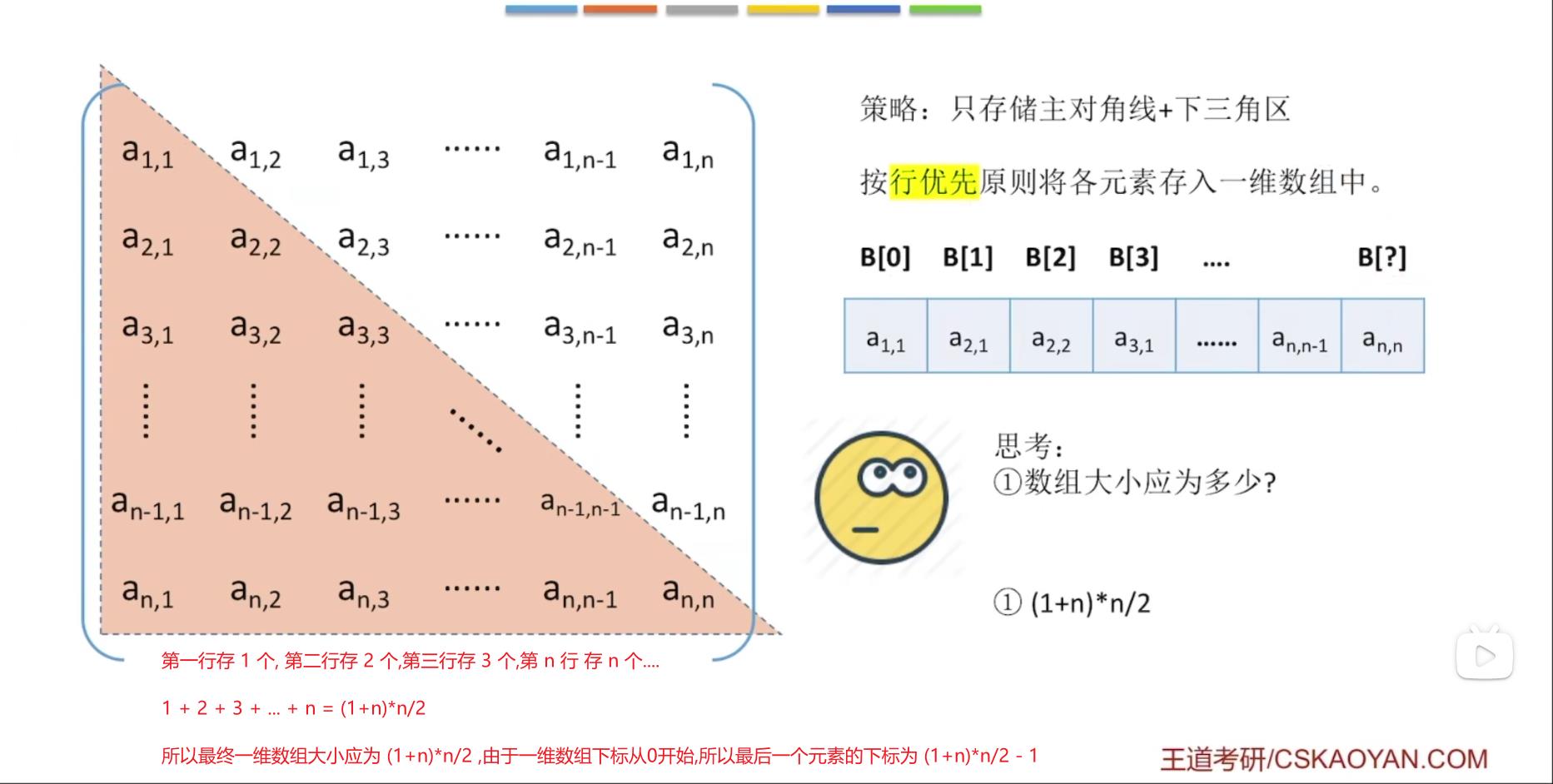
我们最终的目的是将矩阵压缩存储后怎样才能方便使用,这样我们就可以建立一个映射函数,矩阵下标 -> 一维数组下标,这样我们想要访问矩阵中某一行某一列的元素时,只需要通过映射函数一转,就可以知道它存放在一维数组的哪个位置。如何做呢?
-
按行优先的原则,a[i] [j] 是第 (1+2+…+(i-1)) + j 个元素,但是由于一维数组下标是从 0 开始的,所以对应的一维数组下标为==(1+2+…+(i-1)) + j -1==
-
但是如果我们想访问上三角区的元素呢?虽然上三角区并没有进行存储,但是由于对称矩阵的特性,a[i] [j] = a[j] [i],我们可以进行转换,相当于我们访问的仍然是下三角区的元素
-
按列优先的原则,第一列存储n个元素,第二列存储n-1个元素,第三列存储n-2个元素,第(j-1)列总共有[n+(n-1)+(n-2)+…+(n-j+2)]个元素,所以a[i] [j] 是第 [[n+(n-1)+(n-2)+…+(n-j+2)]+(i-j)+1] 个元素
2.3、三角矩阵的压缩存储
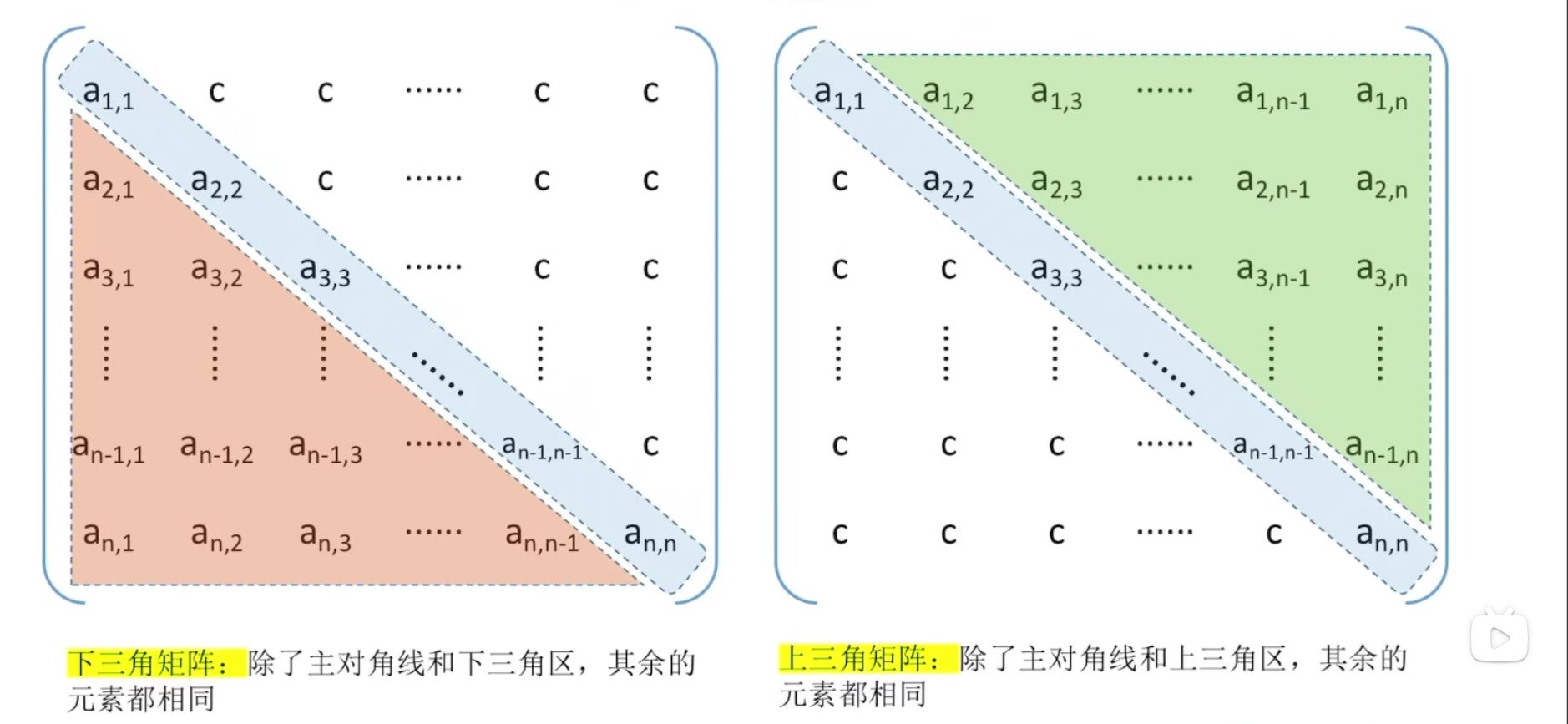
- 策略:如图
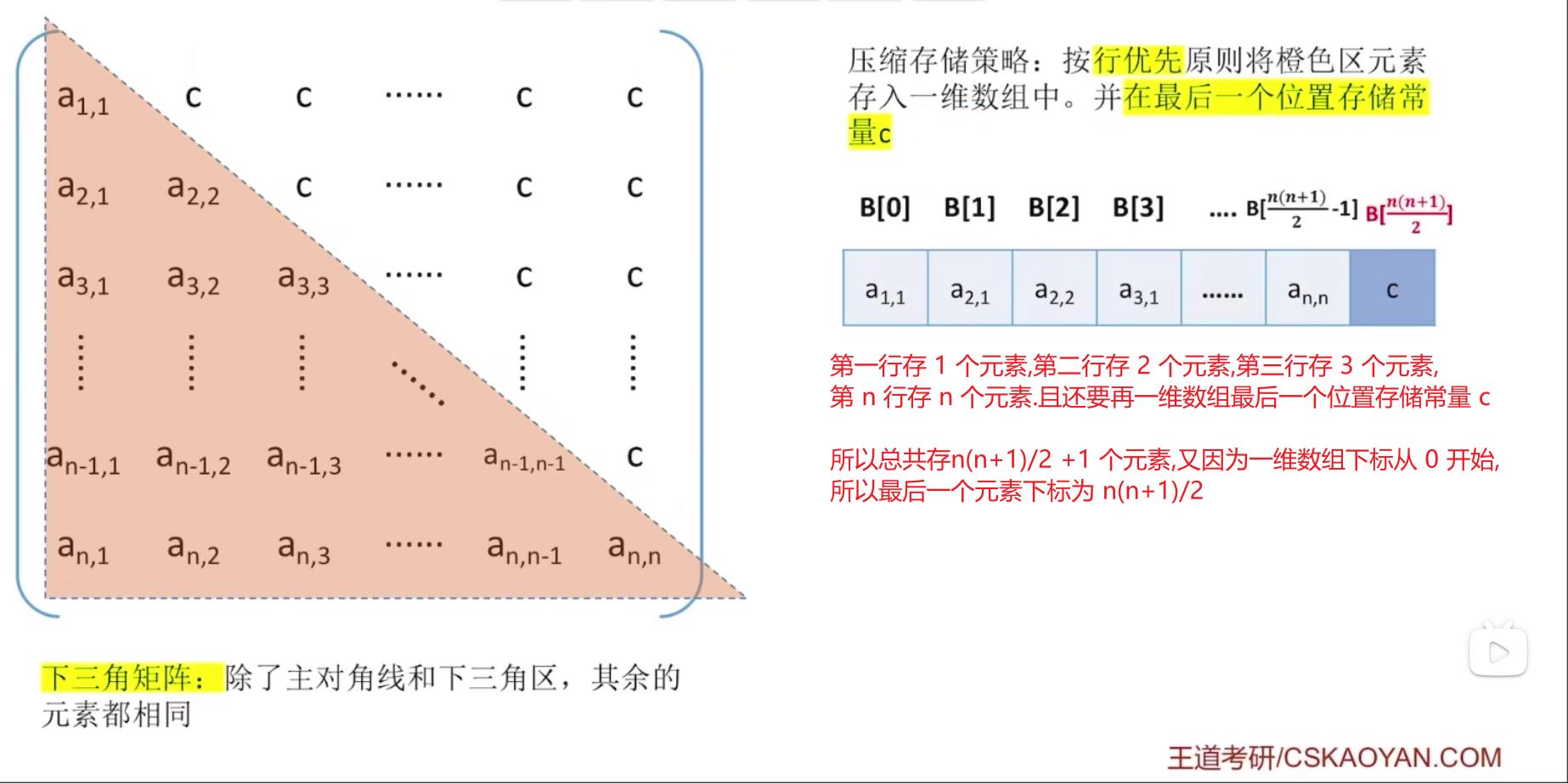
那我们如何用呢?还是建立一个映射函数,这里的映射函数与对称矩阵的映射函数一样,不同的是如果我们访问上三角区常量,我们需要将其映射为一维数组的最后一个元素,因为一维数组最后一个元素存储常量。
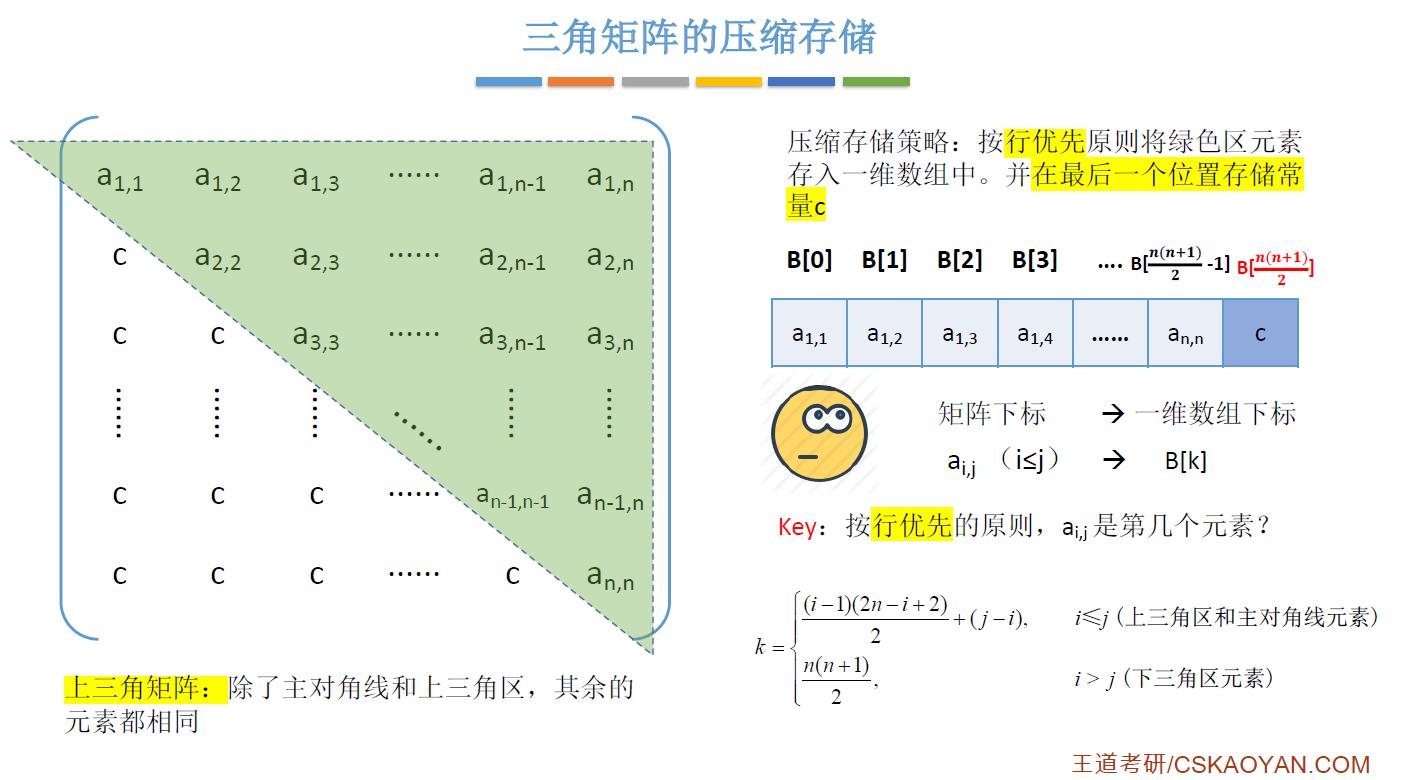
- 按行优先的原则,a[i] [j]前面有 i-1 行,第一行存储n个元素,第二行存储n-1个元素,第三行存储n-3个元素,第(i-1)行存储(n-i+2)个元素,所以a[i] [j]前面共有[[n+(n-1)+(n-2)+…+(n-i+2)+(j-i)]]个元素
2.4、三对角矩阵的压缩存储
三对角矩阵,主对角线上的元素可以不为0,主对角线上元素的上下左右相邻元素也可以不为0,但是其余元素必须为0
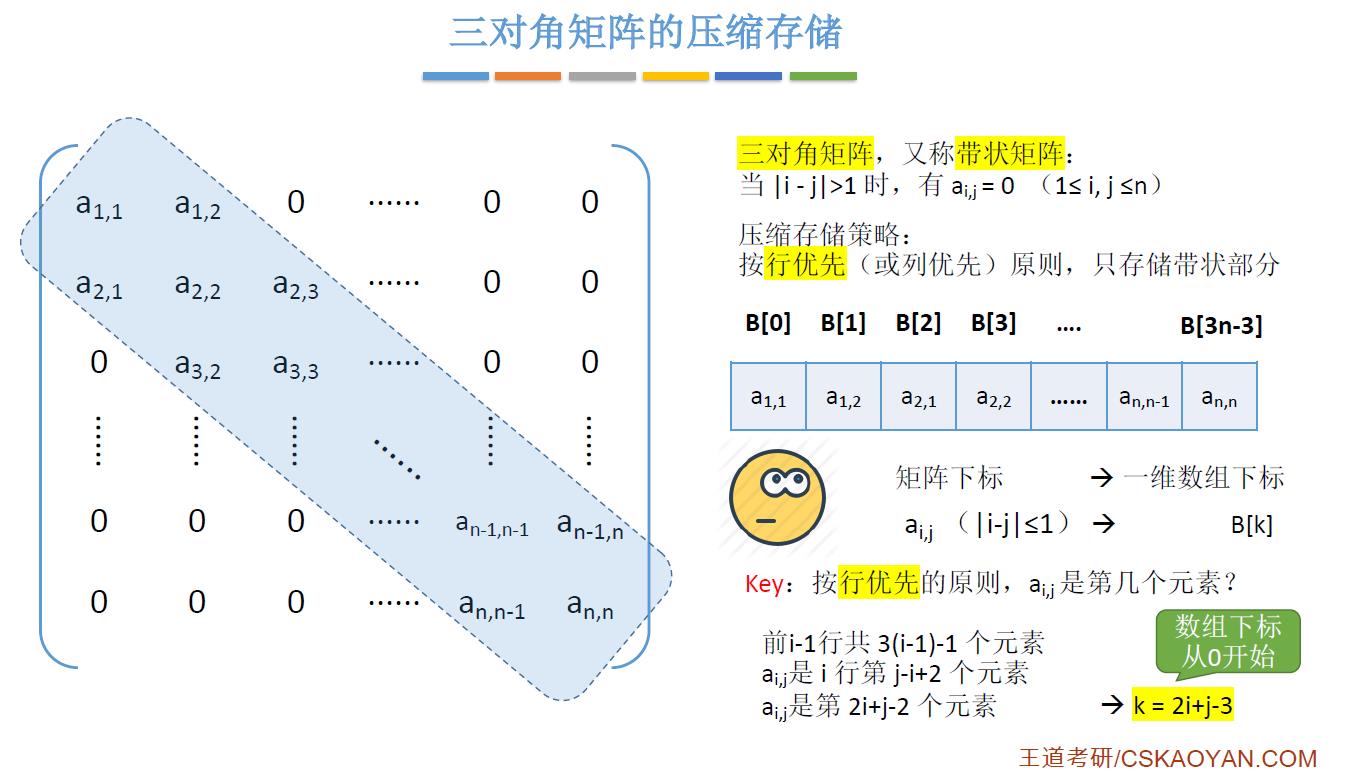
-
按行优先的原则,只存储带状部分,除了第一行和最后一行为 2 个元素,其余行均为 3 个元素,所以总共需要存储 (3n-2) 个元素,由于数组下标默认从0开始,所以最后一个数组下标为 (3n-3)
-
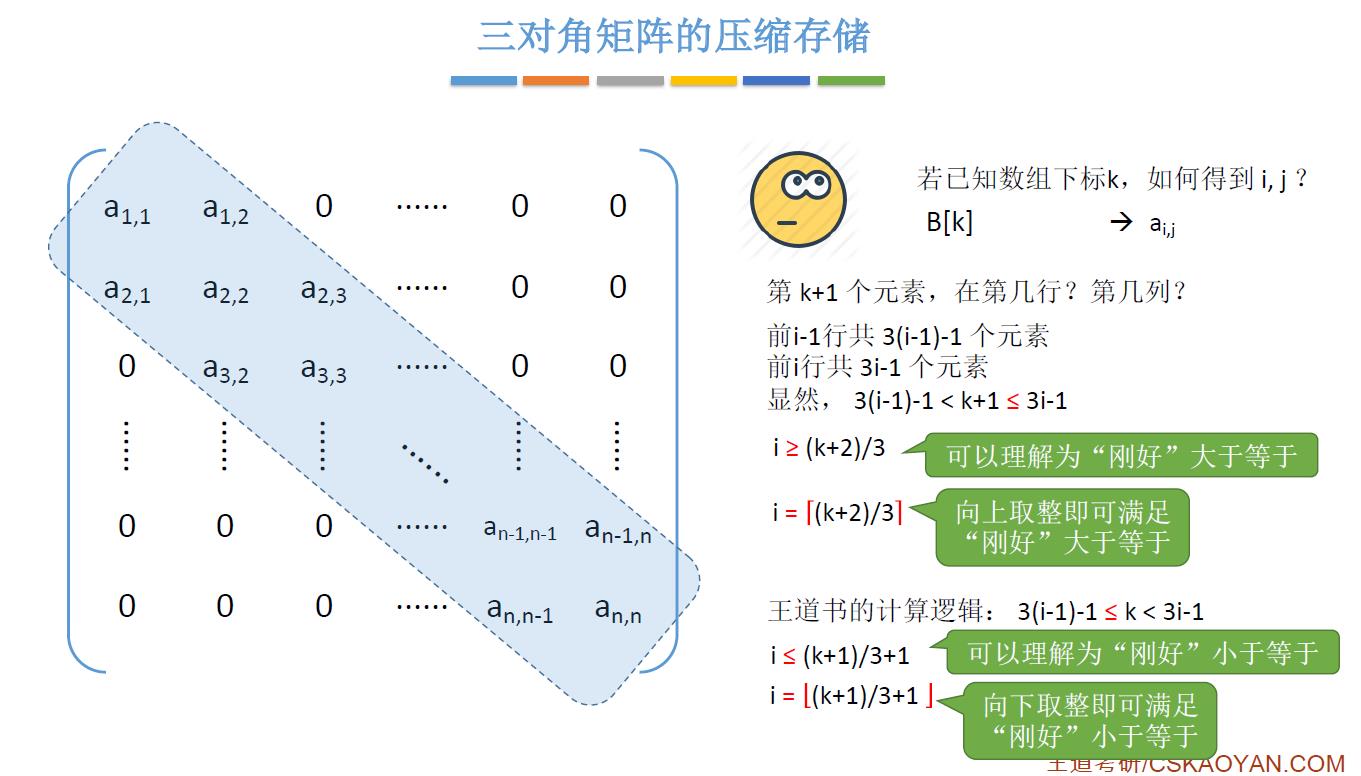
前 i-1 行共 [3(i-1)-1] 个元素
-
a[i] [j] 是 i 行的第 j-i+2 个元素
-
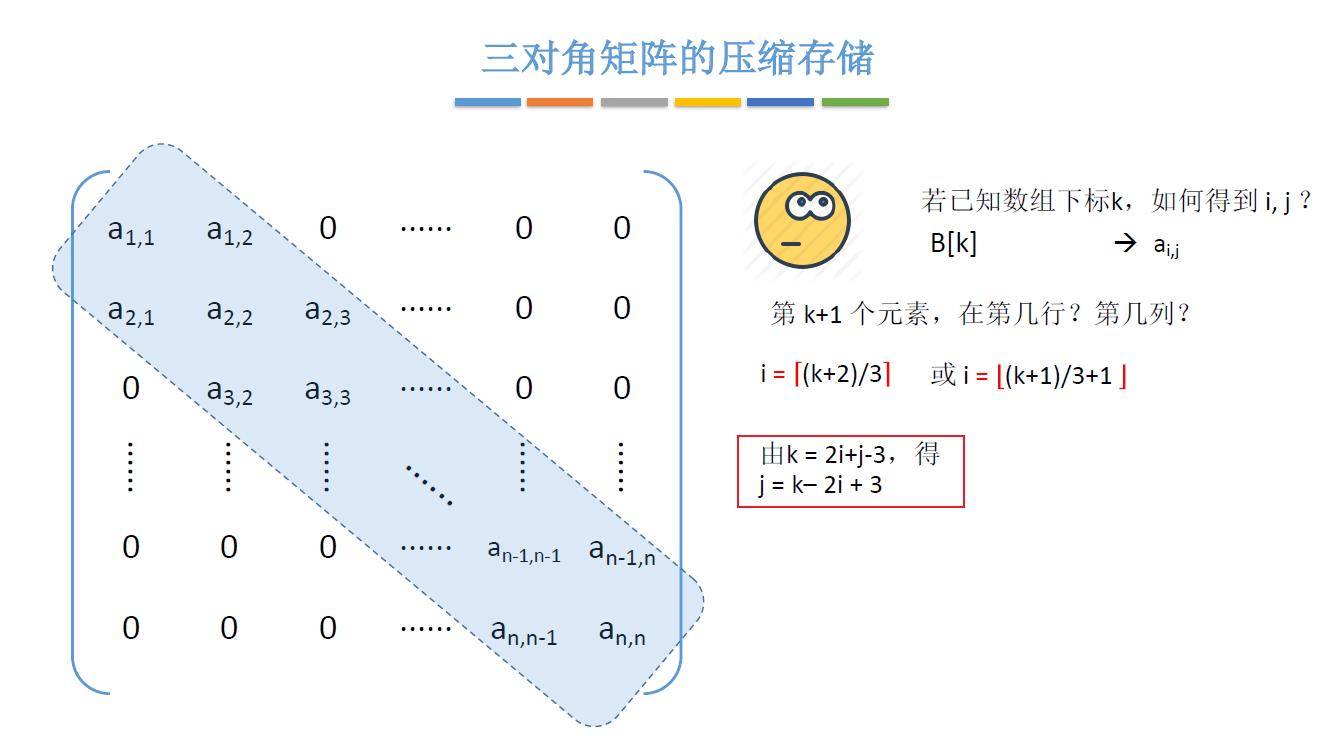
a[i] [j] 是第 2i+j-2 个元素,转化为 K = 2i+j-3
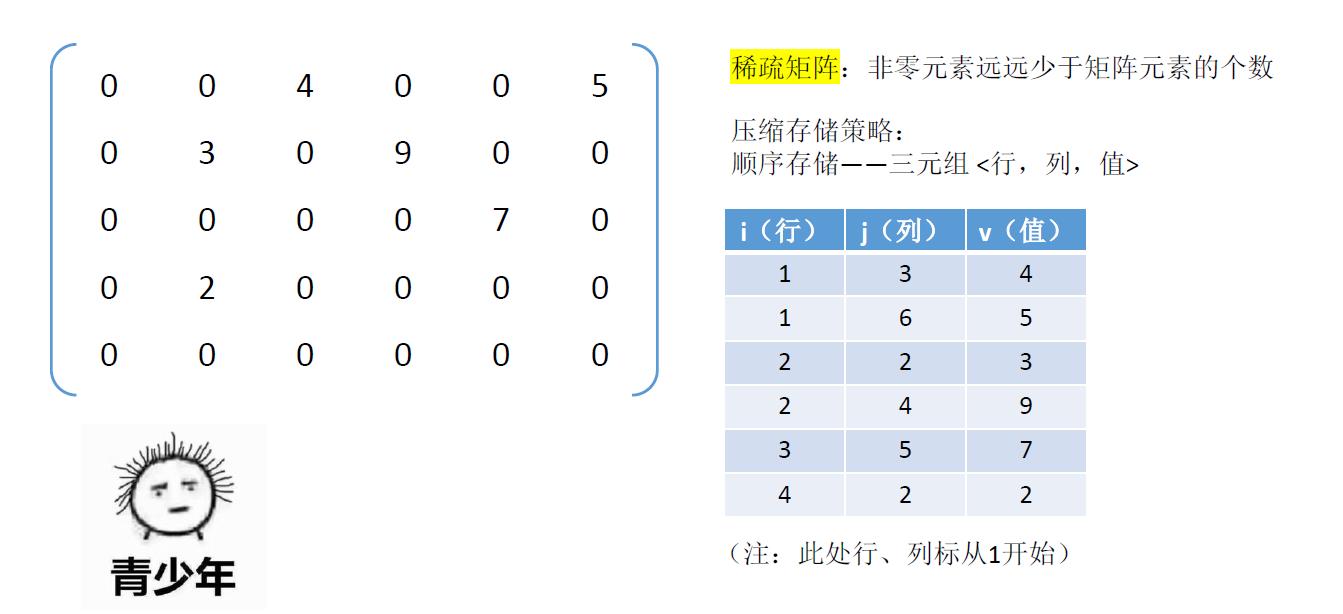
2.5、稀疏矩阵的压缩存储
可以使用三元组存储
十字链表法
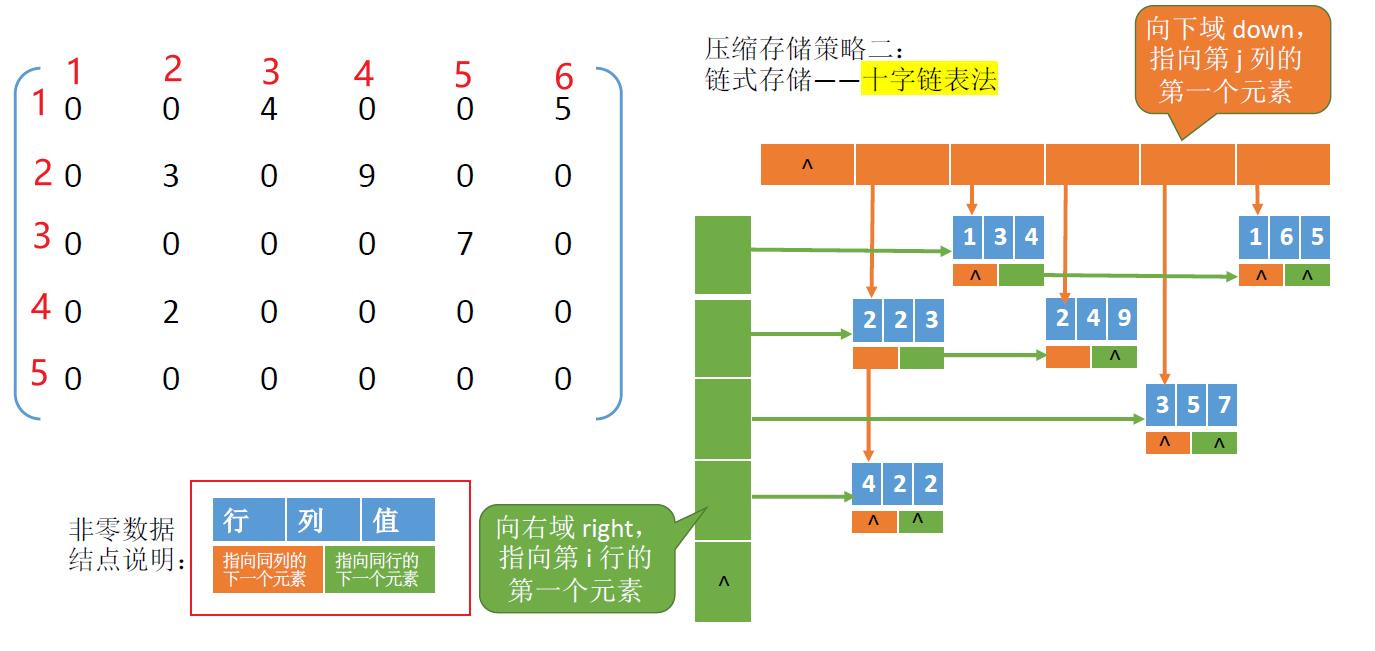
以上是关于王道数据结构与算法特殊矩阵的压缩存储的主要内容,如果未能解决你的问题,请参考以下文章