经典动态规划——从LeetCode题海中总结常见套路
Posted 沉迷单车的追风少年
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了经典动态规划——从LeetCode题海中总结常见套路相关的知识,希望对你有一定的参考价值。
前言:动态规划是算法题中最经典、最难理解、最巧妙的问题。这是一年前的旧文,当时我写了一半没有写完。现在重新整理了一下,打算分成一个系列,配合LeetCode新出的动态规划专栏,重新再把动态规划里面经典的题目整理一遍。
目录
最大路径和:LeetCode剑指offer47.礼物的最大价值
从打劫犯到按摩技师:LeetCode面试题.17.16按摩师
用贪心改善DP:LeetCode343.整数拆分&&面试题14-I.剪绳子
题目方法总览
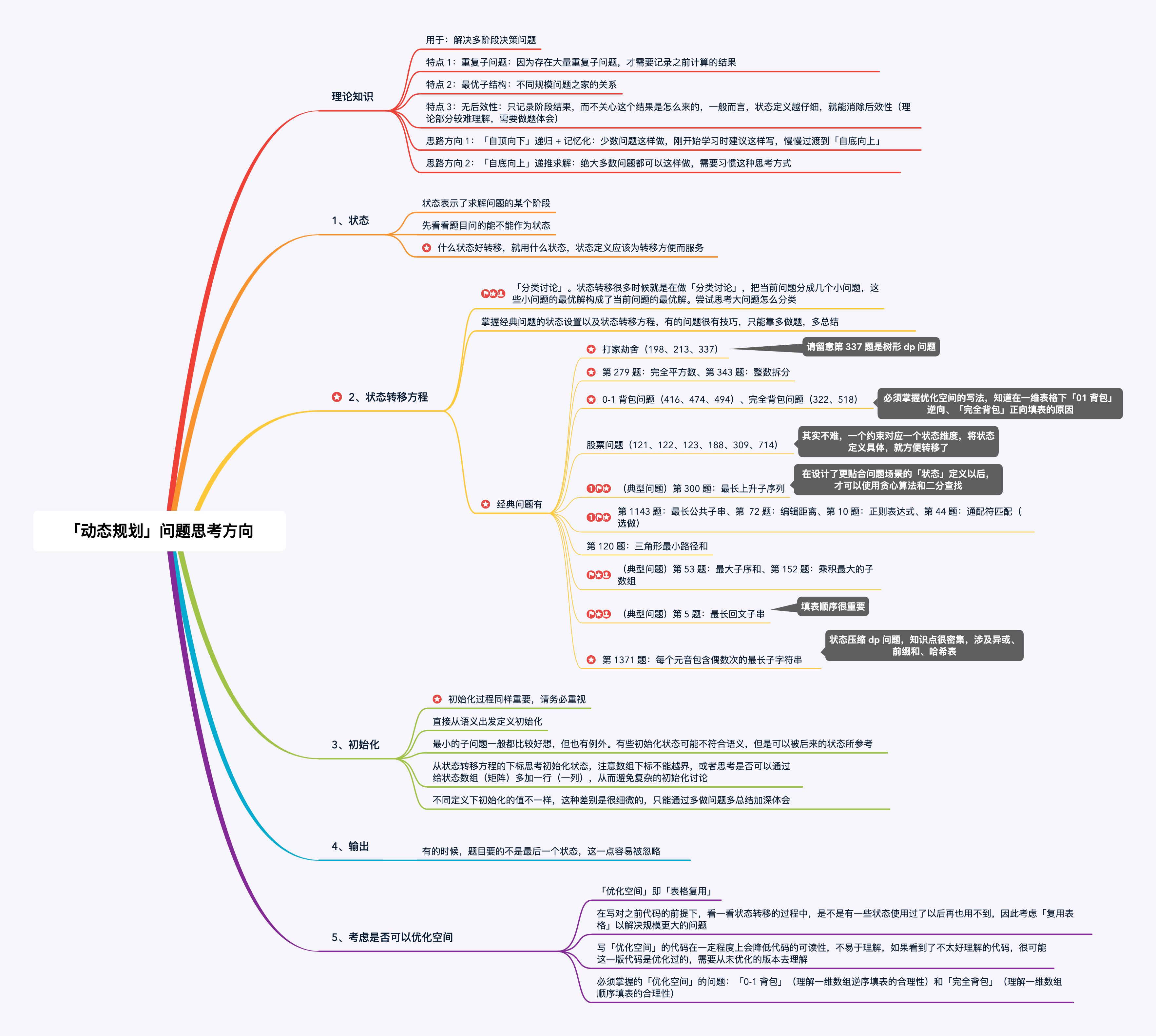
LeetCode53.最大子序和
滑动窗口法
虽然调了半天能AC,但面试这么写肯定挂:

class Solution {
public:
int maxSubArray(vector<int>& nums) {
vector<int> sum(nums.size(),0);
sum[0] = nums[0];
for(int i=1; i<nums.size(); i++){
sum[i] = sum[i-1] + nums[i];
}
int ans = sum[0];
// 用滑动窗口求出一段窗口之间的差值最大值
for(int i = 0; i<sum.size()-1; i++){
for(int j = i+1; j<sum.size(); j++){
if((sum[j]-sum[i])>ans)
ans = (sum[j]-sum[i]);
if(sum[j]>ans)
ans = sum[j];
}
}
return ans;
}
};动态规划解法
太经典了,据说是算法导论里的原题,留下了没读过算法导论的泪水……
动态维护两个最大值之和,当前最大和 和 总的数组最大和,其中总的数组最大和就是我们所要求的答案。扫描一遍,时间复杂度为O(N)。
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int sum = nums[0];
int maxsum = nums[0];
for(int i=1;i<nums.size();i++){
// 当前最大和,要么是之前的最大和加上当前的元素,
// 要么从当前的元素开始重新判断一段连续数组最大和
sum = max(sum+nums[i], nums[i]);
// 动态维护总的最大和
maxsum = max(maxsum,sum);
}
return maxsum;
}
};事后诸葛亮:这道题一开始用滑动窗口 前缀和这样的思路是完全正确的,因为题目的意思完全符合这种思路,事实证明用这种思路也能够AC;但是怎样会想到动态规划思想呢?可以观察到关键词:“最大”、“连续”,细品,再细品!这是不是动态规划的精髓字眼?是不是记忆化搜索的精髓思想?
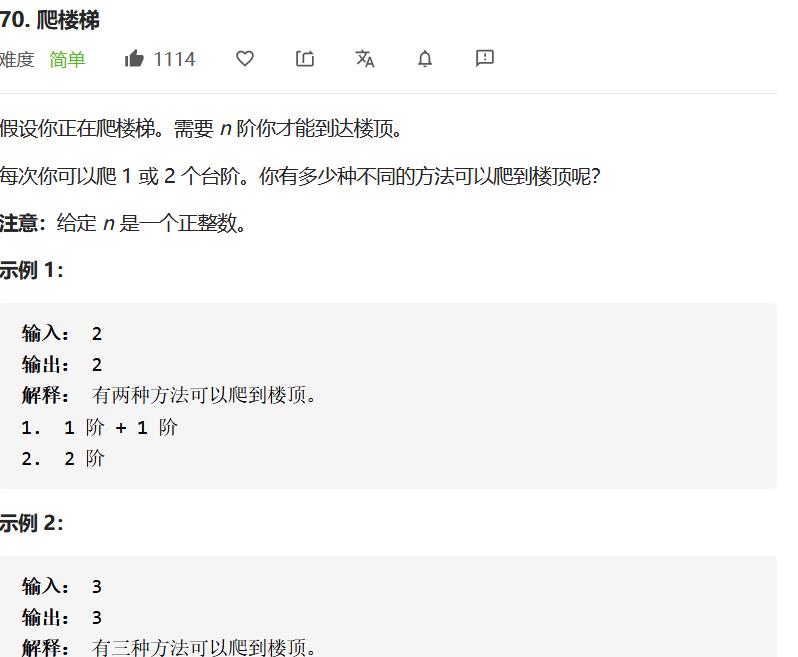
LeetCode70.爬楼梯
相信这道题是很多很多人的DP入门题,童年的回忆啊哈哈哈哈
class Solution {
public:
int climbStairs(int n) {
if(n<=2)
return n;
vector<int> dp(n+1,0);
dp[1] = 1;
dp[2] = 2;
for(int i=3;i<=n;i++){
dp[i] = dp[i-1]+dp[i-2];
}
return dp[n];
}
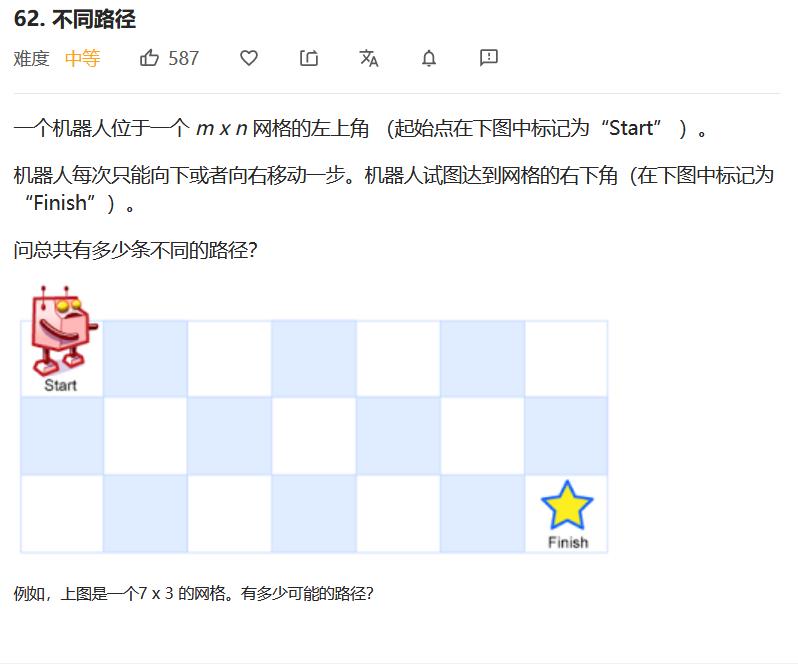
};经典入门级DP:LeetCode62.不同路径
超经典的一道DP入门题!
class Solution {
public:
int uniquePaths(int m, int n) {
// 代表当前节点所包含的路径总数
int dp[m][n];
// 初始化首行和首列
for (int i = 0; i<m; i++)
dp[i][0] = 1;
for (int j = 0; j<n; j++)
dp[0][j] = 1;
// 状态转移方程
for (int i = 1; i<m; i++)
for (int j = 1; j<n; j++)
dp[i][j] = dp[i-1][j] + dp[i][j-1];
return dp[m-1][n-1];
}
};有障碍物的不同路径:LeetCode.63.不同路径II
完全可以从上面这题受到启发,就是多了进行障碍物处理的步骤

class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
// dp[i][j]表示通向坐标i,j的路径总数
int dp[m][n];
// 进行初始化
int i;
for(i = 0; i<m; i++) {
if(obstacleGrid[i][0] != 0) // 遇到了无法到达的情况
break;
dp[i][0] = 1;
}
// 将无法达到的情况置零
while(i<m) {
dp[i][0] = 0;
i++;
}
int j;
for(j = 0; j<n; j++) {
if(obstacleGrid[0][j] != 0) // 遇到了无法到达的情况
break;
dp[0][j] = 1;
}
// 将无法到达的情况置零
while(j<n) {
dp[0][j] = 0;
j++;
}
// 状态转移方程
for(int i = 1; i<m; i++) {
for(int j = 1; j<n; j++) {
if(obstacleGrid[i][j] == 0) {
dp[i][j] = dp[i-1][j] + dp[i][j-1]; // 状态转移方程
} else { // 遇到障碍的情况,则此时是无法到达的
dp[i][j] = 0;
}
}
}
return dp[m-1][n-1];
}
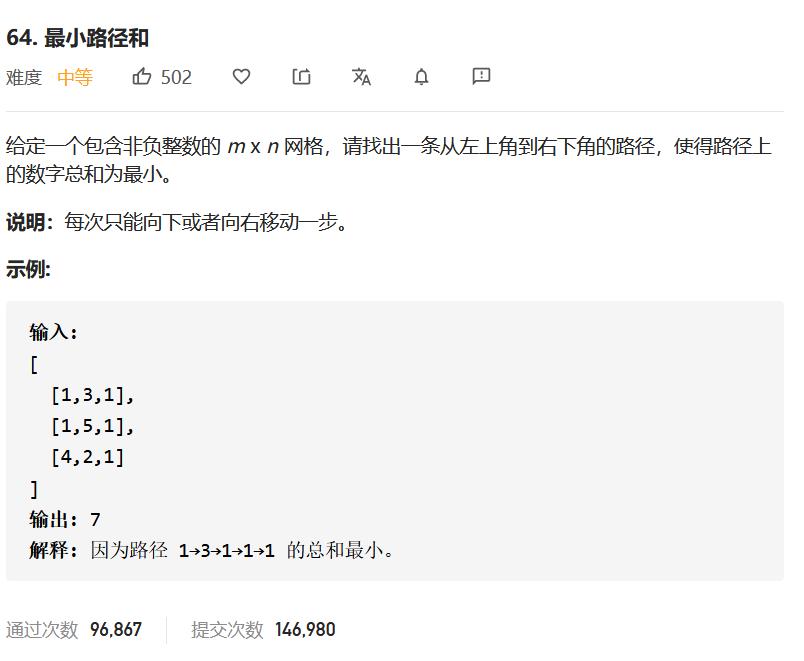
};DP记忆化搜索:LeetCode64.最小路径和
其实这道题和上面两题很相似,可以说是升级版本!
和下面这题找最大路径和可以说是套题哈哈
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int row = grid.size();
int col = grid[0].size();
int dp[row][col]; // dp[i][j]代表到达第i,j个空格所需要的最短路径
dp[0][0] = grid[0][0];
// 初始化
for(int i = 1; i<row; i++){
dp[i][0] = grid[i][0]+dp[i-1][0];
}
for(int j = 1; j<col; j++) {
dp[0][j] = dp[0][j-1]+grid[0][j];
}
// 贪心/DP寻找局部最优解
for (int i = 1; i<row; i++) {
for (int j = 1; j<col; j++) {
// 第i,j个空格的所需最短路径是左边一个空格最短路径和上边一个空格最短路径加上此空格的数字
dp[i][j] = min(dp[i][j-1],dp[i-1][j])+grid[i][j];
}
}
return dp[row-1][col-1];
}
};最大路径和:LeetCode剑指offer47.礼物的最大价值
这是一道超级经典的DP,建议先做62和63题,完全一个套路;
和64题相对应,把64题中最小路径改成最大路径即可!

class Solution {
public:
int maxValue(vector<vector<int>>& grid) {
// dp[i][j]表示(i,j)坐标下能拿到礼物的最大值
int dp[grid.size()][grid[0].size()];
dp[0][0] = grid[0][0];
// 初始化
for (int i = 1; i<grid.size(); i++)
dp[i][0] = grid[i][0] + dp[i-1][0];
for (int j = 1; j<grid[0].size(); j++)
dp[0][j] = grid[0][j] + dp[0][j-1];
// 贪心找局最优,总是沿着最大值的路径去走
for (int i = 1; i<grid.size(); i++)
for (int j = 1; j<grid[0].size(); j++)
dp[i][j] = max(dp[i-1][j], dp[i][j-1]) + grid[i][j];
return dp[grid.size()-1][grid[0].size()-1];
}
};经典入门级DP:LeetCode198.打家劫舍
这道题可以说是LeetCode上最经典,出镜率最高的问题之一,据说字节还叫头条的时候,动不动就出这道题来玩……
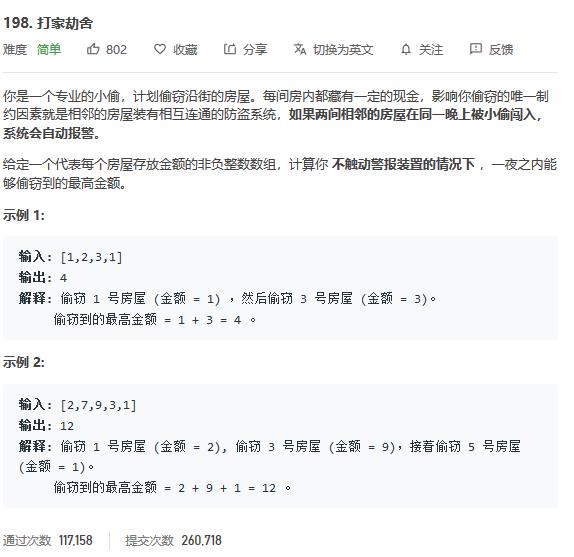
一开始完全没思路,尿了
看热评第一的大佬:

我只能说,大佬牛逼!!!
解释:
假设偷盗经过了第i个房间时,那么有两种可能,偷第i个房间,或不偷第i个房间。如果偷得话,那么第i-1的房间一定是不偷的,所以经过第I个房间的最大值DP(i)=DP(I-2) +nums[i];如果经过第i房间不偷的话,那么经过第i房间时,偷取的最大值就是偷取前i-1房价的最大值。
这两种方案分别是dp[i-2]+nums[i]和 dp[i-1],取最大值就是经过第i房间的最大值。

class Solution {
public:
int rob(vector<int>& nums) {
if (nums.empty())
return 0;
else if (nums.size() == 1)
return nums[0];
int dp[nums.size()];
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
for (int i = 2; i<nums.size(); i++) {
// 要么是上一次打劫(上上一家)得到的综合加上这这家打劫的金额
// 要么是从上面一家开始打劫,之前打劫的不算
dp[i] = max(dp[i-2] + nums[i], dp[i-1]);
}
return dp[nums.size()-1];
}
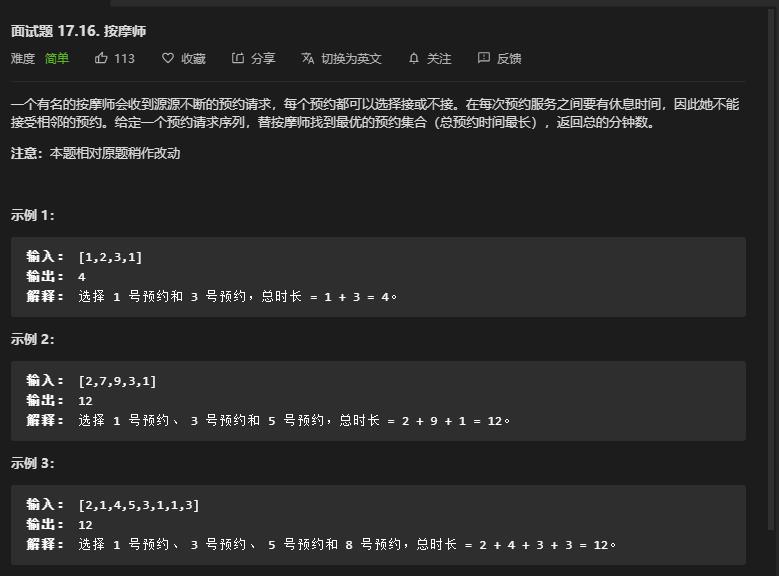
};从打劫犯到按摩技师:LeetCode面试题.17.16按摩师
从打劫犯人到按摩技师,都是我们无产阶级的敌人!
一样的题就当练习手速了,真香!
class Solution {
public:
int massage(vector<int>& nums) {
if (nums.empty())
return 0;
if (nums.size() == 1)
return nums[0];
int dp[nums.size()];
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
for (int i = 2; i<nums.size(); i++)
dp[i] = max(dp[i-2] + nums[i], dp[i-1]);
return dp[nums.size()-1];
}
};用贪心改善DP:LeetCode343.整数拆分&&面试题14-I.剪绳子
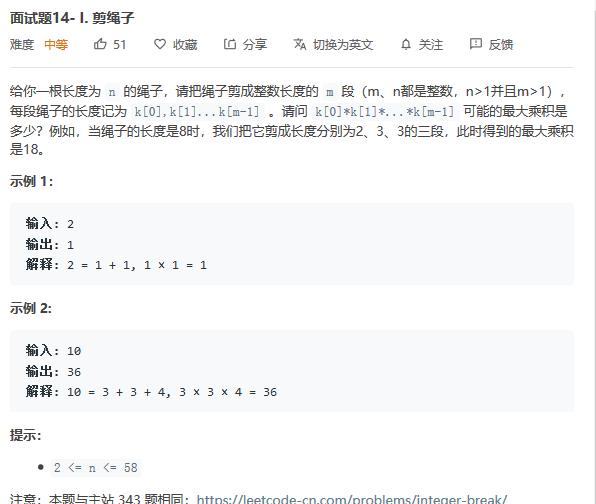
“以3为最优质因子的贪心法”:
相关证明会牵扯到比较深的数论问题,可以简单理解为以下:
- 任何大于1的数都可由2和3相加组成(根据奇偶证明)
- 因为2*2=1*4,2*3>1*5, 所以将数字拆成2和3,能得到的积最大
- 因为2*2*2<3*3, 所以3越多积越大 时间复杂度O(n/3),用幂函数可以达到O(log(n/3)), 因为n不大,所以提升意义不大,我就没用。 空间复杂度常数复杂度O(1)

class Solution {
public:
int cuttingRope(int n) {
if(n<=3)
return n-1;
int sum = 1;
// 将绳子分成多个长度为3的片段,在与留下绳子的长度相乘
while(n>4){
sum*=3;
n-=3;
}
return sum*n;
}
};动态规划法:
心情如上,用DP写比较复杂,好吧,其实是我不会,溜了
以上是关于经典动态规划——从LeetCode题海中总结常见套路的主要内容,如果未能解决你的问题,请参考以下文章