数据结构和算法衡量算法的标尺,时间和空间复杂度详解
Posted Linux猿
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构和算法衡量算法的标尺,时间和空间复杂度详解相关的知识,希望对你有一定的参考价值。
🎈 作者:Linux猿
🎈 简介:CSDN博客专家🏆,华为云享专家🏆,Linux、C/C++、面试、刷题、算法尽管咨询我,关注我,有问题私聊!
🎈 关注专栏:动图讲解数据结构和算法 (优质好文持续更新中……)🚀
🎈 欢迎小伙伴们点赞👍、收藏⭐、留言💬
目录

【百日实战】计划开始啦!接下来 100 天的时间,会针对 【数据结构和算法】 出一个 系列,目标是将基础数据结构和算法讲易、讲精、讲通,本系列的文章将从实战的角度出发,进行讲解,下面这些情况都适合:
(1)正在面试的小伙伴;
(2)正在学习数据结构和算法的小伙伴;
(3)正在复习考研数据结构和算法的小伙伴;
(4)日常学习数据结构和算法的小伙伴;
都可以跟着系列走(记得关注专栏动图讲解数据结构和算法哦!)

下面是知识点结构图,如下所示:
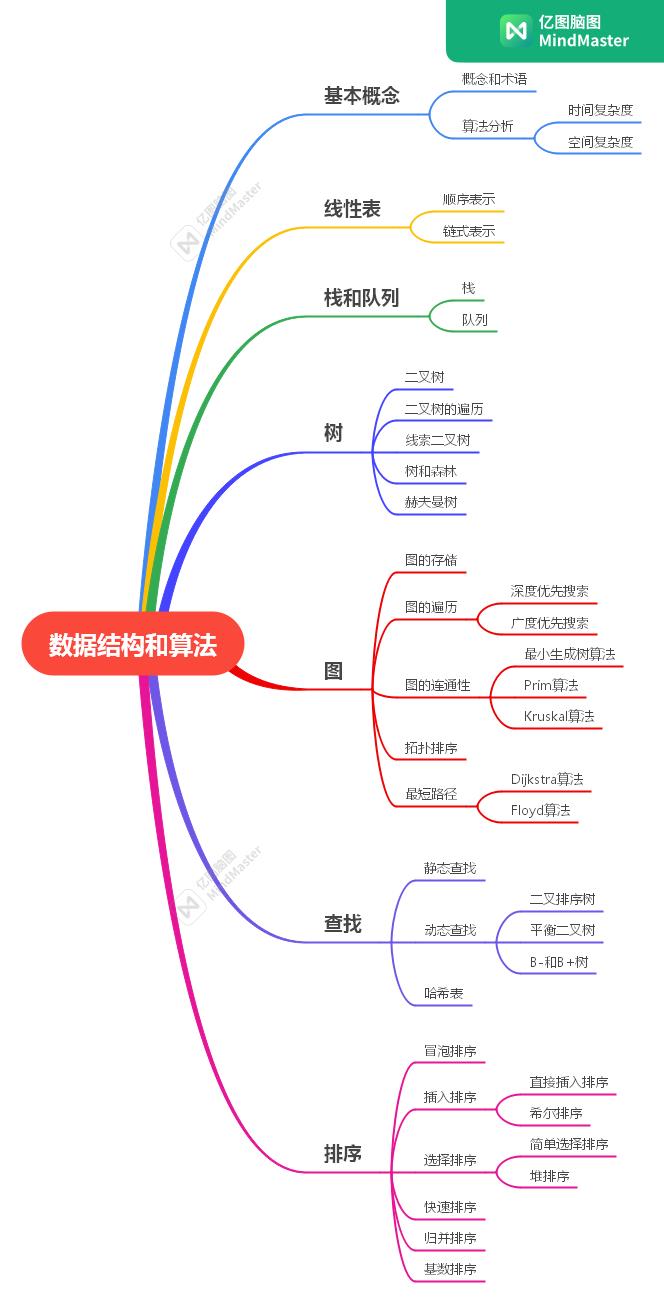
下面就开始吧!

对于一个问题,存在着许多解题方法,那如何评价方法的优劣呢?通常来说会考虑算法的时间复杂度和空间复杂度。下面就为大家介绍下算法的时间和空间复杂度。
🔶🔶🔶🔶🔶 我是分割线 🔶🔶🔶🔶🔶
🍓一、什么是时间复杂度 ?
咱们先从字面意思来理解下,时间复杂度无非就是算法解决一个问题所需要的运行时间。这样说你可能理解了,但是,好像没有完全理解。

你没说咋计算呀!重点是 如何计算时间复杂度 ?
别急,下面马上就来说。
计算时间复杂度最重要的是理解这个概念:基本操作,例如:执行一次 for 循环,执行一条语句等。
好了,下面来理解下面这句话:
一般情况下,算法中 基本操作 重复执行的次数是问题规模 n 的某个函数 f(n),算法的时间量度记作:
T(n) = O(f(n))
上述公式表示随问题规模 n 的增大,算法执行时间的增长率和 f(n) 的增长率相同,称做算法的渐近时间复杂度,简称时间复杂度。
从定义可以看出,算法中基本操作重复执行的次数与算法的时间复杂度的大小成正比,因此重点是计算算法中基本操作重复执行的次数。
🔶🔶🔶🔶🔶 我是分割线 🔶🔶🔶🔶🔶
🍓二、什么是空间复杂度?
算法运行所需的存储空间称为空间复杂度,记作:
S(n) = O(f(n))
其中,n 为问题的规模(或大小)。算法的空间复杂度考虑的是除 输入和程序 之外的额外空间。上面这句话一定要理解,换言之,空间复杂度计算的是算法运行过程中使用的临时空间。
空间复杂度特别要注意递归算法的空间复杂度(例如:深度优先搜索),递归算法的空间复杂度相当于额外增加了一个栈空间来存储函数递归的信息。例如:快速排序的空间复杂度为O(logn),即递归的层次。
除了栈空间外,更多的是考虑额外申请的数组增加的空间复杂度,例如:归并排序中,在进行归并的时候,额外需要一个数组空间进行操作。
🍓三、常见时间复杂度分析
✨3.1 常量阶 O(1)
常量阶通常是没有复杂算法的顺序执行,相对于规模 n 来说是常量级的,这里 f(n) 和 n 的关系为:
f(n) = b (b 是一个常数)
下面来看一个例子,计算 1 + 2 + 3 + …… + n 的和。
先来看下复杂度为 O(n) 的算法:
#include <iostream>
using namespace std;
int main()
{
int n;
while(cin>>n) {
int sum = 0;
for(int i = 1; i <= n; ++i) { // for 循环
sum += i;
}
cout<<"sum = "<<sum<<endl;
}
return 0;
}下面来看下 O(1) 的时间复杂度:
#include <iostream>
using namespace std;
int main()
{
int n;
while(cin>>n) {
cout<<"sum = "<<(1+n)*n/2<<endl;
}
return 0;
}很明显,第一个例子中需要一个 for 循环来求和,for 循环执行 n 次,所以复杂度为 O(n),第二个例子只需要计算一次即可,所以复杂度为 O(1)。
下面再来看下计算圆的周长和面积的例子:
#include <iostream>
using namespace std;
#define PI 3.1415
int main()
{
double r;
while(cin>>r) {
double s = PI * r * r;
double c = 2 * PI * r;
cout<<"The area of the circle is "<<s<<endl;
cout<<"The circumference of the circle is "<<c<<endl;
}
return 0;
}上述例子中,每次输入半径 r,然后,计算圆的周长和面积。
例子中都是基本的程序执行操作,语句执行次数没有达到一定规模,可以看做是常数阶的复杂度。
✨3.2 对数阶O(logn)
对数阶,常见的是 O(logn) 的对数阶复杂度,f(n) 和 规模 n 的关系为:
2^f(n) = n
f(n) = 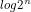
下面来看一个例子,二分查找算法代码如下所示:
/*
* 二分查找
* A[] : 待查找的数组
* n : 数组长度
* target : 查找的目标值
*/
int binarySearch(int A[], int n, int target) {
int lt = 0, rt = n;
while(lt < rt){
int mid = lt + (rt - lt)/2;
if(A[mid] == target) return mid;
else if(A[mid] > target) rt = mid;
else lt = mid + 1;
}
return -1; // 查找不到
}二分查找算法每次排除一半的元素,相当于每次在规模 n 的基础上除以 2,所以时间复杂度为 O(logn)。
✨3.3 线性阶 O(n)
线性阶是指随着规模 n 的增长,复杂度也是线性增长,f(n) 和 规模 n 的关系为:
f(n) = a* n + b (a 和 b 为 常数)
下面来看一个例子,输入 n 个数,计算输入的 n 个数的和,如下所示:
#include <iostream>
using namespace std;
int main() {
int n;
while(cin>>n) {
int sum = 0, num;
for(int i = 0; i < n; ++i) {
cin>>num;
sum += num;
}
cout<<"The sum is "<<sum<<endl;
}
return 0;
}上例中,计算时间复杂度主要是看 for 循环,一次 for 循环可以看做一个基本操作,需要执行 n 次 for 循环,所以时间复杂度为 O(n)。
看了上面的例子后,有的小伙伴可能就说了,看见单个 for 循环就是 O(n) 的复杂度!

下面就来看一个反例,如下所示:
int function(int n) {
int sum = 0;
for (int i = 2; i < n; i *= 2) {
sum += i;
}
return sum;
}
上例中,2^f(n) = n,f(n) = log2^n,所以时间复杂度为 O(log2^n),并不是 O(n)。
✨3.4 平方阶 O(n^2)
平方阶是指时间复杂度是规模 n 的平方,规模 n 和 f(n) 的关系为:
f(n) = n^2
来看一个例子,下面是冒泡排序算法,时间复杂度为O(n^2)。
#include <iostream>
using namespace std;
#define SIZE 1000
int main() {
int n;
int a[SIZE];
while(cin>>n) {
for(int i = 0; i < n; ++i) {
cin>>a[i];
}
// 冒泡排序
for(int i = 0; i < n - 1; ++i) {
for(int j = 0; j < n - i - 1; ++j) {
if(a[j] > a[j+1]) {
swap(a[j], a[j+1]);
}
}
}
for(int i = 0; i < n; ++i) {
cout<<a[i]<<" ";
}
cout<<endl;
}
return 0;
}在上述代码中,时间复杂度主要在冒泡排序上,所以时间复杂度为 O(n^2)。
✨3.5 指数阶 O(2^n)
指数阶,这里以 O(2^n) 为例进行说明,通常指数阶的算法不常见,因为随着 n 的增大,复杂度呈指数增长,f(n) 和 规模 n 的关系为:
f(n) = 2^n
下面来看一个例子,计算斐波那契数列,如下所示:
long fibonacci(int n) {
if (n <= 1) {
return 1;
} else {
return fibonacci(n - 1) + fibonacci(n - 2);
}
}斐波那契数列的公式为:
F(n) = F(n - 1) + F(n - 2) (n > 2)
时间复杂度经过计算后为 O(2^n)(这里的时间复杂度为上述代码中递归算法的时间复杂度)。
🔶🔶🔶🔶🔶 我是分割线 🔶🔶🔶🔶🔶
🍓四、常见空间复杂度分析
空间复杂度没有时间复杂度那么受到重视,在日常的算法中,可能优先考虑的是时间复杂度,因为一些算法的空间并不受限,在一些嵌入式领域可能空间复杂度更重要一点。
✨4.1 O(1)
实质上,很多算法的空间复杂度为 O(1),比如:冒泡排序、简单选择排序、插入排序等。
✨4.2 O(n)
还是拿排序来举例,归并排序的空间复杂度为 O(n)。
为什么很多排序算法都是 O(1) ,归并排序确是 O(n) 呢 ?

先来看下归并排序的代码,如下所示:
/*
* 归并排序
* 其中, p[]是一个临时数组,存储排序元素
*/
// 合并
void merge(int a[], int lt, int rt, int p[]){
int mid = (rt - lt)/2 + lt;
int i = lt, j = mid + 1;
int k = 0;
while(i <= mid && j <= rt){ // 合并
if(a[i] <= a[j]){
p[k++] = a[i++];
}else {
p[k++] = a[j++];
}
}
while(i <= mid){ // 合并剩余的
p[k++] = a[i++];
}
while(j <= rt){ // 合并剩余的
p[k++] = a[j++];
}
for(i = 0; i < k; ++i){ // 重新赋值回去
a[lt+i] = p[i];
}
}
// 划分
void mergeSort(int a[], int lt, int rt, int p[]){
if(lt < rt){
int mid = (rt - lt)/2 + lt;
mergeSort(a, lt, mid, p); // 递归排序 lt ~ mid
mergeSort(a, mid+1, rt, p); // 递归排序 mid+1 ~ rt
merge(a, lt, rt, p); // 合并 lt ~ rt
}
}在上述的归并排序中,主要的空间复杂度在于 p[] 数组那,p[] 数组长度为 n,用于暂存合并后的元素,所以空间复杂度为 O(n)。
✨4.3 O(logn)
说到 O(logn) 的空间复杂度,可能一下想不出来。递归写法的快速排序在最好的情况下(正好每次都二分)空间复杂度为 O(logn),因为每次都是二分,故递归的层次为 logn,而每次递归会让栈空间增加一层,所有空间复杂度为 O(logn)。
🔶🔶🔶🔶🔶 我是分割线 🔶🔶🔶🔶🔶
🍓五、总结
上面对时间和空间复杂度进行了说明,并列出了常见的时间和空间复杂度,当然,还有更复杂的,有的甚至需要列公式推算一下,本文不再列出。
后续还将更新更多更优质的 数据结构和算法 好文,赶紧点击(动图讲解数据结构和算法)订阅专栏吧!
如果本文对你有帮助,欢迎小伙伴们点赞👍、收藏⭐、留言💬

欢迎关注下方👇👇👇公众号👇👇👇,获取更多优质内容🤞(比心)!
以上是关于数据结构和算法衡量算法的标尺,时间和空间复杂度详解的主要内容,如果未能解决你的问题,请参考以下文章