图论最短路径问题（图的绘制以及Dijkstra算法和Bellman‐Ford算法）

Posted 2021-12-03 衾许°

1.作图代码：均为MATLAB语法

% 函数graph(s,t)：可在 s 和 t 中的对应节点之间创建边，并生成一个图

• G1 = graph(s1, t1);                %图矩阵的生成，并通过该图矩阵生成图
• plot(G1);                                %打印G1图

 小例子1：生成一个权值均为1的无向图

• s1 = [1,2,3,4];
• t1 = [2,3,1,1];
• %1节点与2节点相连，2节点与3节点相连，3节点与1节点相连，4节点与1节点相连
• G1 = graph(s1, t1);
• plot(G1)

生成图像如下

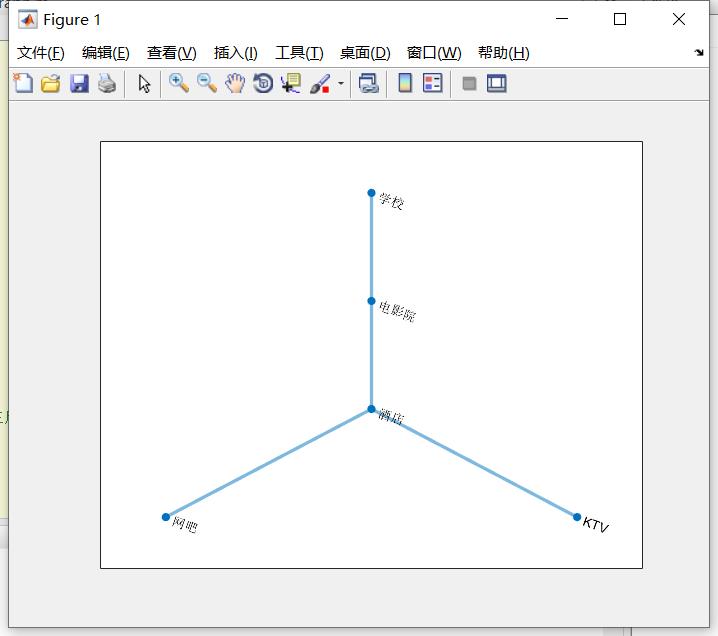
小例子2：还可以以文字作为节点名进行图的绘制

• s2 = {'学校','电影院','网吧','酒店'};
• t2 = {'电影院','酒店','酒店','KTV'};
• G2 = graph(s2, t2);
• plot(G2, 'linewidth', 2)  % 设置线的宽度
• % 下面的命令是在画图后不显示坐标
• set( gca, 'XTick', [], 'YTick', [] );

执行后如下

小例子3：:权重不只是为1的无向图

• % 函数graph(s,t,w)：可在 s 和 t 中的对应节点之间以w的权重创建边，并生成一个图
• s = [1,2,3,4];
• t = [2,3,1,1];
• w = [3,8,9,2];
• G = graph(s, t, w);
• plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2) %设置线宽和图像宽窄
• set( gca, 'XTick', [], 'YTick', [] );  %无坐标轴

执行后图像如下：

小例子4：:权值为1有向图
无权图： digraph(s,t)

• s = [1,2,3,4,1];
• t = [2,3,1,1,4];
• G = digraph(s, t);
• plot(G)
• set( gca, 'XTick', [], 'YTick', [] );  

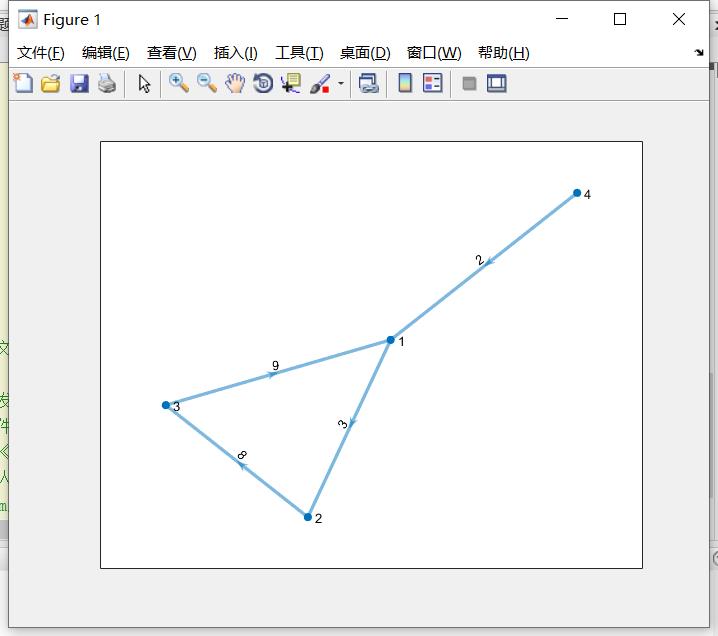
小例子5.有向权值不为1图

digraph(s,t,w)

• s = [1,2,3,4];
• t = [2,3,1,1];
• w = [3,8,9,2];
• G = digraph(s, t, w);
• plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2) 
• set( gca, 'XTick', [], 'YTick', [] ); 

 2.两种最短路径的算法代码

% 注意哦，Matlab中的图节点要从1开始编号，所以这里把0全部改为了9
% 编号最好是从1开始连续编号，不要自己随便定义编号

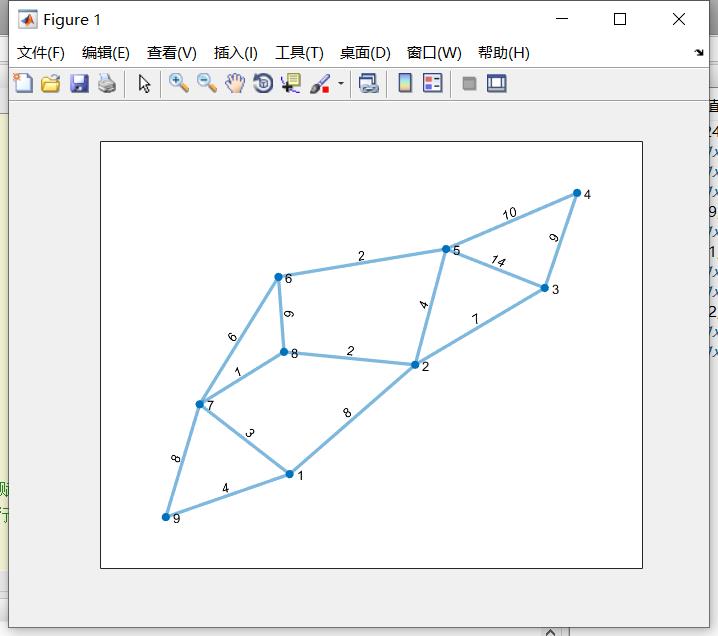
• s = [9 9 1 1 2 2 2 7 7 6 6  5  5 4];
• t = [1 7 7 2 8 3 5 8 6 8 5  3  4 3];
• w = [4 8 3 8 2 7 4 1 6 6 2 14 10 9];
• G = graph(s,t,w);
• plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2) 
• set( gca, 'XTick', [], 'YTick', [] );  %执行后如下图

• %最短路径求解函数
• %pram1为求解图，pram2为起点，pram3为终点

• [P,d] = shortestpath(G, 9, 4) 

• P =

       9     1     7     8     2     5     4%P输出为最短路径所经过的节点

  
  d =

      24%最短距离总共为24

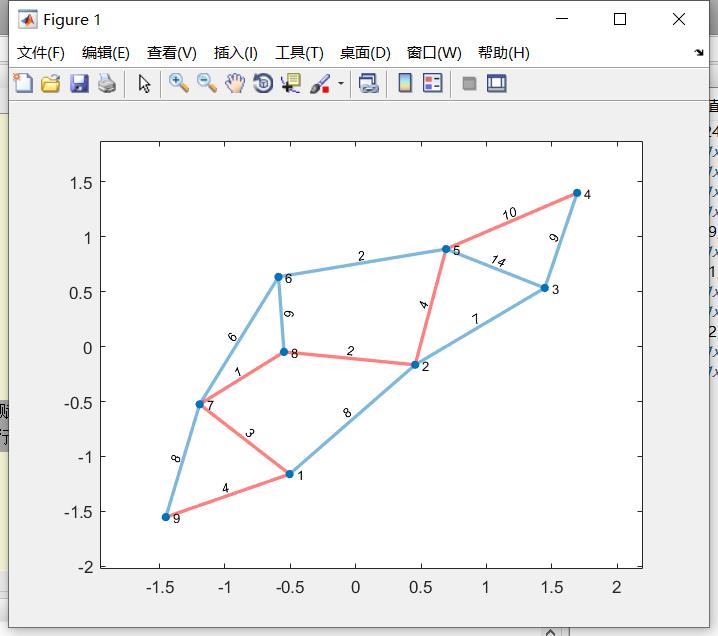
% 在图中高亮我们的最短路径

• myplot = plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2);  %首先将图赋给一个变量
• highlight(myplot, P, 'EdgeColor', 'r')   %对这个变量即我们刚刚绘制的图形进行高亮处理（给边加上r红色）

% 求出任意两点的最短路径矩阵

• D = distances(G)   %注意：该函数matlab2015b之后才有哦
• D(1,2)  % 1 -> 2的最短路径（第一行第二列）
• D(9,4)  % 9 -> 4的最短路径（第九行第四列）

D =

     0     6    13    20    10     9     3     4     4
     6     0     7    14     4     6     3     2    10
    13     7     0     9    11    13    10     9    17
    20    14     9     0    10    12    17    16    24
    10     4    11    10     0     2     7     6    14
     9     6    13    12     2     0     6     6    13
     3     3    10    17     7     6     0     1     7
     4     2     9    16     6     6     1     0     8
     4    10    17    24    14    13     7     8     0

ans =

     6

ans =

    24
 

% 找出给定范围内的所有点  nearest(G,s,d)
% 返回图形 G 中与节点 s 的距离在 d 之内的所有节点

• [nodeIDs,dist] = nearest(G, 2, 10)   %注意：该函数matlab2016a之后才有哦

nodeIDs =

     8
     7
     5
     1
     6
     3
     9

dist =

     2
     3
     4
     6
     6
     7
    10

 例题作业：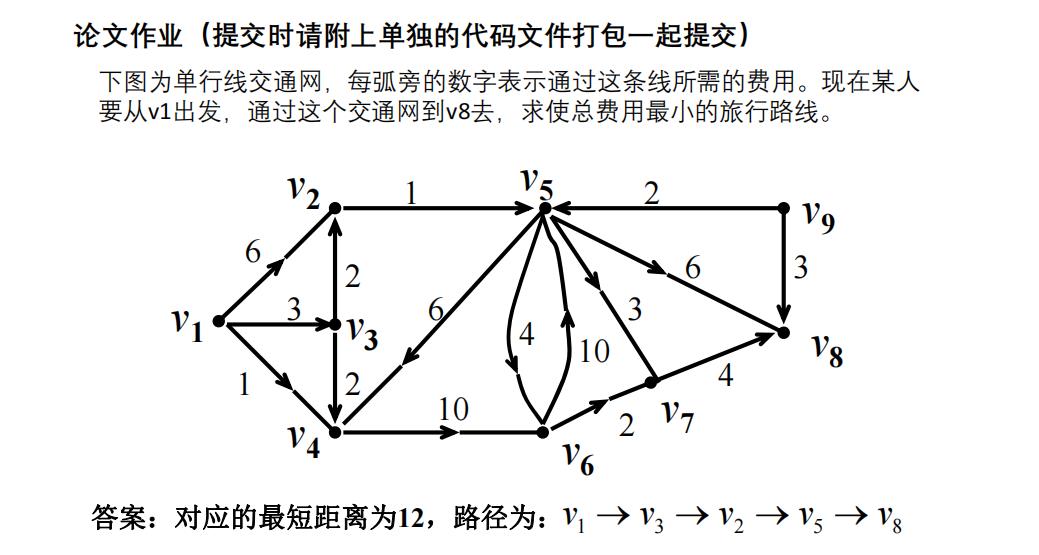

 其实这题也就很简单对吧？就是个最短路径问题，直接套用之前的代码，有向权值图

• s = [1,1,1,2,3,3,4,5,5,5,5,6,6,7,9,9];
• t = [2,3,4,5,2,4,6,4,6,7,8,7,5,8,8,5];
• w = [6,3,1,1,2,2,10,6,4,3,6,2,10,4,3,2];
• G = digraph(s, t, w);
• plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2)
• set( gca, 'XTick', [], 'YTick', [] );
• [P,d] = shortestpath(G, 1, 8)
• myplot = plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2); 
• highlight(myplot, P, 'EdgeColor', 'r') 

执行得

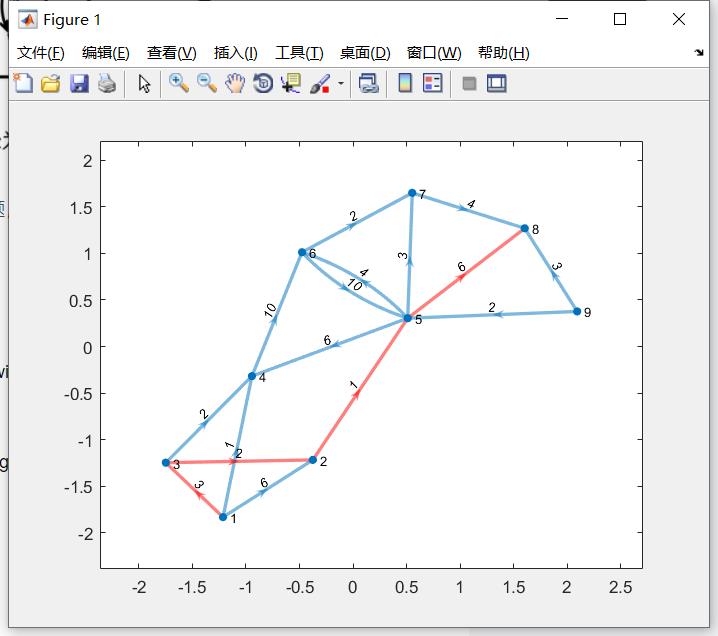
 P =

     1     3     2     5     8

d =

    12

 就这样，一个最短路径的问题作图以及算法运用就这样结束，告一段落好吧，虽然图论好像比较少题目会用到，但还是弄一弄吧，免得到时候比赛遇到了呢？