深入了解快排 以及 优化

Posted 鸢也

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了深入了解快排 以及 优化相关的知识，希望对你有一定的参考价值。

快排

文章目录


🎈🎆🎇 前言：

快排可以说是在排序中的地位重中之重，不仅在七大排序中速度快，而且也是面试官经常考的排序，也是数据结构中必须掌握的排序

🍕🍔🍟快速排序：

快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略，通常称其为分治法(Divide-and-ConquerMethod)。

🚗🚓🚕基本思想：

1、从待排序区间选择一个数作为基准值；

2、遍历这个待排序区间，比基准值小的放基准值得左边，比基准值大的放在右边；

3、采用分治思想，当left和right相遇的时候，就可以分为左右两个区间，

4、按照第2点同样的方式进行遍历，递归，直到各小区间长度==1，代表有序，长度是0，代表没有数据。

做题常见选基准值方法有：

  • 挖坑法；

  • Hoare 法；

下面找基准的方法是对快排的优化：

  • 随机选择；

  • 三数取中；

  • 直接插入排序

一、挖坑法

☮✝☪思路：

最开始设start为基准值，放在tmp中，然后比较大小，比基准值小的放基准值得左边，比基准值大的放在右边，如果end比tmp大就–，直到找到比tmp小的值交换，start同理，比tmp小小就++，直到找到比tmp大的值交换。

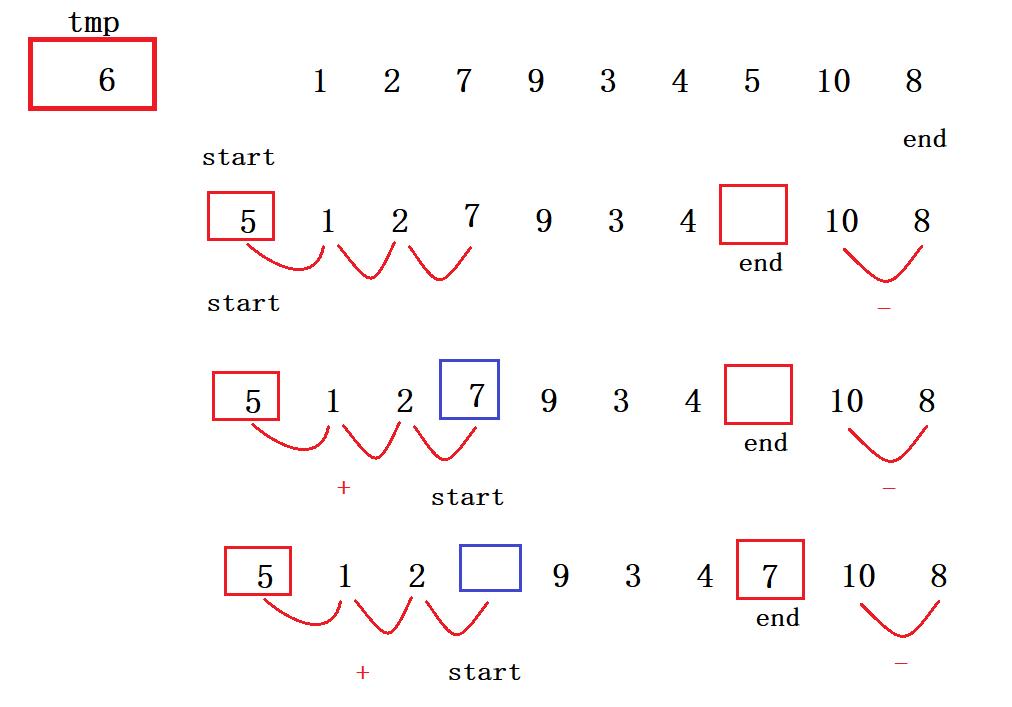
🍳🧇🥞代码：

public static int partition(int[] array,int start,int end) {
        int tmp=array[start];
        while(start<end) {
            //start<end 防止有序数组的时候end超过start  例如：1 2 3 4 5 6
            while(start<end && array[end]>=tmp) {//必须取等号，不然会无限循环
                end--;
            }
            array[start]=array[end];
            while (start<end && array[start]<=tmp) {
                start++;
            }
            array[end]=array[start];
        }
    //最后start和end相遇，使数组一分为二，完成分治思想
        array[start]=tmp;
        return start;
    }

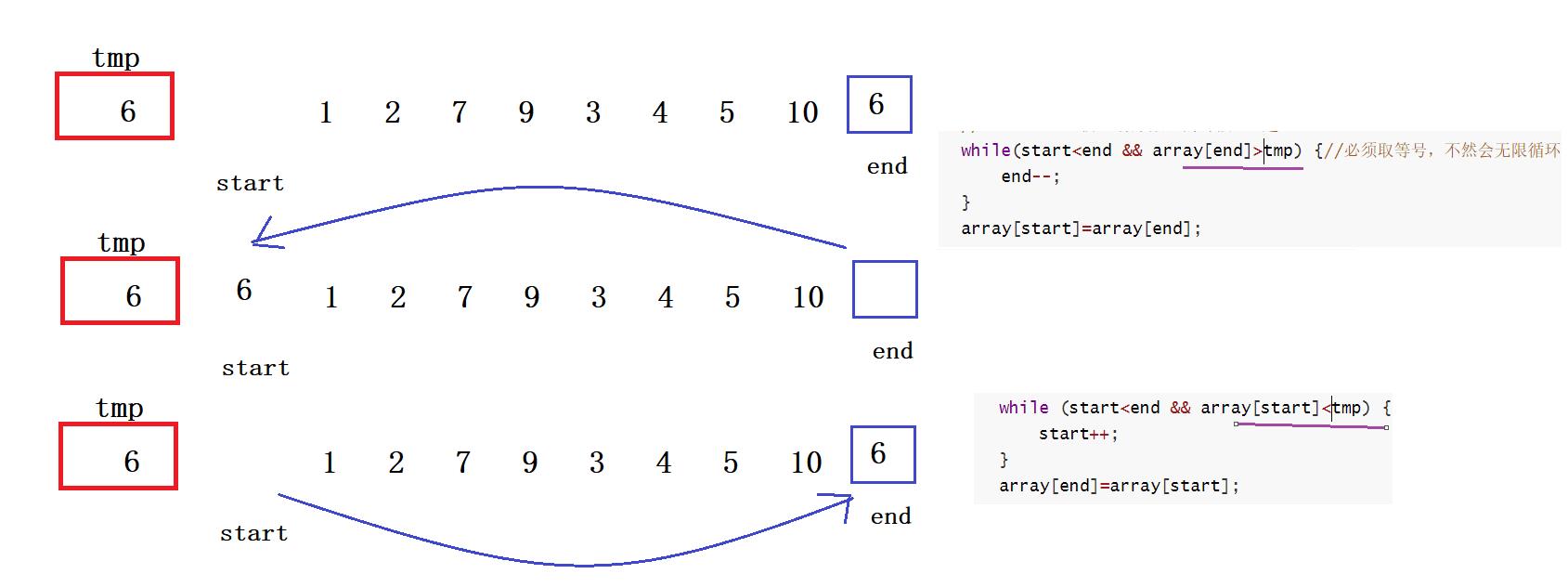
注意，一定要加上“=”不然会死循环

🍖🍗🥩完整代码：

public static int partition(int[] array,int start,int end) {
        int tmp=array[start];
        while(start<end) {
            while(start<end && array[end]>=tmp) {
                end--;
            }
            array[start]=array[end];
            while (start<end && array[start]<=tmp) {
                start++;
            }
            array[end]=array[start];
        }
        array[start]=tmp;
        return start;
    }

    //待排序区间
    public static void quick(int[] array,int left,int right) {
        if(left>=right) {
            return;
        }
        int pivot=partition(array,left,right);
        //递归 直到各小区间长度==1，代表有序，长度是0，代表没有数据。
        quick(array,left,pivot-1);
        quick(array,pivot+1,right);
    }

    public static void quickSo(int[] array) {
        quick(array,0,array.length-1);
    }

1.1 性能

时间复杂度：O(n*logn)

空间复杂度：O(logn)

稳定些：不稳定

二、Hoare法：

Hoare法思想其实跟挖坑法没有什么区别，都很好理解，

🍘🍙🍚思路：

最开始设start为基准值，放在tmp中，然后比较大小,同时找到last比基准值小的，begin比基准值大，他两进行交换，最后begin和last相遇的值再跟start进行交换。

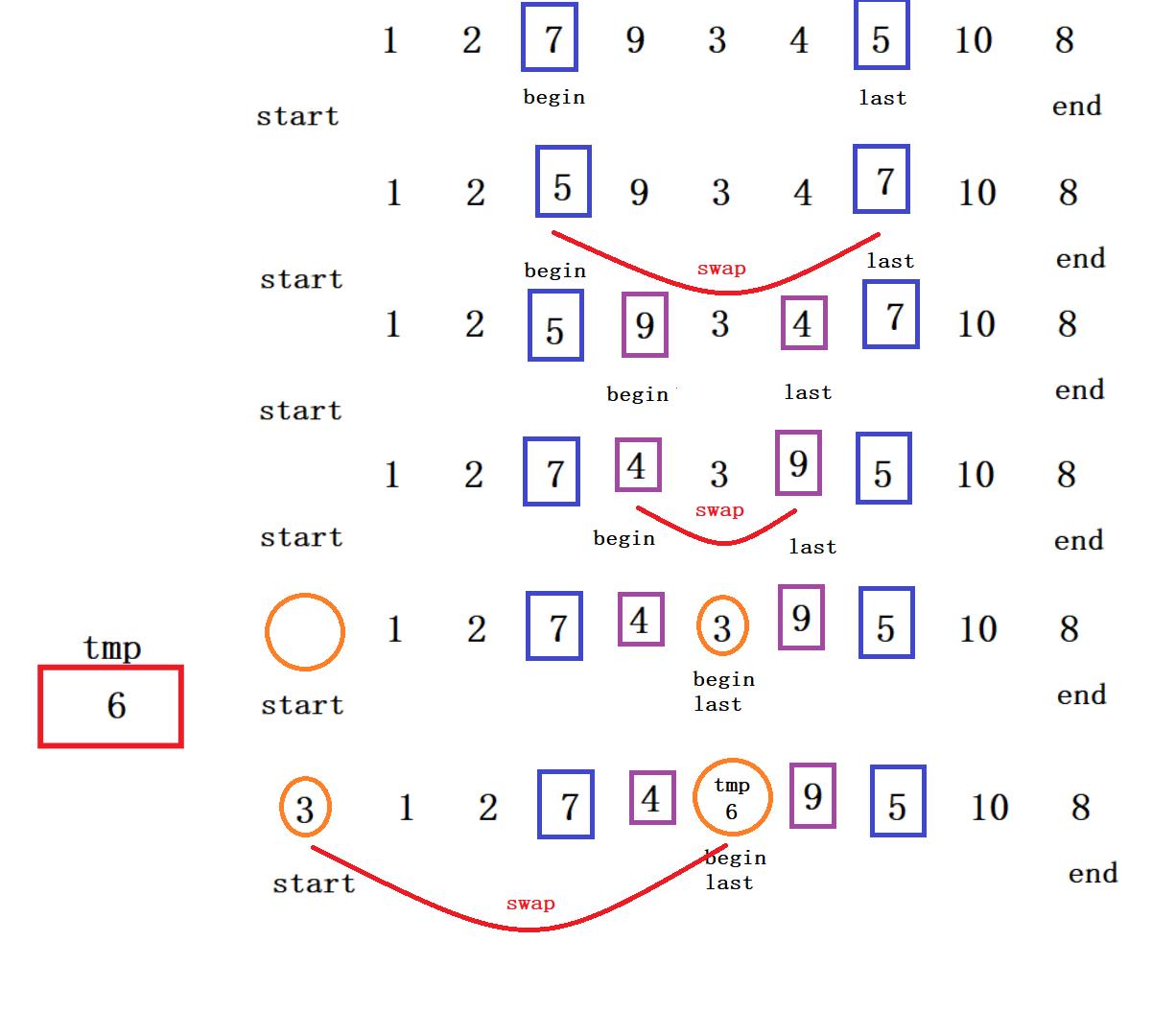
🧚‍♀️🧚‍♂️🤹‍♀️核心代码：

 public static int parentition2(int[] array,int start,int end) {
        int begin=start;
        int last=end;
        int tmp=array[start];
        while (begin<last) {
            while (begin<last && array[last]>=tmp) {
                last--;
            }
            while (begin<last && array[begin]<=tmp) {
                begin++;
            }
            swap(array,begin,last);
        }
        swap(array,begin,start);
        return begin;
    }

一般情况下，做题通常用的是挖坑法，例如选择题；

那么当数据有序的情况下，快速排序的时间复杂度会变成O(n^2),空间复杂度O(n)，这也是最坏的情况下，所以引出了快速排序的优化。

三、三数取中法

快速排序的思想就是分而治制，在有序的数据中如果每次将待排序的的序列均匀的分割，时间复杂度就会更快；

🦪🍣🍤三数取中思路：

取中就是这一组数据中找到中间值，使中间值作为基准，进行分治；

条件为array[mid] <= array[left] <= array[right]

🍰🎂🍪核心代码：

public static void medianOfThree (int[] array,int left,int right) {
        int mid=(left+right)/2;
        if(array[mid]>array[left]) {
            int tmp=array[mid];
            array[mid]=array[left];
            array[left]=tmp;
        }
        if(array[left]>array[right]) {
            int tmp=array[left];
            array[left]=array[right];
            array[right]=tmp;

        }
        if(array[mid]>array[right]) {
            int tmp=array[mid];
            array[mid]=array[right];
            array[right]=tmp;
        }
    }

四、 随机选择

也是为了防止有序数组，采用在待排序列中任意取里面的元素作为基准；

🍵🧉🍶核心代码：

 public static void pivotRandow(int[] array,int left,int right) {
        //随机选择法
        Random random=new Random();
        int rand=random.nextInt(right-left)+left+1;
        int tmp=array[left];
        array[left]=array[rand];
        array[rand]=tmp;
    }

五、直接插入排序优化

一组数据越有序，那么直接插入排序是最快的，快排递归到某一个区间的时候会逐渐有序，我们就可以采用直接插入排序来优化

public static void quick(int[] array,int left,int right) {
        if(left>=right) {
            return;
        }
        int pivot=parentition2(array,left,right);

        //执行到一个区间之后  进行直接插入排序会更快
        if((right - left + 1) <= 100) {
            insertSort(array,left,right);
            return;
        }
        medianOfThree(array,left,right);
        //递归
        quick(array,left,pivot-1);
        quick(array,pivot+1,right);
    }

六、非递归快排

非递归快排比递归要麻烦点，分析的过程也要繁琐一点，但是有了前面挖坑法，Hoare法的基础也可以好理解；

🥂🥃🥤基本思路：

首先我们还是分治思想和前面的pivot一样，然后我们需要一个栈，pivot是一个基准，就各自分为两组待排序区间，在栈中放入开始和结束的下标，两个一组弹出，再跟上一步操作一样找基准点，相遇过后，又放入栈中，重复找基准点，直到完成排序

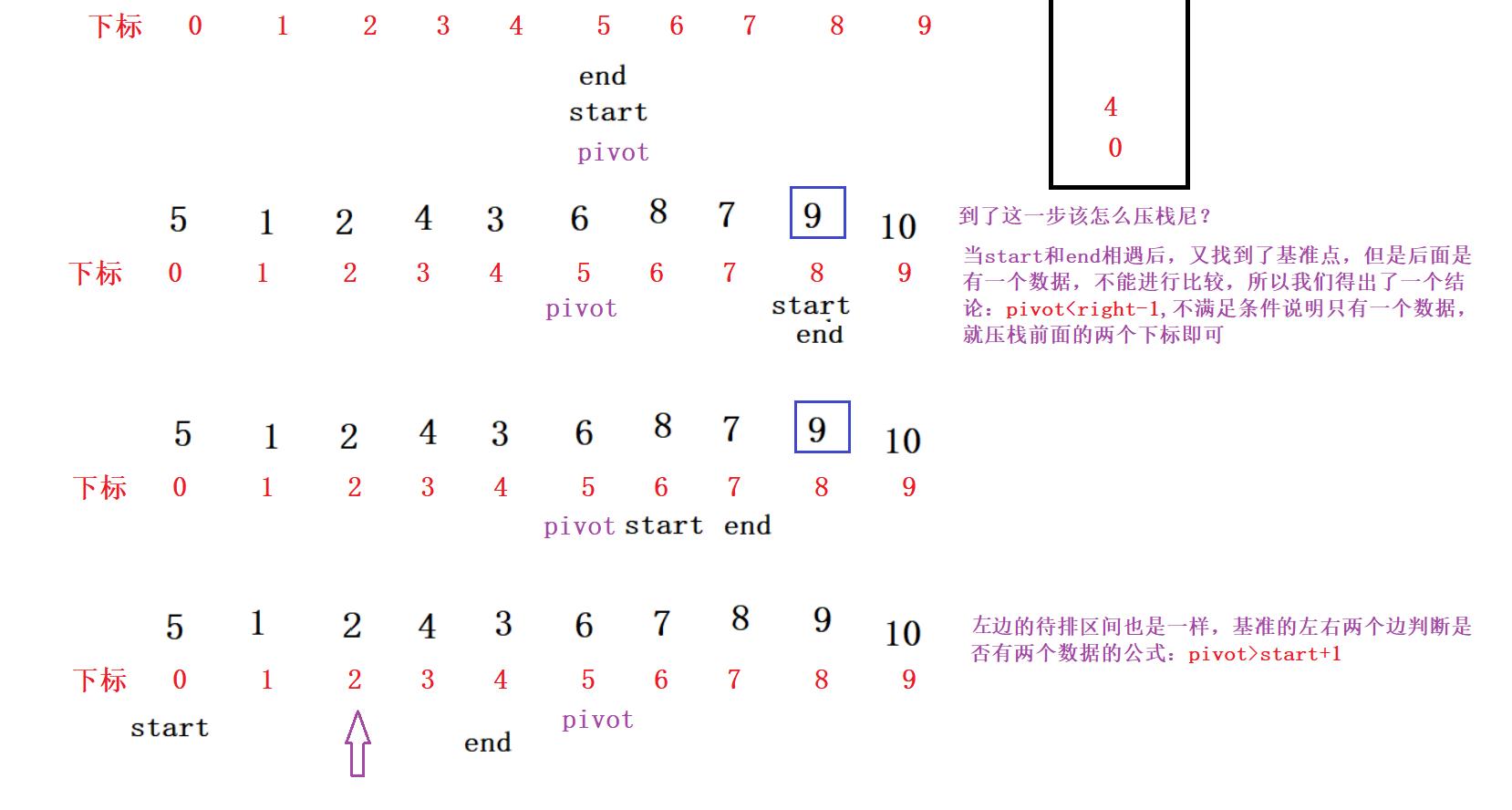
需邀注意的点：

压栈的基准点左右两点是否有两个以上数据，所判断的公式是：pivot<right-1,不满足条件说明只有一个数据，就压栈前面的两个下标即可。左边的待排区间也是一样，基准的左边判断是否有两个数据的公式是：pivot>start+1。

👨‍🦲👩‍🦲👩‍🔬代码：

public static void quickSort(int[] array) {
        Stack<Integer> stack = new Stack<>();
        int start = 0;
        int end = array.length-1;
        int pivot = partition(array,start,end);
        if(pivot > start+1) {//判断左边是否有两个数据
            stack.push(start);
            stack.push(pivot-1);
        }
        if(pivot < end-1) {//判断右边是否有两个数据
            stack.push(pivot+1);
            stack.push(end);
        }
        while (!stack.empty()) {
            end = stack.pop();
            start = stack.pop();
            pivot = partition(array,start,end);
            if(pivot > start+1) {
                stack.push(start);
                stack.push(pivot-1);
            }
            if(pivot < end-1) {
                stack.push(pivot+1);
                stack.push(end);
            }
        }
    }

以上就是快排最核心的点了，必须全掌握，若想看全代码可以 点击 Github ,

铁汁们，觉得笔者写的不错的可以点个赞哟❤🧡💛💚💙💜🤎🖤🤍💟，收藏关注呗，你们支持就是我写博客最大的动力

以上是关于深入了解快排 以及 优化的主要内容，如果未能解决你的问题，请参考以下文章

深入浅出：了解前后端分离优势前后端接口联调以及优化问题

三种快速排序以及快速排序的优化

快速排序（经典快排以及随机快排）

带你深入理解 归并排序

深入理解快速排序和 STL 的 sort 算法

排序算法：堆排，快排的实现（快排的三种实现方法以及快排的优化）