[海军国际项目办公室]门童
Posted StaroForgin
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[海军国际项目办公室]门童相关的知识,希望对你有一定的参考价值。
门童
题目概述




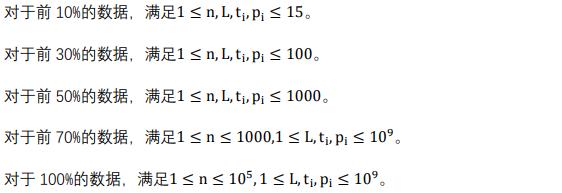
题解
妹妹最爱的树套树优化dp。
首先应该很容易 come up with 一种
d
p
dp
dp的思路。
由于牛牛整个过程中只有两个动作,待在门口,跑回去休息又跑回来。
我们可以定义
d
p
i
,
0
/
1
dp_{i,0/1}
dpi,0/1表示牛牛现在是待在门口还是再休息,但这样的话处理接待客人是很麻烦的,可能还要状压,我们不如就只看他待在门口接待客人的时候。
定义
d
p
i
dp_{i}
dpi表示他在时间
i
i
i时待在门口的总贡献,有两种转移,一种就是上一个时刻也待在门口,一种是从之前某个时刻跑回去休息,现在跑回来。
第一种的话客人一来就可以接待,直接加上客人的总价值就行了。
而第二种相当于在这段区间的客人来的时候,你是不会接待他们的,只有当你跑会来时才会接待他们,这就要算中间这段时间的贡献了。
我们同时发现,这样的转移第二种转移同时也是有区间的限制的,你不可能完全错过某个客人。
但我们发现如果像我们上面说的这样
d
p
dp
dp的话,我们发现真正有效的时间节点只有某个人到来的时间和某个人离开的时间。
因为我们的
d
p
dp
dp转移产生的贡献事实上都是斜率固定的直线的形式,所以加起来我们的最优决策点肯定时在某个时间节点上的。
我们可以只拿时间节点来作为
d
p
dp
dp状态,定义第
i
i
i个时间节点为
b
i
b_{i}
bi。
显然可以得到
d
p
dp
dp转移式,
d
p
i
=
max
(
d
p
i
−
1
−
(
b
i
−
b
i
−
1
)
x
0
,
0
+
∑
t
k
∈
(
b
i
−
1
,
b
i
]
f
k
p
k
,
max
j
=
L
i
R
i
(
d
p
j
−
L
(
x
1
,
0
+
x
0
,
1
+
2
x
1
,
1
)
+
(
b
i
−
b
j
−
2
L
)
x
1
,
1
+
∑
t
k
∈
(
b
i
−
1
,
b
i
]
f
k
(
t
k
+
p
k
−
b
i
)
)
)
dp_{i}=\\max\\left(dp_{i-1}-(b_{i}-b_{i-1})x_{0,0}+\\sum_{t_{k}\\in(b_{i-1},b_{i}]}f_{k}p_{k},\\max_{j=L_{i}}^{R_{i}}\\left(dp_{j}-L(x_{1,0}+x_{0,1}+2x_{1,1})+(b_{i}-b_{j}-2L)x_{1,1}+\\sum_{t_k\\in(b_{i-1},b_{i}]}f_k(t_k+p_k-b_i)\\right)\\right)
dpi=max⎝⎛dpi−1−(bi−bi−1)x0,0+tk∈(bi−1,bi]∑fkpk,j=LimaxRi⎝⎛dpj−L(x1,0+x0,1+2x1,1)+(bi−bj−2L)x1,1+tk∈(bi−1,bi]∑fk(tk+pk−bi)⎠⎞⎠⎞
对于
L
i
L_{i}
Li和
R
i
R_{i}
Ri,这两者显然是不降的,我们应该可以很容易地
O
(
n
)
O\\left(n\\right)
O(n)处理出来。
而对于上面的
d
p
dp
dp式子,我们是可以再化一下的,
d
p
i
=
max
(
d
p
i
−
1
−
(
b
i
−
b
i
−
1
)
x
0
,
0
+
∑
t
k
∈
(
b
i
−
1
,
b
i
]
f
k
p
k
,
b
i
x
1
,
1
−
L
(
x
1
,
0
+
x
0
,
1
+
2
x
1
,
1
)
+
max
j
=
L
i
R
i
(
d
p
j
−
b
j
x
1
,
1
+
∑
t
k
∈
(
b
i
−
1
,
b
i
]
f
k
(
t
k
+
p
k
−
b
i
)
)
)
dp_{i}=\\max\\left(dp_{i-1}-(b_{i}-b_{i-1})x_{0,0}+\\sum_{t_{k}\\in(b_{i-1},b_{i}]}f_{k}p_{k},b_{i}x_{1,1}-L(x_{1,0}+x_{0,1}+2x_{1,1})+\\max_{j=L_{i}}^{R_{i}}\\left(dp_{j}-b_{j}x_{1,1}+\\sum_{t_{k}\\in(b_{i-1},b_{i}]}f_{k}(t_{k}+p_{k}-b_{i})\\right)\\right)
dpi=max⎝⎛dpi−1−(bi−bi−1)x0,0+tk∈(bi−1,bi]∑fkpk,bix1,1−L(x1,0+x0,1+2x1,1)+j=LimaxRi