二叉搜索树与简单递归98108530701450669501538

Posted 2021-11-24 qq_40707462

98、验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

• 节点的左子树只包含小于当前节点的数。
• 节点的右子树只包含大于当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

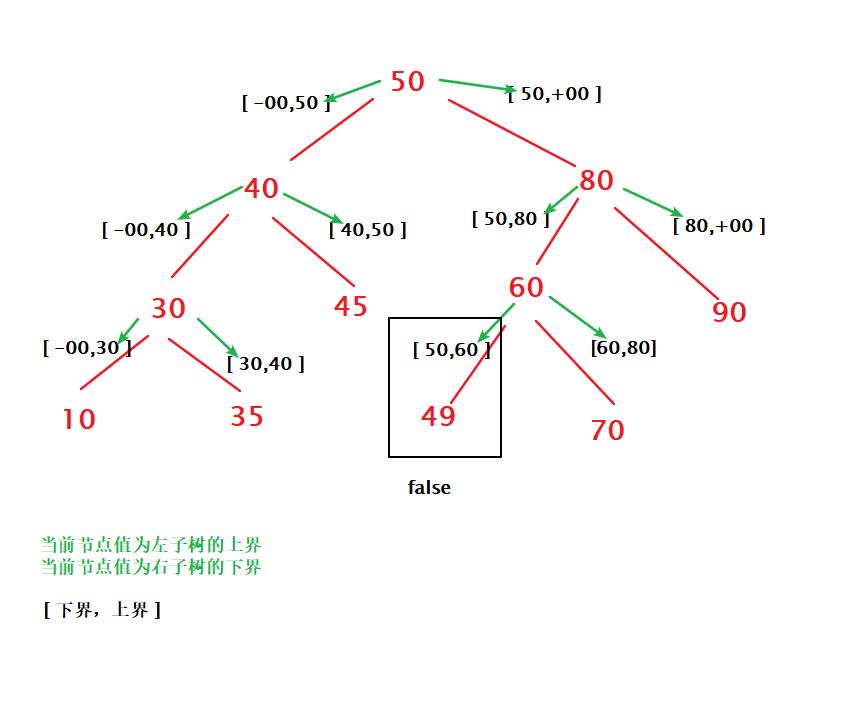
思路一：递归
不能单纯判断当前节点与左右的大小，比如

    5
 4     6
     3   7

这个3比4小，是不可以的。所以：

• 对于左节点，当前节点及之后节点的最大值是他的父节点；
• 对于右节点，当前节点及之后节点的最小值是他的父节点；

import math
class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        def dfs(root,maxval,minval):
            if not root:
                return True
            if root.val>=maxval or root.val<=minval:
                return False
            return dfs(root.left,root.val,minval) and dfs(root.right,maxval,root.val)
        
        return(dfs(root,math.inf,-math.inf))

class Solution {
    public boolean isValidBST(TreeNode root) {
        return dfs(root,Long.MIN_VALUE,Long.MAX_VALUE);
    }
    public boolean dfs(TreeNode root,long min,long max){
        if(root==null) return true;
        if(root.val>=max || root.val<=min) return false;
        return dfs(root.left,min,root.val) && dfs(root.right,root.val,max);
    }
}

思路二：中序遍历
若中序遍历的结果是严格递增的，则符合题意，用n记录前一个数的大小
中序遍历

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        stack=[]
        n=-math.inf

        while stack or root:
            if root:
                stack.append(root)
                root=root.left
            else:
                temp=stack.pop()
                if temp.val<=n:
                    return False
                n=temp.val
                root=temp.right
        return True

108、将有序数组转换为二叉搜索树

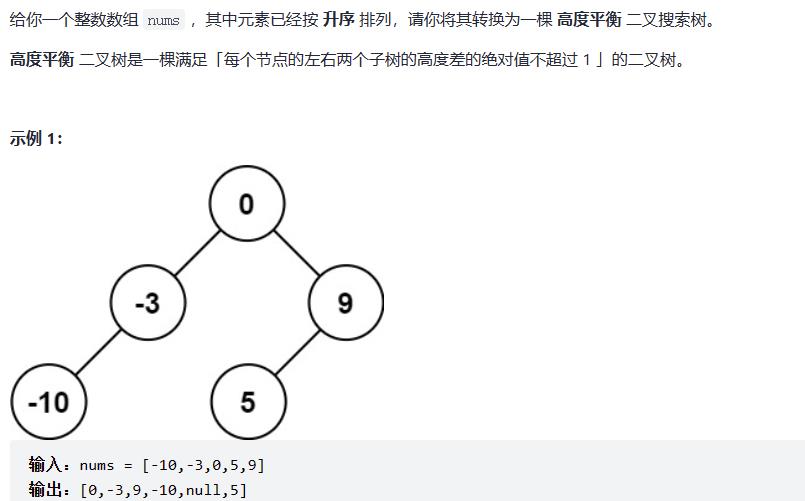
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        if(nums.length==0) return null;
        return dfs(nums,0,nums.length-1);
    }
    public TreeNode dfs(int[] nums,int left,int right){
        if(left>right) return null;
        int mid=(left+right)/2;
        TreeNode root=new TreeNode(nums[mid]);
        root.left=dfs(nums,left,mid-1);
        root.right=dfs(nums,mid+1,right);
        return root;
    }
}

530、二叉搜索树的最小绝对差

给你一棵所有节点为非负值的二叉搜索树，请你计算树中任意两节点的差的绝对值的最小值。

思路一：中序遍历存入列表，列表递增，相邻值之间差最小

class Solution {
    List<Integer>list=new ArrayList<>();
    public int getMinimumDifference(TreeNode root) {
        dfs(root);
        int res=Integer.MAX_VALUE;
        for(int i=1;i<list.size();i++){
            res=Math.min(res,list.get(i)-list.get(i-1));
        }
        return res;
    }
    public void dfs(TreeNode root){
        if(root==null) return;
        dfs(root.left);
        list.add(root.val);
        dfs(root.right);
    }
}

思路二：递归中序遍历
在递归中途更新最小值

class Solution {
    int res=Integer.MAX_VALUE;
    TreeNode pre;
    public int getMinimumDifference(TreeNode root) {
        dfs(root);
        return res;
    }
    public void dfs(TreeNode root){
        if(root==null) return;
        dfs(root.left);

        if(pre!=null) res=Math.min(res,root.val-pre.val);
        pre=root;

        dfs(root.right);
    }
}

701、二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点和要插入树中的值，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

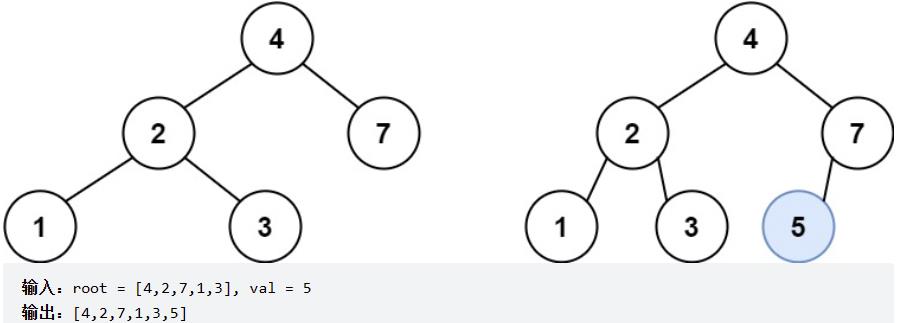
注意！！一定可以插在树的叶子上

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        //一定可以插在树的叶子上
        if(root==null){
            TreeNode node=new TreeNode(val);
            return node;
        }
        if(root.val>val) root.left=insertIntoBST(root.left,val);
        if(root.val<val) root.right=insertIntoBST(root.right,val);

        return root;
    }
}

450、删除二叉搜索树中的节点

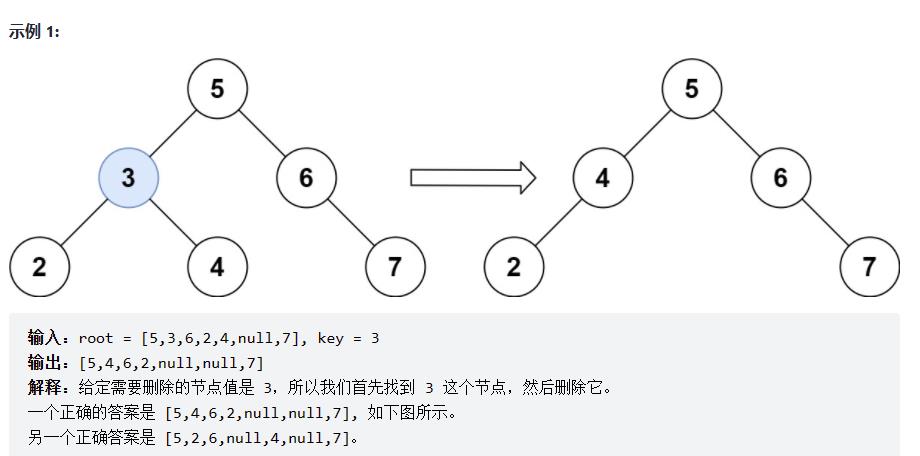
思路：

public TreeNode deleteNode(TreeNode root, int key) {
        if(root==null) return null;
        if(root.val==key){
			单层逻辑
        }
        if(root.val>key) root.left=deleteNode(root.left,key);
        if(root.val<key) root.right=deleteNode(root.right,key);
        return root;
    }

递三步：
①终止条件
②单层逻辑
③处理左右

每一层有以下五种情况：

• 第一种情况：没找到删除的节点，遍历到空节点直接返回了 找到删除的节点
• 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点
• 第三种情况：删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点
• 第四种情况：删除节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
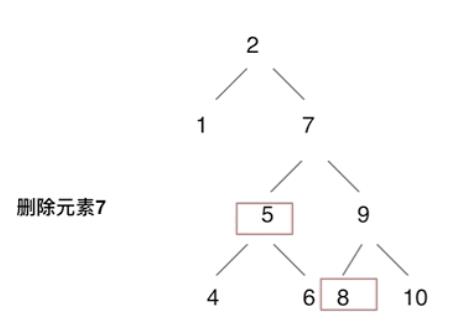
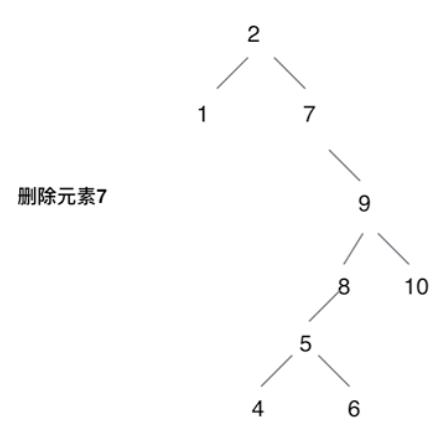
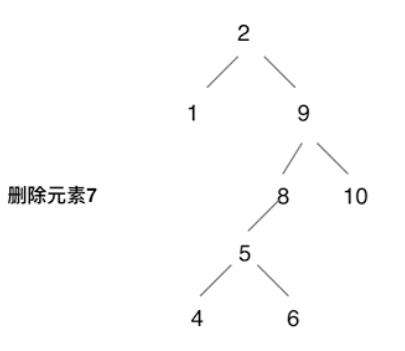
• 第五种情况：左右孩子节点都不为空，则将删除节点的左孩子，放到删除节点的右子树的 最左面节点 的左孩子上，返回删除节点右孩子为新的根节点。

eg 5放在8下，9接替7的位置

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if(root==null) return null;//一
        if(root.val==key){
            //二三四
            if(root.left==null) return root.right;
            else if(root.right==null) return root.left;
            //五，都不为空
            else{
                TreeNode node=root.right;//找到右子树最左边的节点
                while(node.left!=null) node=node.left;
                node.left=root.left;//root的左节点搬下来
                root=root.right;//替换root
                return root;
            }
        }
        if(root.val>key) root.left=deleteNode(root.left,key);
        if(root.val<key) root.right=deleteNode(root.right,key);
        return root;
    }
}

669、修剪二叉搜索树

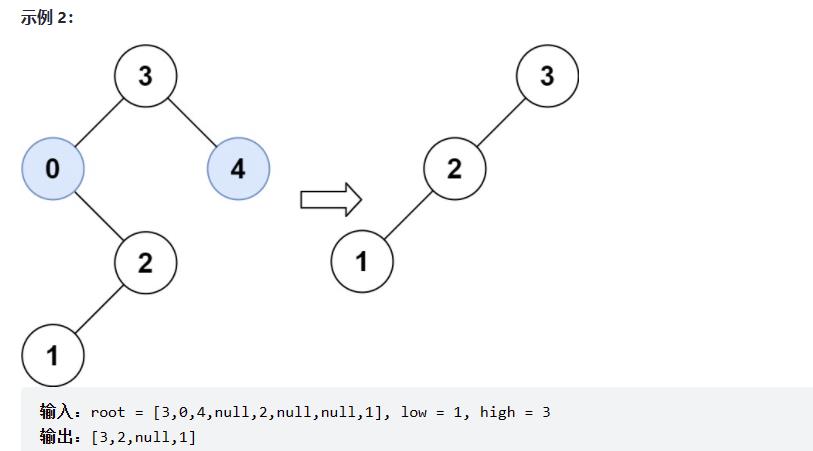
class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if(root==null) return null;
        if(root.val<low) {
            TreeNode rnode=trimBST(root.right,low,high);
            return rnode;
        }
        if(root.val>high){
            TreeNode lnode=trimBST(root.left,low,high);
            return lnode;
        }
        root.left=trimBST(root.left,low,high);
        root.right=trimBST(root.right,low,high);
        return root;
    }
}

501、二叉搜索树中的众数

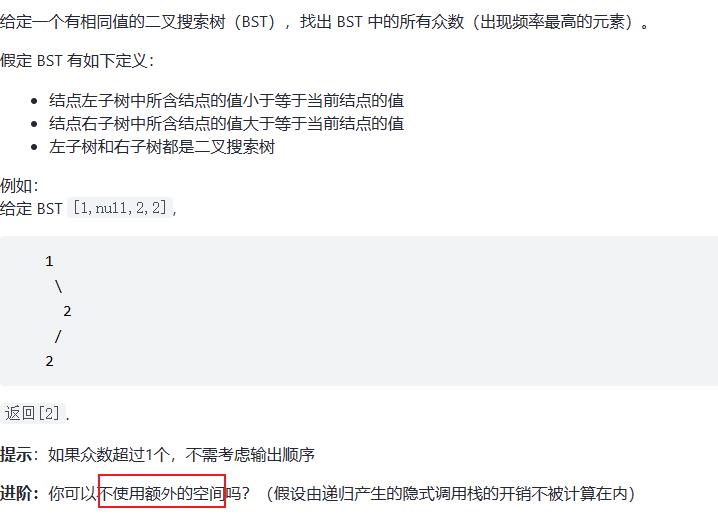
思路：
正常来说，中序遍历得到非递减数组，然后求数组众数即可，但消耗额外空间；

已知遍历顺序肯定是非递减，如果有相同的数肯定连在一起，可以在遍历途中维护一个表示当前数字出现几次的count，当前出现最对的次数maxCount，和记录前一个节点pre

• cur==pre; count++;
• 否则，清空count
• 如果count>maxCount，清空res，重新开始记录

class Solution {
    List<Integer>res=new ArrayList<>();
    TreeNode pre=null;
    int count=0;
    int maxCount=0;
    public int[] findMode(TreeNode root) {
        find(root);
        return res.stream().mapToInt(Integer::intValue).toArray();
    }
    public void find(TreeNode root){
        if(root==null) return;

        find(root.left);

        int cur=root.val;
        //计数
        if(pre==null || root.val!=pre.val) count=1;//重新开始计数
        else count++;
        //检查是否max
        if(count==maxCount){
            res.add(root.val);
        }else if(count>maxCount){
            res.clear();
            res.add(root.val);
            maxCount=count;
        }
        pre=root;

        find(root.right);
    }
}

538、把二叉搜索树转换为累加树

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

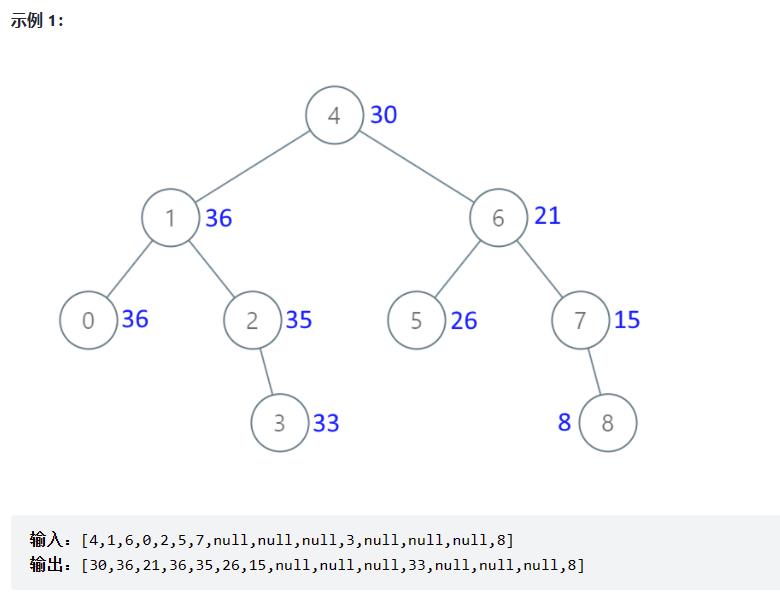
按【右中左】的顺序累加，就是一个有序数组[2, 5, 13]，求从后到前的累加数组，也就是[20, 18, 13]

class Solution {
    int pre=0;
    public TreeNode convertBST(TreeNode root) {
        if(root==null) return null;
        convertBST(root.right);

        root.val+=pre;
        pre=root.val;

        convertBST(root.left);
        return root;
    }
}