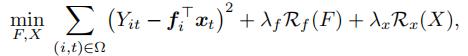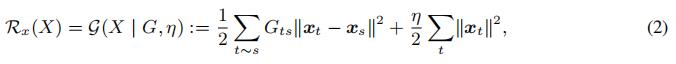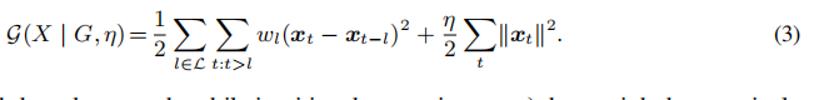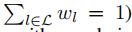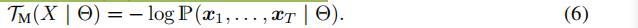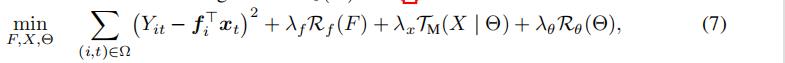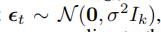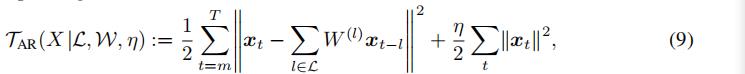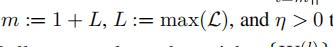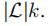论文笔记:Temporal Regularized Matrix Factorization forHigh-dimensional Time Series Prediction
Posted UQI-LIUWJ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了论文笔记:Temporal Regularized Matrix Factorization forHigh-dimensional Time Series Prediction相关的知识,希望对你有一定的参考价值。
0 摘要
时间序列预测问题在现代应用中变得越来越高维,如气候学和需求预测。例如,在需求预测中,项目数量可能高达50 000个。此外,数据通常是嘈杂的,充满缺失值。因此,现代应用程序需要高度可伸缩的方法,并且能够处理损坏或丢失值的噪声数据。然而,传统的时间序列方法往往无法解决这些问题。
在本文中,我们提出了一个时间正则化矩阵分解(TRMF)框架,支持数据驱动的时间学习和预测。我们开发了新的正则化方案,并使用了可扩展的矩阵分解方法,这非常适合具有许多缺失值的高维时间序列数据。
我们提出的TRMF是高度通用的,并包含了许多现有的时间序列分析方法。在学习自回归框架中的依赖性的背景下,我们对图正则化方法进行了有趣的连接。实验结果表明,TRMF在可扩展性和预测质量方面具有优越性。特别是,TRMF在处理50,000维度的问题时比其他方法快两个数量级,并且在真实世界的数据集(如沃尔玛电子商务数据集)上生成更好的预测。
1 introduction
传统的时间序列方法,比如自回归模型(autoregressive)和动态线性模型(DLM),主要关注于低维时序数据,无法解决我们之前说的高维数据和有缺失值的问题。
建模高维时间序列数据的一种自然方法是采用矩阵的形式,行对应于每个一维时间序列,列对应于时间点。鉴于n个时间序列之间通常是高度相关的,已经有人尝试应用低秩矩阵分解(MF)或矩阵补全(MC)技术来分析高维时间序列。与上面的AR和DLM模型不同,最先进的MF方法在n范围内线性扩展,因此可以处理大型数据集。
低秩矩阵分解的目标函数如下:
这里Ω是有数据的条目的集合。
,
是低秩特征矩阵F和X的正则项。这通常在避免过拟合和/或鼓励embedding中出现某些特定的时间结构特征方面发挥作用。
最普通的正则项是
(F是Forbenius范数) ,很显然它不太适用于时间序列问题,因为它没有考虑时间嵌入{xt}的顺序。
线性代数笔记:Frobenius 范数_UQI-LIUWJ的博客-CSDN博客
大多数现有的MF方法采用基于图的方法来处理时间依赖性。具体来说,依赖关系由加权相似图描述,并通过拉普拉斯正则项进行约束。
【这里的图是同一个特征的时序关系拼接成图,也就是X矩阵的一行】
然而,这种基于图的正则化在两个时间点之间存在负相关(负边图)的情况下失效。
有负权重边的图可以有拉普拉斯矩阵吗?_UQI-LIUWJ的博客-CSDN博客
与其他数据中有显式图信息的场景(如社交网络图)不同,在我们的问题下,显式时间依赖结构通常是没有的,必须推断或近似。
此外,现有的MF方法虽然对过去点的缺失值产生了良好的估计,但在预测未来值方面却很差,这是时间序列分析中感兴趣的问题。
在本文中,我们提出了一个新的时间正则化矩阵分解框架(TRMF)用于高维时间序列分析。
在TRMF中,我们考虑了一种原则性的方法来描述潜在时间嵌入之间的时间依赖性结构{xt},并设计了一个时间正则化器来将这种时间依赖性结构纳入标准MF公式。
与大多数现有的MF方法不同,我们的TRMF方法支持数据驱动的时间依赖性学习,并为矩阵分解方法带来预测未来值的能力。此外,TRMF方法继承了MF方法的属性,即使在存在许多缺失值的情况下,TRMF也可以轻松处理高维时间序列数据。
作为一个具体的例子,我们展示了一种新的自回归时间正则化器,它鼓励时间嵌入{xt}之间的AR(autoregressive)结构。
我们还将提出的正则化框架与基于图的方法[18]联系起来,其中甚至可以解释负相关。
这种连接不仅有助于更好地理解我们的框架所包含的依赖结构,而且还有助于使用现成的高效求解器(如GRALS[15])直接求解TRMF。
2 具有时间依赖性的数据的现有矩阵分解方法
标准MF公式对列的排列保持不变(个人理解是列不管怎么变,权重矩阵保持不变),这不适用于具有时间依赖性的数据。
因此,对于时间依赖性{xt},大多数现有的时间MF方法都转向基于图的正则化框架[18],并用图编码时间依赖性。
2.1 时间依赖性的图正则化
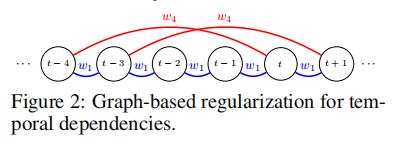
令G是一个时间依赖性{xt}的图,Gts是第t个点和第s个点之间的边权重。一种常见的正则化方式如下公式:
其中t~s代表了第t个点和第s个点之间的边;第二个正则化项是用来保证强凸性
一个很大的Gts可以保证xt和xs在欧几里得距离上很接近
为了保证
的凸性,我们让Gts≥0
为了将基于图的正则化应用于时间依赖关系上,我们需要通过滞后集L和权值向量w重复地指定各个点之间的依赖模式,以便距离L的所有边t ~ s共享相同的权值
于是上面的公式2可以改写成:
这种直接使用基于图的方法虽然很直观,但有两个问题:
a)两个时间点之间可能存在负相关依赖关系;
b)显式的时态依赖结构通常不可用,必须使用者进行推断。
于是,很多现有的这种正则化的模型只能考虑很简单的时间依赖关系(比如滞后集L很小,L={1}),和/或 统一的权重(比如不管两个点之间距离是多少,权重统一设置为1)
这导致现有MF方法对大规模时间序列的预测能力较差。
2.2 学习时间依赖性的挑战
也许有人会想:那我权重参数w让机器自己学不就好了吗?
· 在这种假设下,我们有了以下的优化方程:
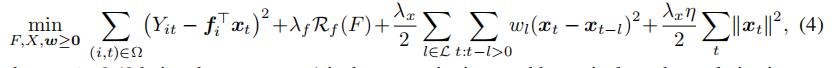
我们不难发现,最终的优化结果,是所有的w都是0,意为没有空间依赖关系的时候,目标函数达到最小值。
为了避免让所有的w都是0,有人想到可以给w的和加上一个限制,比如
同样地,我们不难发现,最终的优化结果是
对应的wl*是1,其他的w是0
因此,通过简单地在MF公式中插入正则化器来自动学习权重并不是一个可行的选择。
3 TRMF temporal regularized matrix factorization
为了解决2.1和2.2节中提到的限制,我们提出了时间正则化矩阵分解(TRMF)框架,这是一种将时间依赖性纳入矩阵分解模型的新方法。
与前面提到的基于图的方法不同,我们建议使用经过充分研究的时间序列模型来明确地描述{xt}之间的时间依赖性。
是一个高斯噪声向量
是一个时间序列模型,参数是Θ和滞后集L
L是一个包含滞后指标L的集合,表示t和t-l时间点之间的相关性
Θ捕捉时间相关性的权重信息(如AR模型中的转移矩阵)。
基于此,我们提出了一个新的正则化项
,这可以鼓励模型依照时间序列
我们令
当θ给定的时候,我们令
为矩阵分解的一个正则化项;当θ未知的时候,我们令θ为另外一部分参数,并且设计Rθ以作为另一个正则化项。
通过交替地优化更新F,X,Θ,可以解决上面的优化方程。
3.1 TRMF中数据驱动的时间依赖性学习
在2.2中,我们展示了直接使用基于图的正则化项来合并时间依赖性会导致权重的平凡解(全0解)。
在TRMF中,当F和X是固定的时候,式(7)可以简化为:
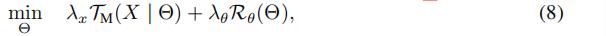
其中第一项可以看成:min -logP(x1,....xT|θ),即max P(x1,....xT|θ)
也就是说,后一项可以看成最大后验概率
3.2 TRMF时间序列分析
我们可以看到,TRMF可以无缝地处理在分析具有时间依赖性的数据时经常遇到的各种任务:
3.2.1 时间序列预测
一旦我们有了潜在的嵌入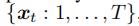 的
的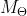 ,我们可以预测未来的嵌入
,我们可以预测未来的嵌入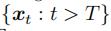 ,然后使用来预测结果
,然后使用来预测结果
3.2.2 缺失值补全

4 一种新的自回归时间正则化算法
在小节3中,我们大致介绍了TRMF的框架:正则项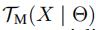 (有时间序列模型
(有时间序列模型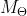 确定)
确定)
在这一小节中,我们将介绍一种TRMF框架:自回归模型,参数为滞后集L和权重
我们令xt是以下形式

是一个高斯噪声向量
于是,时间正则化项
可以写成:
其中
由于每个
所以我们有
个参数要学习,这可能导致过拟合
为了避免过拟合,同时为了生成更可解释的结果,我们人为定义
为对角矩阵,这可以使得参数量减少至
出于简化的考虑,我们使用W来表示这个k×L的矩阵,其中第l列表示
的对角线元素
. 简化后,我们有:
xt表示时刻t的向量
将式(10)代入式(7),有式(12):
我们将式(12)命名为TRMF-AR
4.1 不同时间序列之间的关联性
尽管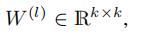 是对角阵,但是TRMF还是可以建模不同时间序列(X矩阵不同行之间)的关联性。这个关联性在特征矩阵F中体现
是对角阵,但是TRMF还是可以建模不同时间序列(X矩阵不同行之间)的关联性。这个关联性在特征矩阵F中体现
4.2 滞后集L的选择
TRMF中L的选择更加灵活。因此,TRMF可以提供重要的优势:
首先,因为不需要指定权重参数W,可以选择更大的L来考虑长期依赖性,这也可以产生更准确和稳健的预测。
其次,L中的时延不需要是连续的,这样就可以很容易地嵌入关于周期性或季节性的领域知识。例如,对于具有一年季节性的每周数据,可以考虑L ={1, 2, 3, 51, 52, 53}。
4.3 参数的优化
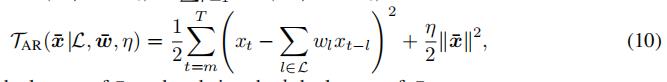
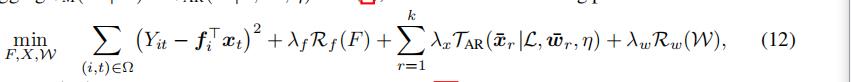
5 实验
5.1 数据集
对于synthetic数据集,我们先随机生成一个
,,生成{xt},它满足AR过程,且滞后集L={1,8}。然后Y通过
生成
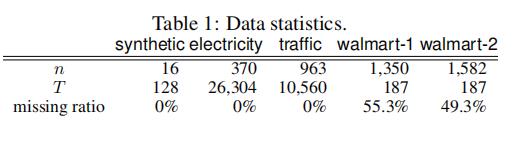
电力和交通数据集从UCI存储库获得,而Walmart -1和Walmart -2是来自Walmart电子商务的两个专有数据集,其中包含每周的销售信息。由于缺货等原因,missing rate分别为55.3%和49.3%。为了评价预测性能,我们考虑了归一化偏差(ND)和归一化均方根(NRMSE)。
5 .2 实验结果
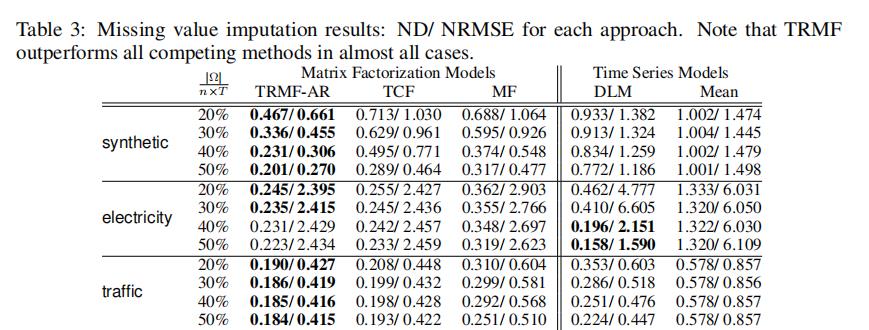
以上是关于论文笔记:Temporal Regularized Matrix Factorization forHigh-dimensional Time Series Prediction的主要内容,如果未能解决你的问题,请参考以下文章