强化学习笔记：Q-learning

Posted 2021-11-24 UQI-LIUWJ

        在强化学习笔记： MDP - Policy iteration_UQI-LIUWJ的博客-CSDN博客 中我们提到了Q-table，同时我们说到，对于model-free的MDP，最开始这张 Q 表格会全部初始化为零，然后 agent 会不断地去和环境交互得到不同的轨迹。 当交互的次数足够多的时候，我们就可以估算出每一个状态下，每个行动的平均总收益，然后去更新这个 Q 表格。

        在没法获取 MDP 的模型情况下，我们可以通过以下两种方法来估计某个给定策略的价值：

• Monte Carlo policy evaluation
• Temporal Difference(TD) learning

这里我们介绍蒙特卡洛策略估计

1 Monte Carlo policy evaluation

        蒙特卡罗(Monte-Carlo，MC)方法是基于采样的方法，我们让 agent 跟环境进行交互，就会得到很多轨迹。每个轨迹都有对应的 return：

        

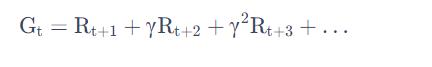
         我们把每个轨迹的 return 进行平均，就可以知道某一个策略下面对应状态的价值

         MC 是用 经验平均回报(empirical mean return) 的方法来估计。

        MC 方法的优点：不需要 MDP 的转移函数和奖励函数

        MC 方法的局限性：只能用在有终止的 MDP 。

1.1 MC算法

        为了得到评估 v(s)，我们进行了如下的步骤：
1）在每个回合中，如果在时间步 t 状态 s 被访问了，那么

        1.1）状态 s 的访问数 N(s) 增加 1

        1.2）状态 s 的总的回报S(s) 增加Gt​。

2）状态 s 的价值可以通过 return 的平均来估计，即 v(s)=S(s)/N(s)。

3）根据大数定律，只要我们得到足够多的轨迹，就可以趋近这个策略对应的价值函数。 （大数定律：如果统计数据足够大,那么事物出现的频率就能无限接近它的期望值。）

1.1.1 增量均值 

        假设现在有样本x1​,x2​,⋯，我们可以把经验均值(empirical mean)转换成 增量均值(incremental mean) 的形式，如下式所示：

        

         通过这种转换，我们就可以把上一时刻的平均值跟现在时刻的平均值建立联系，即：

                

         其中

        

        当我们得到 xt​，就可以用上一时刻的值来更新现在的值。

 1.2  incremental MC

我们采集数据，得到一个新的轨迹

 

对于这个轨迹，我们采用增量的方法进行更新，如下式所示：

 

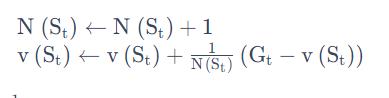
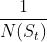我们可以想成学习率

1.3 MC和Policy evaluation 的异同 

强化学习笔记：马尔可夫决策过程 Markov Decision Process(MDP)_UQI-LIUWJ的博客-CSDN博客

        Policy evaluation（有的地方叫动态规划，DP）也是常用的估计价值函数的方法。在动态规划里面，我们使用了 bootstrapping 的思想。bootstrapping 的意思就是我们基于之前估计的量来估计一个量。

           Policy evaluation就是用 Bellman expectation backup，通过上一时刻的值来更新当前时刻这个值，不停迭代，最后可以收敛

 

         MC 是通过 empirical mean return （实际得到的收益）来更新它，对应树上面蓝色的轨迹，我们得到是一个实际的轨迹，实际的轨迹上的状态已经是决定的，采取的行为都是决定的。

        MC 得到的是一条轨迹，这条轨迹表现出来就是这个蓝色的从起始到最后终止状态的轨迹。现在只是更新这个轨迹上的所有状态，跟这个轨迹没有关系的状态都没有更新。

 1.3.1 MC相比于DP的优点

• MC 可以在不知道环境具体情况（奖励函数、状态转移概率）的情况下 work，而 DP 是 model-based。
• MC 只需要更新一条轨迹的状态，而 DP 则是需要更新所有的状态。状态数量很多的时候（比如一百万个，两百万个），DP 这样去迭代的话，速度是非常慢的。这也是 sample-based 的方法 MC 相对于 DP 的优势。