Leetcode打卡——二叉树的4种遍历你真的会了吗（Leetcode官解迭代法解法解析）

Posted 2021-11-23 被折叠的小饼干

哈喽大家，这里是小饼干，面向就业编程，持续更新学习路径，欢迎关注点赞鸭

这周开始刷二叉树了，一上来就是4种二叉树遍历，发现之前自己会了但没有完全会= =，

二叉树的遍历可以分为：

（一）二叉树的深度优先遍历：
①前序遍历
②中序遍历
③后序遍历

（二）二叉树的广度优先遍历：
层序遍历

递归写法看不懂的可以先看看这个：
Leetcode代码随想录题解
代码随想录

递归写法都挺简单，算是easy题，迭代就好难QAQ,medium或者hard,写法还五花八门的。
有人说会了递归法就行了，能写出来就行，如果不懂迭代法，你真的懂了递归的过程了嘛？迭代就是对递归细节化的拆分。
还有见迭代法写的完全没迭代的味儿，遍历”的本质是对内存的有序访问，失去了访问顺序，即便用各种数据结构恢复了这个次序，遍历本身也显得毫无意义,有人把前序遍历左右入栈顺序改了，最后结果reverse一下就成后序遍历了，虽然结果对了，但还是感觉很别扭。这篇主要讲讲怎么用迭代法进行遍历。
只有当各个节点以“左->右->中”的次序依次出现在迭代的loop当中时，它才是真正的后序遍历，Leetcode官解就很可，咱就直接拿官解写法讲了。

前中后序遍历的本质还是深度优先遍历，所以要用到栈，用来保存当前走过的节点的路径，其后进先出的特性可以帮助我们遍历完当前节点及其子节点后返回上一节点。

具体的解释都写在代码里了。

1.Leectcode144. 二叉树的前序遍历

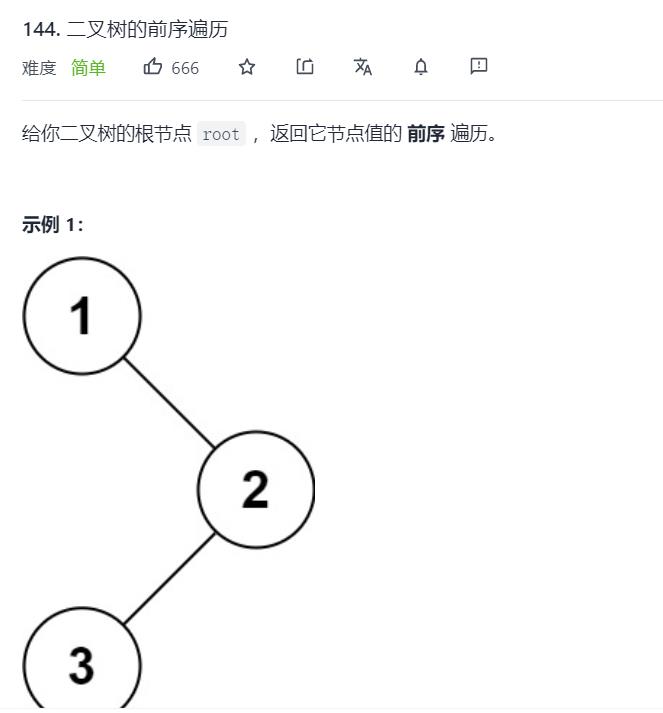
法一：递归

class Solution {
public:
    vector<int>ans;
    vector<int> preorderTraversal(TreeNode* root) {    
        preorder(root);
        return ans;
    }
    void preorder(TreeNode *root){
        if(root==NULL)return ;
        ans.push_back(root->val);
        preorder(root->left);
        preorder(root->right);
    }
};

法二：迭代

class Solution {
public:
    
    vector<int> preorderTraversal(TreeNode* root) {  
       vector<int>ans;  
       stack<TreeNode*>st;
       //用来表示当前遍历到的节点
       TreeNode *node=root;
       
//为什么循环会有两个条件呢？不着急，我们先往下看
       while(!st.empty()||node){
       //前序遍历顺序为中左右，即根结点->根结点的左子树的根结点->根结点的左子树的的根结点的左子树的根结点->...开始套娃->根结点的右子树的根结点
       //所以我们先一直向左走，并记录路径上的节点，先中间节点所以可以把当前子树的根结点的值加到ans了
           while(node){
               st.push(node);
               ans.push_back(node->val);
               node=node->left;
           }
           //当node=NULL时，此时找到最左的叶节点，即最左子树的左孩子节点
           //左边遍历完了，我们就可以回到上一层，找到最左子树的根结点，根节点其实已经遍历过了，我们这里只是想退回一步
           node=st.top();
           //就差最左子树的右孩子节点了，右孩子节点为NULL就直接到上一层了，不为空就接着遍历一下，所以栈最左子树的根结点可以弹出了
           st.pop();
           //遍历最左子树的右节点
           node=node->right;
           //右节点为NULL就直接到上一层了，node=st.top(),不为空就接着遍历右子树，找到最左，就像对根结点开始的操作一样，但其实我们对左子树的操作也是这样，只是因为第一步是向左走的，所以不容易发现QVQ
       }
//又回到一开始的问题，为什么循环会有两个条件呢？
//（一）!st.empty()这个很好理解，就是栈里还有保存的上一层的根节点，所以要回接着遍历它们的右子树，是向上的
//（二）node!=NULL 说明当前node非空，需要对当前节点做下一步操作，是向下的

       return ans;
    }
    
    
};

现在大家可以自己试着理解下中序和后序代码了

2. Leectcode94. 二叉树的中序遍历

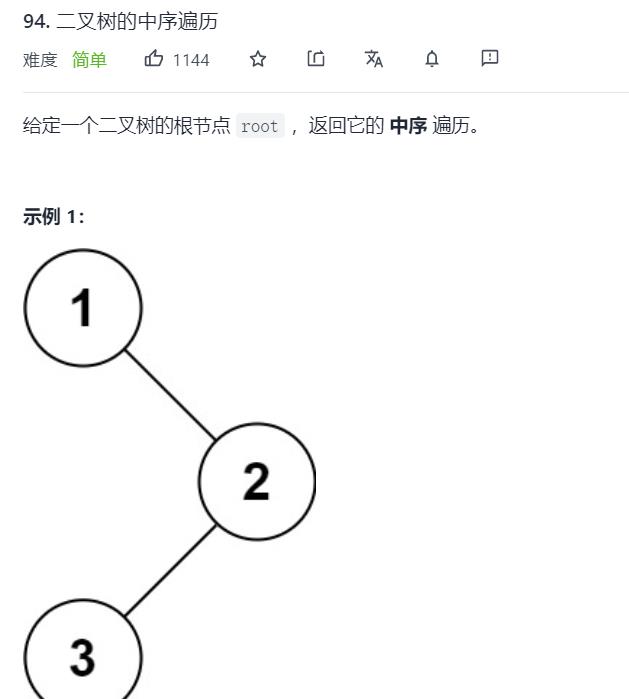
法一：递归

class Solution {
public:
    vector<int>ans;
    vector<int> inorderTraversal(TreeNode* root) {
         inorder(root);
         return ans;
    }
    void inorder(TreeNode *root){
        if(root==NULL)return;
        inorder(root->left);
        ans.push_back(root->val);
        inorderTraversal(root->right);

    }
};

法二：迭代

class Solution {
public:
    
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int>ans;
        stack<TreeNode *>st;
        TreeNode *node=root;
        while(!st.empty()||node){
            while(node){
                st.push(node);
                //这里中序遍历先左后中，所以ans没有记录中间节点的值
                node=node->left;
            }
            node=st.top(); 
            st.pop();
            ans.push_back(node->val);     
            node=node->right;
        }
        return ans;
    }
    
};

3.Leectcode145. 二叉树的后序遍历

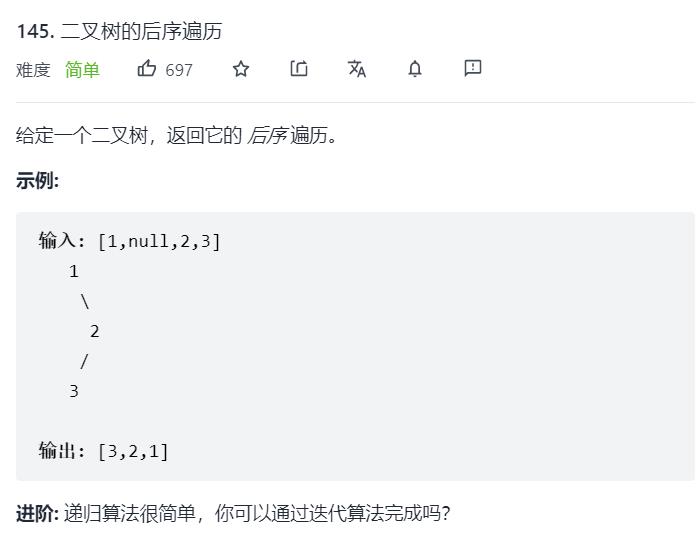
法一：递归

class Solution {
public:
    vector<int>ans;
    vector<int> postorderTraversal(TreeNode* root) {
         postorder(root);
         return ans;
    }
    void postorder(TreeNode *root){
        if(root==NULL)return;
        postorder(root->left);
        postorder(root->right);
        ans.push_back(root->val);
    }
};

法二：迭代

class Solution {
public:
    vector<int> postorderTraversal(TreeNode *root) {
        vector<int> res;
        if (root == nullptr) {
            return res;
        }

        stack<TreeNode *> stk;
        TreeNode *node=root;
        TreeNode *prev = nullptr;
        while (node != nullptr || !stk.empty()) {
            while (node != nullptr) {
                stk.push(node);
                node = node->left;
            }
            //左孩子结点为空，回到父结点
            node = stk.top();
            stk.pop();
            //很多人可能会问，这里怎么变了？pre又是什么？
            //这里其实跟之前是一样的，root->right == prev，说明右孩子节点已经遍历过了，这回是最后遍历中间节点，所以要先遍历完右子树
            //右孩子为空/右子树遍历过了，ans就可以加入根结点值了
            if (node->right == nullptr || node->right == prev) {
                res.push_back(node->val);
                prev = node;
                node = nullptr;
            } else {
                stk.push(node);
                node = node->right;
            }
        }
        return res;
    }
};

下面看看层序遍历，层序遍历的本质还是广度优先遍历，所以要用到队列，用来保存当前走过的节点的路径，其先进先出的特性可以帮助我们遍历完当前层节点再继续按顺序按顺序遍历下一层子节点。

4.Leetcode102.二叉树的层序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) { 
          vector<vector<int>>ans;
          if(root==NULL)return ans;
          queue<TreeNode*>q;
          q.push(root);
          while(!q.empty()){
              //当前队列元素个数恰好等于当前层元素个数
              int len=q.size();
              vector<int>level;
              for(int i=0;i<len;i++){
                  auto t=q.front(); 
                  q.pop();
                  level.push_back(t->val);
                  if(t->left)q.push(t->left);
                  if(t->right)q.push(t->right);
              }
              ans.push_back(level);
              
          }
          return ans;
    }
};

还没有看懂的小伙伴可能是还不太理解遍历过程，可以先看看官解的动态图，再回来看代码，最后记得自己多写几遍哈