堆的基本知识

Posted 2021-11-23 鸢也

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了堆的基本知识相关的知识，希望对你有一定的参考价值。

优先级队列（堆）

文章目录

优先级队列（堆）

前言

1、掌握堆的概念和实现

2、掌握PriorityQueue的使用

一、概念

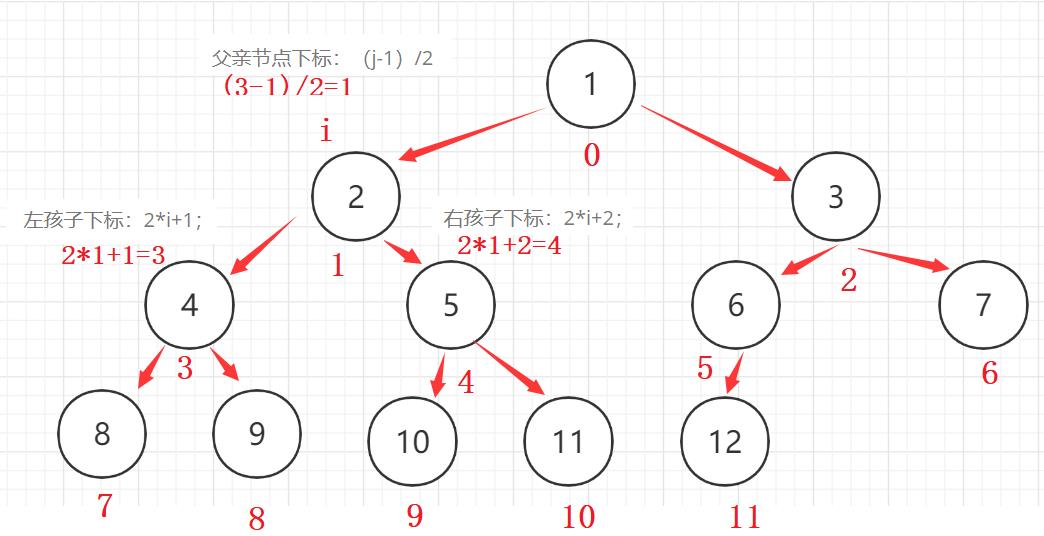
堆逻辑上是一课完全二叉树，是用二叉树的层序遍历方式放入数组中，也就是说是用顺序数组来存储，这样可以节省空间。

重要公式：

1、已知父亲节点小标是i

左孩子下标：2*i+1；

右孩子下标：2*i+2；

2、已知孩子节点是j

求父亲节点的下标：

父亲节点下标：（j-1）/2

1.1 堆的分类

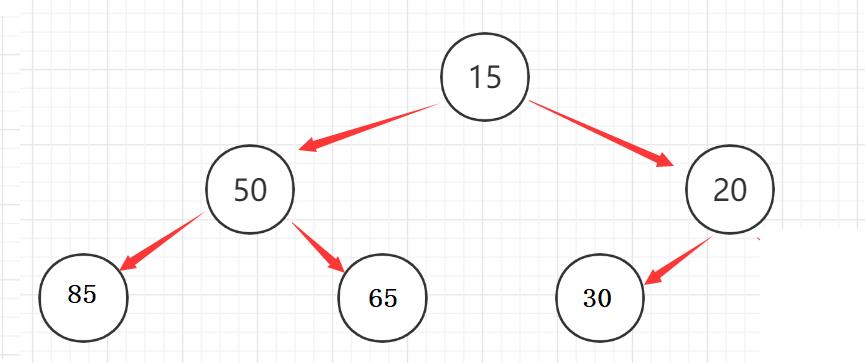
小堆：（小根堆，最小堆）父亲节点小于左右孩子节点，注意的是左右孩子没有大小关系；

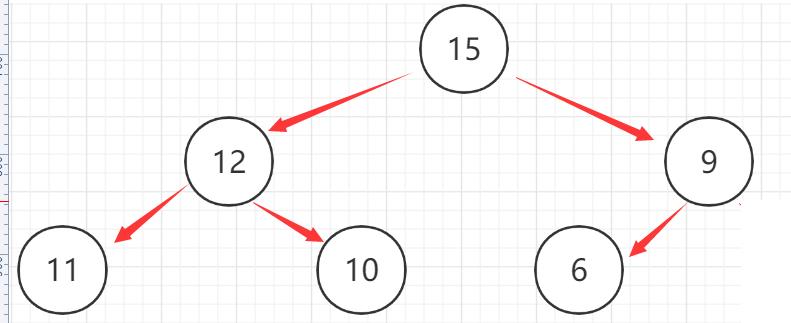
大堆：（大根堆，最大堆）父亲节点大于左右孩子节点，注意的是左右孩子没有大小关系；

1.2向下调整

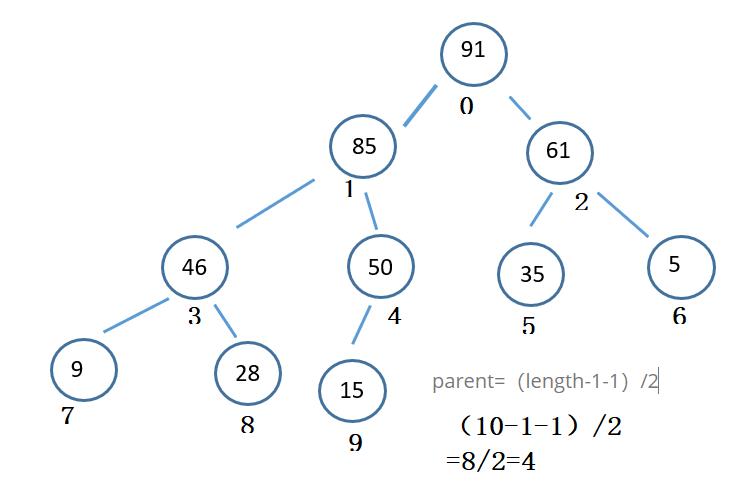
以向下调整实现堆的过程，以大根堆为例：

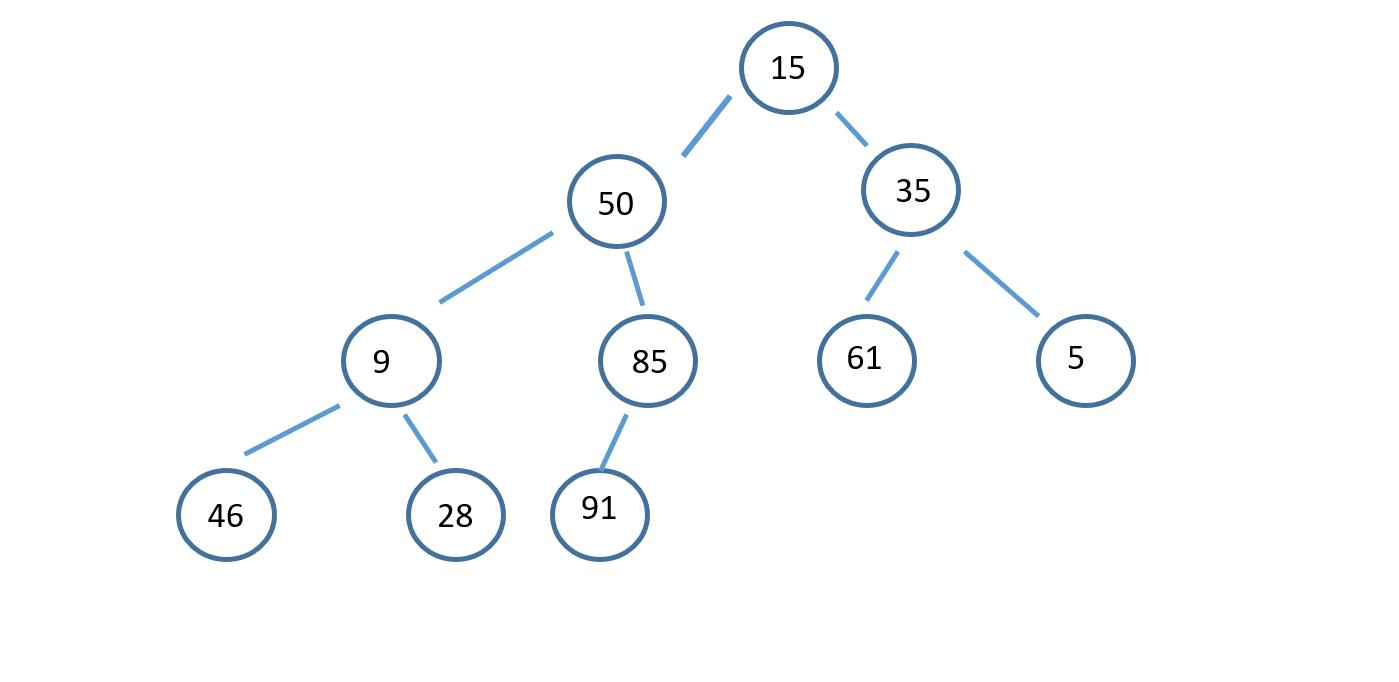
这里只演示了一半，完整版文件太大传不了😂😂😂😂，知道思想差不多也可以推了

向下调整，是每颗子树向下调整：

1、最开始调整的时候，是从最后一个子树开始调整；

2、有个很重要的公式是：找到最后一个子树的根节点

parent=（length-1-1）/2

向下调整代码如下：

 //大根堆是向下调整
    public void shiftDown(int parent) {
        int chlid=2*parent+1;//之前推了孩子公式

        //会有循环，条件是child小于数组才能操作
        while(chlid<this.usedSize) {
            //判断有没有右孩子，然后比较左右孩子的大小
            if(chlid+1<this.usedSize && this.elem[chlid]<this.elem[chlid+1]) {
                chlid++;
            }
            //走到这，子数已经是最大值，剩下的就是交换
            if(this.elem[chlid]>this.elem[parent]) {
                int tmp=this.elem[parent];
                this.elem[parent]=this.elem[chlid];
                this.elem[chlid]=tmp;
                parent=chlid;
                chlid=2*parent+1;
            } else {
                break;
            }
        }
    }

时间复杂度：一般都是最坏的情况，是从根一路遍历底层，所以就是完全二叉树的高度O（log(n)）

1.3 建堆

完整代码(大根堆）：

public class TestHeap {
    public int[] elem;
    public int usedSize;

    public TestHeap() {
        this.elem=new int[10];

    }
    public void creatBigHeap(int[] array) {
        for(int i=0;i<array.length;i++) {
            this.elem[i]=array[i];
            this.usedSize++;
        }

        for(int i=(this.usedSize-1-1)/2;i>=0;i--) {
            shiftDown(i);
        }
    }
    //大根堆是向下调整
    public void shiftDown(int parent) {
        int chlid=2*parent+1;

        //会有循环，条件是child小于数组才能操作
        while(chlid<this.usedSize) {
            //判断有没有右孩子，比较左右孩子的大小
            if(chlid+1<this.usedSize && this.elem[chlid]<this.elem[chlid+1]) {
                chlid++;
            }
            //走到这，子数已经是最大值，剩下的就是交换
            //这是大根堆，小根堆大于小于号改变一下就行了
            if(this.elem[chlid]>this.elem[parent]) {
                int tmp=this.elem[parent];
                this.elem[parent]=this.elem[chlid];
                this.elem[chlid]=tmp;
                parent=chlid;
                chlid=2*parent+1;
            } else {
                break;
            }
        }
}

时间复杂度：向下调整+循环：O(n * log(n))

实际上是O（n）

想了解可以看这个链接：堆排序中建堆过程时间复杂度O(n)怎么来的？

二、入队列

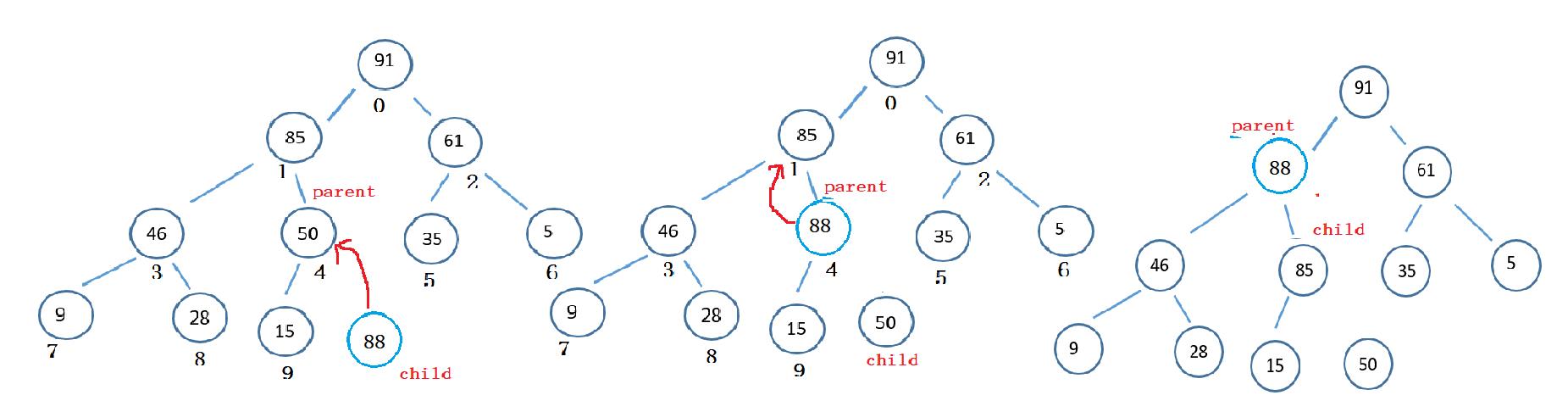
思路：把入队列的元素，放到数组的最后一个位置,保证这个堆是大根堆或者是小根堆，先判断顺序数组满不满,满就扩容,然后实现向上调整

2.1 向上调整

思路:定义孩子节点,和父亲节点,新的元素与父亲节点比较,大就交换,然后更新child,使child=parent

代码:

 public void shiftUp(int child) {
        int parent = (child-1)/2;
        while (parent >= 0) {
            if(this.elem[child] > this.elem[parent]) {
                int tmp = this.elem[child];
                this.elem[child] = this.elem[parent];
                this.elem[parent] = tmp;
                child = parent;
                parent = (child-1)/2;
            }else {
                break;
            }
        }
    }

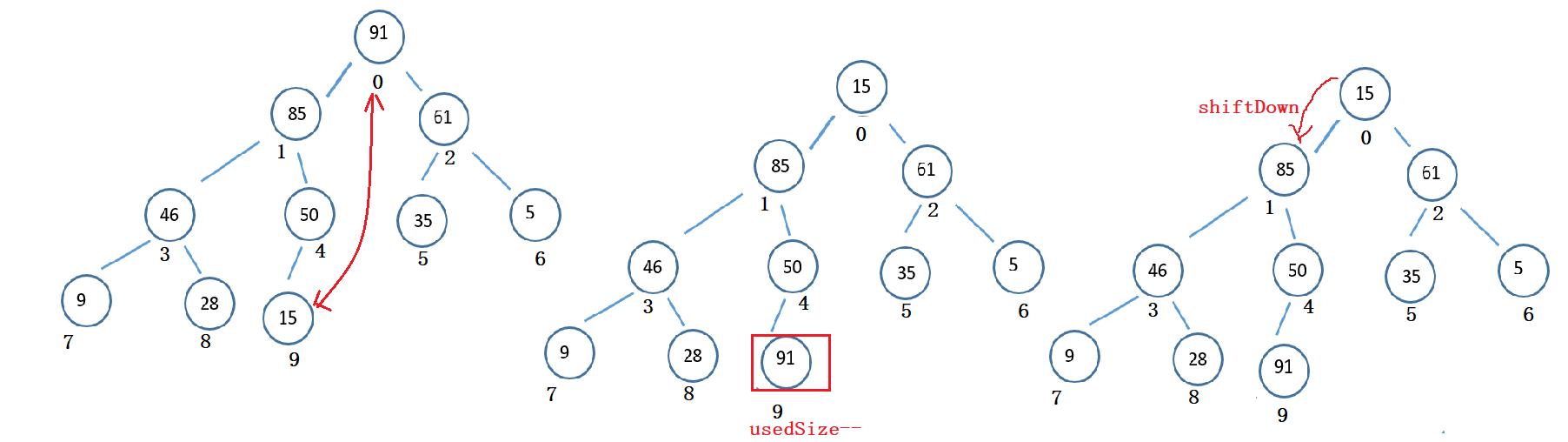
三、出队列

思路：因为是优先级队列，所以是出堆顶元素，用堆顶元素跟数组最后一个元素交换，再usedSize–，此时虽然交换完，但是他不是大根堆或者小根堆，所以用向下调整0下标这课树，来保证最后是大根堆。

代码：

 public int poll() {
        if(isEmpty()) {//队列为空抛出异常
            throw new RuntimeException("队列为空！");
        }
     //交换
        int tmp = this.elem[0];
        this.elem[0] = this.elem[this.usedSize-1];
        this.elem[this.usedSize-1] = tmp;
        this.usedSize--;
     //向下调整
        shiftDown(0);
        return tmp;
    }