CSI笔记:基于MUSIC Algorithm的DoA/AoA估计以及MATLAB实现
Posted Jiajia Shi
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了CSI笔记:基于MUSIC Algorithm的DoA/AoA估计以及MATLAB实现相关的知识,希望对你有一定的参考价值。
CSI笔记【8】:基于MUSIC Algorithm的DoA/AoA估计以及MATLAB实现
1.DoA/AoA
"AoA":Angle of Arrival,波达角。
"DoA":Direction of Arrival,波达角。
波达方向是指空间信号的到达方向(各个信号到达阵列参考阵元的方向角,简称波大方向),“波达角(AoA)与波达方向(DoA)是同一回事”。
“波达方向(Direction Of Arrival)估计”,又称为“角谱估计(Angle spectral estimation)”、“波达角(Angle Of Arrival)估计”。一个信源有很多可能的传播路径和到达角。如果几个发射机同时工作,每个信源在接收机处形成潜在的多径分量。因此,接收天线能估计出这些到达角就显得很重要,目的是估计出哪个发射机在工作以及发射机所处的方向,简单的说就是利用己方雷达接收来自目标发射机的来波方向进行估计;其物理原理是利用电磁波的直线传播原理。
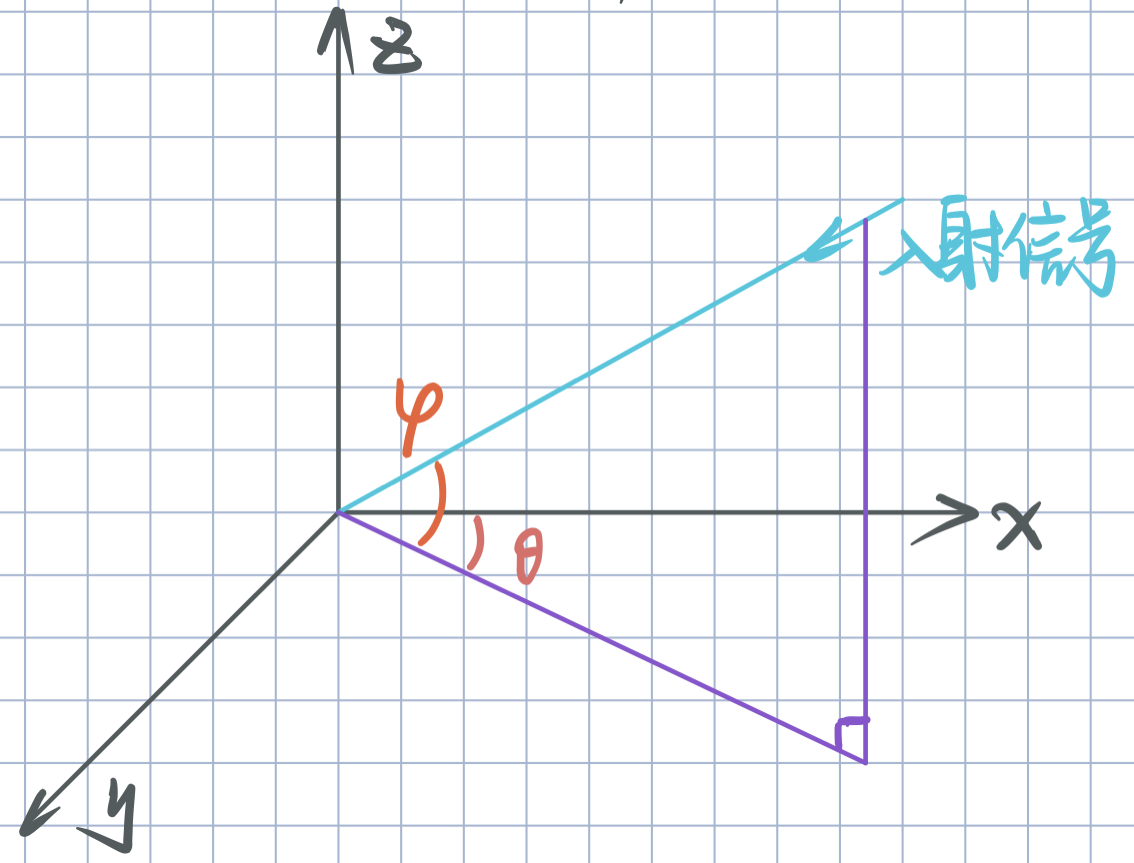
对于 3 D 3D 3D 空间来说, D o A / A o A DoA/AoA DoA/AoA包括 ( θ , ϕ ) (\\theta,\\phi) (θ,ϕ)。对于 2 D 2D 2D 空间来说, D o A DoA DoA 即为方位角 θ \\theta θ。
2.导向向量steering vector
- 导向矢量的本质是描述空间相位差的;
- 导向向量的结构和阵元之间的相对位置有关系。 U L A ULA ULA 的特点是 V a n d e r m o n d e Vandermonde Vandermonde 结构。对于其它集合形状的阵列,导向向量的结构将会有不同。
- 导向向量的值,是来波方向的函数,若 θ \\theta θ 不同,则导向矢量的值会有所不同。
- 对于同一方向 ( e . g . 3 0 ° ) (e.g.\\ 30^{\\degree}) (e.g. 30°) ,若选取的参考点不同,那么导向矢量的值也会不同。但是阵元之间的相对相位差不会变化。
3.MUSIC Algorithm
(1).MUSIC算法概述:
“MUSIC(Multiple Signal Classification,多重信号分类)”,是一类“空间谱估计算法”。其思想是利用接收数据的协方差矩阵进行特征分解,分离出信号子空间和噪声子空间,利用信号“方向向量/导向向量(steering vector)”与噪声子空间的正交性来构成空间扫描谱,进行全域搜索谱峰,从而实现信号的参数估计。
在众多性能优良的高分辨率 D o A DoA DoA 估计算法中, M U S I C MUSIC MUSIC 算法最经典,它在空域内进行谱峰搜索求出信源来向。与最大似然、加权子空间拟合等多维搜索算法相比, M U S I C MUSIC MUSIC 算法运算量要小很多。在 M U S I C MUSIC MUSIC 算法的基础上,发展出了加权 M U S I C MUSIC MUSIC 和改进 M U S I C MUSIC MUSIC 算法等。
M U S I C MUSIC MUSIC 算法建立在一下基础之上:
- 阵列形式为线性均匀阵,阵元间距不大于处理最高频率信号波长的二分之一。
- 信号源个数小于阵元数目,以确保阵列流形矩阵的各个列线性独立。若传感器的数量比信源的个数多,则阵列数据的信号分量一定位于一个低秩的子空间,在一定条件下,这个子空间的将唯一确定信号的波达方向,并且可以使用数值稳定的奇异值分解精确的确定波达方向。
- 处理器的噪声为加性高斯分布,不同阵元间距噪声均为平稳随机过程,各阵元间噪声相互独立,空间平稳(各噪声方差相等)。
- 空间信号为零均值平稳随机过程,信号与阵元噪声相互独立。
- 信号源通常为窄带远场信号。
正是由于 M U S I C MUSIC MUSIC 算法在特定的条件下具有很高的分辨力、估计精度及稳定性,从而吸引了大量的学者对其进行深入的研究和分析。
(2).MUSIC算法原理:
将任意阵列输出数据的协方差矩阵进行特征值分解,对应不同特征值的特征向量构成相互正交的信号子空间和噪声子空间,大特征值对应的特征向量构成的是信号子空间,小特征值对应的特征向量构成的是噪声子空间,然后利用两个子空间之间的正交性来估计信号的方向。
假设
N
N
N 元等距线阵,阵元间距为
d
d
d,信号的波长为
λ
\\lambda
λ,空间中有
N
N
N 个信源,那么接收到的观测信号为:
X
(
t
)
=
∑
i
=
1
N
S
i
(
t
)
A
(
θ
i
)
+
N
(
t
)
X(t)=\\sum_{i=1}^NS_i(t)A(\\theta_i)+N(t)
X(t)=i=1∑NSi(t)A(θi)+N(t)
其中,
S
i
(
t
)
S_i(t)
Si(t) 是第
i
i
i 个信号,
θ
i
\\theta_i
θi 是空间中第
i
i
i 个信号的入射角度。这里假设线性阵列总共接收到
N
N
N 个同源且不相干的信号。
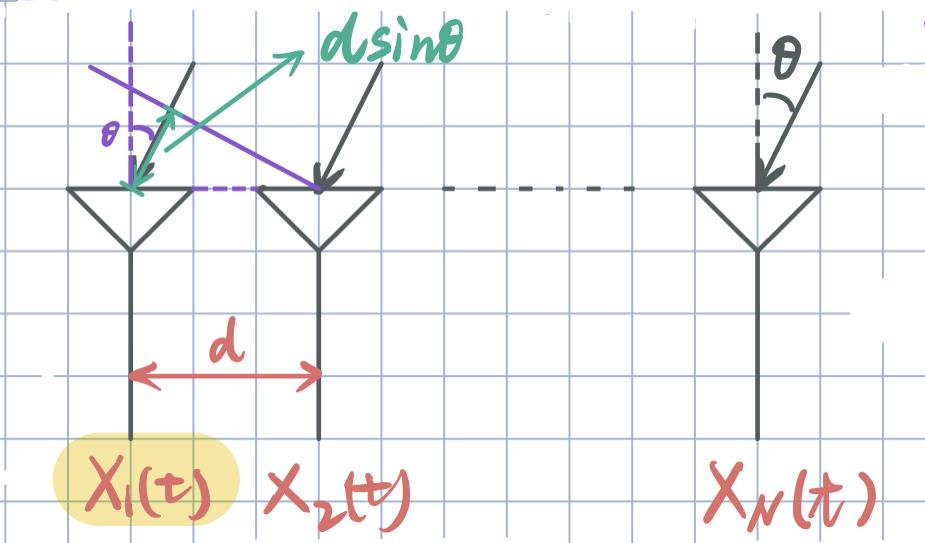
将最左边的天线信道响应作为接受基准,假设为
1
1
1。
所以有:
X
(
t
)
=
A
⋅
S
(
t
)
+
N
(
t
)
A
=
[
A
(
θ
1
)
,
A
(
θ
2
)
,
.
.
.
,
A
(
θ
N
)
]
S
(
t
)
=
[
S
1
(
t
)
,
S
2
(
t
)
,
.
.
.
,
S
N
(
t
)
]
T
X(t)=A\\cdot S(t)+N(t)\\\\ A=[A(\\theta_1),A(\\theta_2),...,A(\\theta_N)]\\\\ S(t)=[S_1(t),S_2(t),...,S_N(t)]^T
X(t)=A⋅S(t)+N(t)A=[A(θ1),A(θ2),...,A(θN)]S(t)=[S1(t),S2(t),...,SN(t)]T
在基于天线阵列协方差矩阵的特征分解类
D
o
A
DoA
DoA 估计算法中,
M
U
S
I
C
MUSIC
MUSIC 算法具有普遍的适用性,只要已知天线阵的布阵形式,无论是线阵还是圆阵,不管阵元是否等间隔分布,都可以得到高分辨率的估计结果。阵列协方差矩阵
R
R
R 可以划分为两个空间,即
R
=
U
S
Σ
S
U
S
H
+
U
N
Σ
N
U
N
H
R=U_S\\Sigma_SU_S^H+U_N\\Sigma_NU_N^H
R=USΣSUSH+UNΣNUNH 。可得
R
U
N
=
A
(
θ
)
R
S
A
H
(
θ
)
U
N
+
σ
n
2
U
N
=
σ
n
2
U
N
(
1
)
RU_N=A(\\theta)R_SA^H(\\theta)U_N+\\sigma^2_nU_N=\\sigma_n^2U_N\\ \\ \\ \\ \\ (1)
RUN=A(θ)RSAH(θ)UN+σn2UN=σn2UN (1)
根据式
(
1
)
(1)
(1)可得
A
(
θ
)
R
S
A
H
(
θ
)
U
N
=
0
(
2
)
A(\\theta)R_SA^H(\\theta)U_N=0\\ \\ \\ \\ \\ (2)
A(θ)RSAH(θ)UN=0 (2)
矩阵
R
S
R_S
RS 为满秩阵,非奇异,所以有逆存在。于是,上式可变为
A
H
(
θ
)
U
N
=
0
A^H(\\theta)U_N=0
AH(θ)UN=0 ,这说明矩阵
A
(
θ
)
A(\\theta)
A(θ) 中的各个列向量与噪声子空间正交,故有
U
N
H
a
(
θ
i
)
=
0
,
i
=
1
,
2
,
.
.
.
,
K
(
3
)
U_N^Ha(\\theta_i)=0,\\ i=1,2,...,K\\ \\ \\ \\ \\ (3)
U《转》笔记3获取csi文件,并用MATLAB处理
技术分享 | 基于 CSI Kubernetes 存储插件的开发实践