动态规划总结

Posted 2021-11-23 tkdz123

1.矩阵连乘问题：

问题描述：
矩阵连乘问题是通过给矩阵连乘时加括号，使得总的计算量最小。

问题分析：

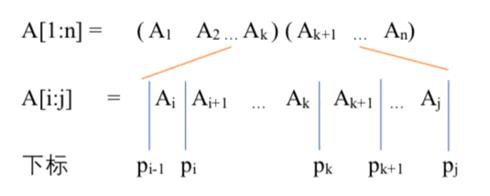
状态转移方程：

 

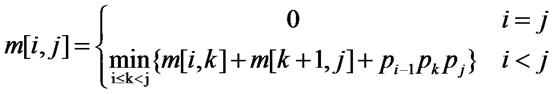
再根据状态转移方程进行填表，右上角即为所求值。

例如，连乘矩阵个数为6，维数分别为：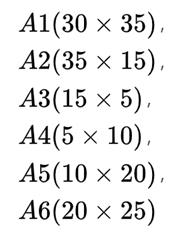

 

填表方式如下图所示：

 

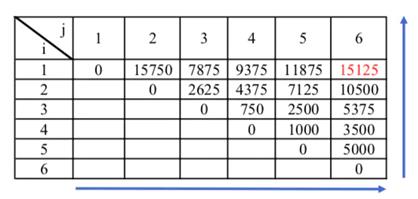
2.最长公共子序列问题：

问题描述： 最长公共子序列，英文缩写为LCS(Longest Common Subsequence)。其定义是，一个序列 S ，如果分别是两个或多个已知序列的子序列，且是所有符合此条件序列中最长的，则 S 称为已知序列的最长公共子序列。

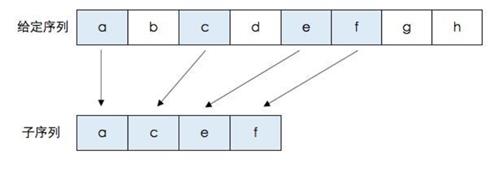
状态转移方程：

f[i,j] = max{f[i-1][j -1] + same(i,j),f[i-1,j],f[i,j-1]}

其中，same(a,b)当 X 的第 a 位与 Y 的第 b 位相同时为"1"，否则为"0"。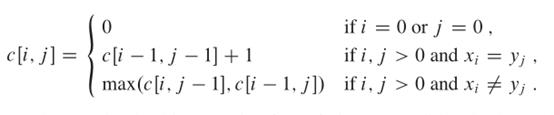

例如求ABCBDAB和BDCABA的LCS

 

灰色且带↖箭头的部分即为所有的LCS的字符

3.最大子段和问题：

题目描述：
给出一段序列，选出其中连续且非空的一段使得这段和最大。

转移方程：dp[i] = max(0, dp[i - 1]) + a[i];

分析：如果说dp[i - 1]小于0，具体些就是以a[i - 1]这个数为结尾的最大子段和小于0的话，那么还不如说就不要前面的数，只留下一个a[i]呢。反之，若dp[i - 1]大于0，那么就让dp[i] = dp[i - 1] + num[i]，这样可以更大些。最后取值为max{dp[i]}

4.凸多边形最优三角剖分：

题目描述：

用多边形顶点的逆时针序列表示凸多边形，即P={v0,v1,…,vn-1}表示具有n条边的凸多边形。

 

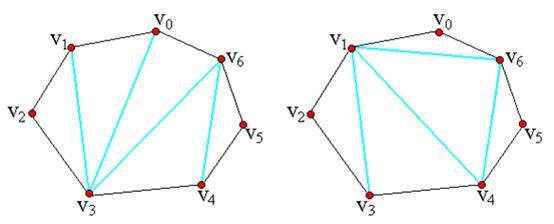
　给定凸多边形P，以及定义在由多边形的边和弦组成的三角形上的权函数w。要求确定该凸多边形的三角剖分，使得即该三角剖分中诸三角形上权之和为最小。

解题思路：

　　若凸(n+1)边形P={v0,v1,…,vn-1}的最优三角剖分T包含三角形v0vkvn，1≤k≤n-1，则T的权为3个部分权的和：三角形v0vkvn的权，子多边形{v0,v1,…,vk}和{vk,vk+1,…,vn}的权之和。可以断言，由T所确定的这2个子多边形的三角剖分也是最优的。因为若有{v0,v1,…,vk}或{vk,vk+1,…,vn}的更小权的三角剖分将导致T不是最优三角剖分的矛盾。

 

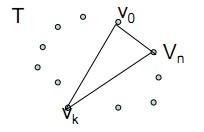
那么我们定义一个t[i][j]，1<=i<=j<=N,为凸子多边形{vi-1,vi,…,vj}的最优三角剖分所对应的权函数值，即其最优值。据此定义，要计算的凸(n+1)边形P的最优权值为t[1][n]。

　　t[i][j]的值可以利用最优子结构性质递归地计算。当j-i≥1时，凸子多边形至少有3个顶点。由最优子结构性质，t[i][j]的值应为t[i][k]的值加上t[k+1][j]的值，再加上三角形vi-1vkvj的权值，其中i≤k≤j-1。由于在计算时还不知道k的确切位置，而k的所有可能位置只有j-i个，因此可以在这j-i个位置中选出使t[i][j]值达到最小的位置。由此，t[i][j]可递归地定义为：

对于要求的t[1][n]，可以用通过由下至上的，从链长（多边形的边）为2开始计算，每次求t[i][j]的最小值，并且记录最小值所对应的K值，根据最优子结构的性质，逐步向上就可以求出t[1][n]的最小值。

类似的，求三角划分顶点的乘积的最小值问题，也是一样的。

5.多边形游戏

给定N个顶点的多边形，每个顶点标有一个整数，每条边上标有+(加)或是×(乘)号，并且N条边按照顺时针依次编号为1~N。

游戏规则 ：(1) 首先，移走一条边。 (2) 然后进行下面的操作： 选中一条边E，该边有两个相邻的顶点，不妨称为V1和V2。对V1和V2顶点所标的整数按照E上所标运算符号(+或是×)进行运算，得到一个整数；用该整数标注一个新顶点，该顶点代替V1和V2 。 持续进行此操作，直到最后没有边存在，即只剩下一个顶点。该顶点的整数称为此次游戏的得分(Score)。

 2、问题分析：

     解决该问题可用动态规划中的最优子结构性质来解。

    设所给的多边形的顶点和边的顺时针序列为op[1],v[1],op[2],v[2],op[3],…,op[n],v[n] 其中，op[i]表示第i条边所对应的运算符，v[i]表示第i个顶点上的数值，i=1~n。

3.最优子结构性质

设所给的多边形的顶点和边的顺时针序列为op[1],v[1],op[2],v[2],op[3],…,op[n],v[n] 其中，op[i]表示第i条边所对应的运算符，v[i]表示第i个顶点上的数值，i=1~n。
       在所给的多边形中，从顶点i（1<=i<=n）开始，长度为j（链中有j个顶点）的顺时针链p(i,j）可表示为v[i],op[i+1],…,v[i+j-1]，如果这条链的最后一次合并运算在op[i+s]处发生（1<=s<=j-1），则可在op[i+s]处将链分割为两个子链p(i,s)和p(i+s,j-s)。
    设m[i,j,0]是链p(i,j)合并的最小值，而m[i,j,1]是最大值。若最优合并在op[i+s]处将p(i,j)分为两个长度小于j的子链的最大值和最小值均已计算出。即：
    a=m[i,s,0]  b=m[i,s,1]  c=m[i+s,j-s,0]  d=m[i+s,j-s,1]

   (1) 当op[i+s]=’+’时
    m[i,j,0]=a+c ；m[i,j,1]=b+d

   该链的最优性由子链的最优性决定，最大值对应于子链的最大值，最小值对应于子链的最小值。

   (2) 当op[i+s]=’*’时
    m[i,j,0]=min{ac,ad,bc,bd} ； m[i,j,1]=max{ac,ad,bc,bd}
   由于v[i]可能取负数，子链的最大值相乘未必能得到主链的最大值，但是注意到，主链的最大值和最小值可以由子链的最大最小值得到。

    由于最优断开位置s有1<=s<=j-1的j-1中情况。 初始边界值为 m[i,1,0]=v[i]   1<=i<=n m[i,1,1]=v[i]   1<=i<=n

可以得到递归表达式，将p(i,j)在op[i+s]处断开的最大值记为maxf(i,j,s)，最小值记为minf(i,j,s)则：

因为多变形式封闭的，在上面的计算中，当i+s>n时，顶点i+s实际编号为(i+s)mod n。按上述递推式计算出的m[i,n,1]记为游戏首次删除第i条边后得到的最大得分。